Lời giải Bài 7 SGK Toán Lớp 10 trang 63 chi tiết nhất

Một bài toán có thể giải bằng rất nhiều phương pháp khác nhau, mỗi phương pháp có ưu điểm, nhược điểm riêng biệt. Dưới đây chúng tôi sẽ hướng dẫn các bạn giải Bài 7 trang 63 SGK Toán 10  bằng cách thức ngắn gọn và chính xác nhất từ đội ngũ chuyên gia môn toán giàu kinh nghiệm.

Giải Bài 7 trang 63 SGK Toán 10:

Giải các phương trình:

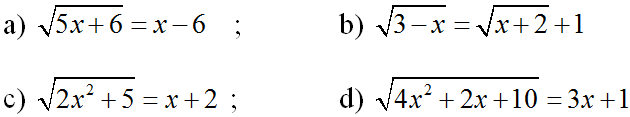
Hướng dẫn giải chi tiết:

a) 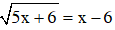 (1)

Điều kiện xác định: 5x + 6 ≥ 0

⇔ 

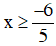
Từ (1) ⇒ 5x + 6 = (x – 6)²

⇔ 5x + 6 = x² – 12x + 36

⇔ x² – 17x + 30 = 0

⇔ (x – 15)(x – 2) = 0

⇔ x = 15 (thỏa mãn ĐKXĐ) hoặc x = 2 (thỏa mãn đkxđ).

Thử lại x = 15 là nghiệm của (1), x = 2 không phải nghiệm của (1)

Vậy phương trình có nghiệm x = 15.

b) 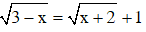(2)

Điều kiện xác định: -2 ≤ x ≤ 3

Ta có (2)

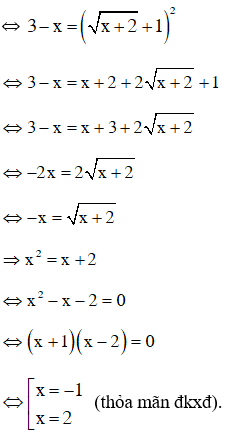
Thử lại thấy x = 2 không phải nghiệm của (2)

Vậy phương trình có nghiệm duy nhất x = –1

c) 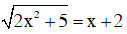(3)

Tập xác định: D = R.

Từ pt (3) ⇒ 2x² + 5 = (x + 2)²

⇔ 2x² + 5 = x² + 4x + 4

⇔ x² – 4x + 1 = 0

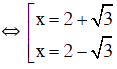
Thử lại ta thấy cả hai giá trị trên đều là nghiệm của (3)

Vậy phương trình có nghiệm là x = 2 + √3; x = 2 - √3.

d) 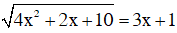(4)

Ta có:

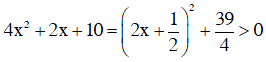
với mọi x.

Do đó phương trình có tập xác định D = R.

Từ (4) ⇒ 4x² + 2x + 10 = (3x + 1)²

⇔ 4x² + 2x + 10 = 9x² + 6x + 1

⇔ 5x² + 4x – 9 = 0

⇔ x = 1 hoặc x = –9/5

Thử lại thấy chỉ có x = 1 là nghiệm của (4)

Vậy phương trình có nghiệm duy nhất x = 1.

Kiến thức áp dụng

+ Để giải các phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương cả hai vế để đưa về một phương trình không chứa ẩn dưới dấu căn.

+ Khi bình phương cả hai vế của một phương trình, ta dùng dấu tương đương khi biết rõ biểu thức ở cả hai vế cùng âm hoặc cùng dương.

Trong trường hợp chưa biết dấu của một trong hai vế hoặc cả hai vế, ta phải dùng dấu suy ra và thử lại nghiệm.

File tải miễn phí Giải Bài 7 trang 63 SGK Toán 10 chi tiết nhất:

Ngoài ra các em có tham khảo thêm nhiều tài liệu ôn tập môn Toán lớp 10 khác như: đề thi, giải bài tập SGK, VBT từ đội ngũ chuyên gia giàu kinh nghiệm chia sẻ miễn phí từ chuyên trang của chúng tôi.