Lời giải Phần Ôn tập chương 2 - Toán lớp 10 chi tiết nhất

Để giúp các em học sinh lớp 10 hệ thống lại toàn bộ kiến thức trọng tâm học trong chương 2, chúng tôi xin giới thiếu Hướng dẫn giải chi tiết Phần Ôn tập chương 2 SGK Toán lớp 10, mời các em học sinh và thầy cô tham khảo dưới đây.

Hướng dẫn giải chi tiết Phần Ôn tập chương 2 - Toán lớp 10

Nội dung lời giải bao gồm các câu hỏi lý thuyết, bài tập ứng dụng phần đại số và hình học.

Ôn tập chương 2 - Phần Đại số

Phần bài tập:

Bài 1 (trang 50 SGK Đại số 10):

Phát biểu quy ước về tập xác định của một hàm số cho bởi công thức.

Từ đó hai hàm số

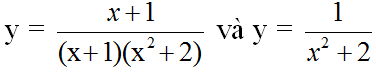
có gì khác nnhau?

Hướng dẫn giải chi tiết:

- Tập xác định của hàm số cho bởi công thức y = f(x) là tập hợp các giá trị của x sao cho biểu thức f(x) có nghĩa.

- Với quy ước đó:

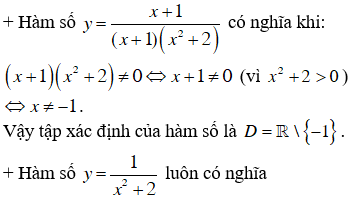
Vậy tập xác định của hàm số là D = R

Kết luận: Hai hàm số 

 

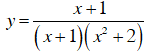
và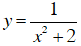 

có tập xác định khác nhau.

Kiến thức áp dụng

+ Hàm phân thức xác định khi mẫu thức khác 0.

+ Hàm căn thức xác định khi biểu thức trong căn ≥ 0.

Bài 2 (trang 50 SGK Đại số 10):

Thế nào là hàm đồng biến (nghịch biến) trên khoảng (a; b) ?

Hướng dẫn giải chi tiết:

Cho hàm số y = f(x) xác định trên khoảng (a; b).

+ Hàm số y = f(x) đồng biến trên khoảng (a; b) nếu:

x1 < x2 ⇔ f(x1) < f(x2) ∀ x1, x2 ∈ (a; b)

+ Hàm số y = f(x) nghịch biến trên khoảng (a; b) nếu:

x1 < x2 ⇔ f(x1) > f(x2) ∀ x1, x2 ∈ (a; b)

Bài 3 (trang 50 SGK Đại số 10):

Thế nào là một hàm số chẵn ? Thế nào là một hàm số lẻ ?

Lời giải:

– Hàm số y = f(x) có tập xác định D được gọi là hàm số chẵn nếu thỏa mãn hai điều kiện:

+ ∀ x ∈ D thì –x ∈ D

+ f(–x) = f(x).

– Hàm số y = f(x) có tập xác định D được gọi là hàm số lẻ nếu thỏa mãn hai điều kiện:

+ ∀ x ∈ D thì –x ∈ D

+ f(–x) = –f(x).

Bài 4 (trang 50 SGK Đại số 10): 

Chỉ ra khoảng đồng biến, nghịch biến của hàm số : y = ax + b, trong mỗi trường hợp a > 0 ; a < 0.

Hướng dẫn giải chi tiết:

- Khi a > 0, hàm số y = ax + b đồng biến trên khoảng (-∞; +∞) hay đồng biến trên R.

- Khi a < 0, hàm số y = ax + b nghịch biến trên khoảng (-∞; +∞) hay nghịch biến trên R.

.........

Lý thuyết Ôn tập chương 2 Đại Số

HÀM SỐ

I. SỰ BIẾN THIÊN CỦA HÀM SỐ

1. Ôn tập

Hàm số y = f(x) gọi là đồng biến (tăng) trên khoảng (a ; b) nếu

∀x1, x2 ∈ (a ; b) : x1 < x2 => f(x1) < f(x2)

Hàm số y = f(x) gọi là nghịch biến (giảm) trên khoảng (a ; b) nếu

2. Bảng biến thiên

Xét chiều biến thiên của một hàm số là tìm các khoảng đồng biến và các khoảng nghịch biến của nó. Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên.

Nhìn vào bảng biến thiên, ta sơ bộ hình dung được đồ thị hàm số (đi lên trong khoảng nào, đi xuống trong khoảng nào).

II. TÍNH CHẴN LẺ CỦA HÀM SỐ

1. Hàm số chẵn, hàm số lẻ

Hàm số với tập xác định gọi là hàm số chẵn nếu

∀x ∈ D thì -x ∈ D và f(x) = f(-x)

Hàm số với tập xác định gọi là hàm số lẻ nếu

∀x1, x2 ∈ (a ; b) : x1 < x2 => f(x1) > f(x2)

2. Đồ thị của hàm số chẵn, hàm số lẻ

Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.

Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.

HÀM SỐ y = ax + b

I. ÔN TẬP VỀ HÀM SỐ BẬC NHẤT

y = ax + b ( a ≠ 0 ).

Tập xác định D = R

Chiều biến thiên

Với a > 0 hàm số đồng biến trên

Với a < 0 hàm số nghịch biến trên

Bảng biến thiên

.............................

Ôn tập chương 2 - Phần Hình học

Phần bài tập:

Bài 1 (trang 62 SGK Hình học 10):

Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?

Hướng dẫn giải chi tiết:

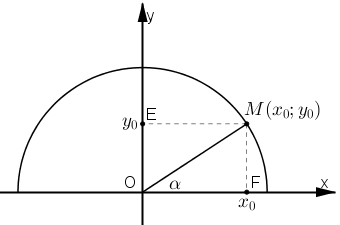
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho 

Khi đó ta có:

sin α = y0

cos α = x0

tan α = y0 / x0

cot α = x0 / y0

b) Gọi E, F là hình chiếu của M trên Oy, Ox.

Khi α < 90º thì x0 > 0, y0 > 0

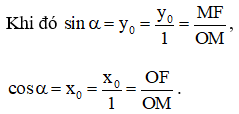
Bài 2 (trang 62 SGK Hình học 10): 

Tại sao hai góc bù nhau lại có sin bằng nhau và coossin đối nhau?

Hướng dẫn giải chi tiết:

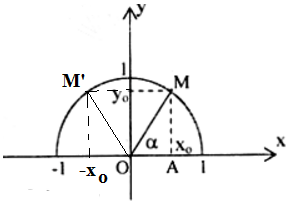
Gọi M(xo; yo) nằm trên nửa đường tròn đơn vị sao cho ∠xOM = α

Khi đó điểm M'(-xo; yo) trên nửa đường tròn đơn vị sao cho ∠xOM' = 180o - α (tức là ∠xOM' là bù với ∠xOM = α)

Do đó: 

sinα = yo = sin(180o - α)

cosα = xo = -(-xo) = -cos(180o - α)

Bài 3 (trang 62 SGK Hình học 10): 

Nhắc lại định nghĩa tích vô hướng của hai vectơ a→ và b→. Tích vô hướng này với |a→| và |b→| không đổi đạt giá trị lớn nhất và nhỏ nhất khi nào?

Hướng dẫn giải chi tiết:

Tích vô hướng của hai vec tơ a→ và b→:

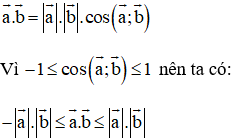
+ a→.b→ đạt giá trị lớn nhất bằng 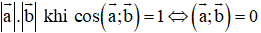 ⇔ a→ và b→ cùng hướng.

+ a→.b→ đạt giá trị nhỏ nhất bằng 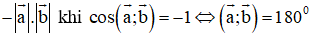⇔ a→ và b→ ngược hướng.

..............

Lý thuyết tổng hợp chương 2 - Hình học:

Giá trị lượng giác của một góc bất kì từ 0o đến 180o

1. Tính chất

Trên hình bên ta có dây cung NM song song với trục Ox và nếu ∠ xOM = α thì ∠xON = 180o – α. Ta có yM = yN = yo, xM = –xN = xo. Do đó

sin α = sin(180o – α)

cos α = –cos(180o – α)

tan α = –tan(180o – α)

cot α = –cot(180o – α)

2. Giá trị lượng giác của các góc đặc biệt

Trong bảng kí hiệu “||” để chỉ giá trị lượng giác không xác định.

Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.

Chẳng hạn:

sin 120o = sin(180o – 60o) = sin60o 

...............

File tải bản đầy đủ hướng dẫn giải chi tiết Phần Ôn tập chương 2 - Toán lớp 10:

Chúc các em thành công!