Hướng dẫn giải bài tập toán hình 11 trang 59 chi tiết nhất

Để quá trình tiếp thu kiến thức mới trở nên dễ dàng và đạt hiệu quả nhất, trước khi bắt đầu bài học mới các em cần có sự chuẩn bị nhất định qua việc tổng hợp nội dung kiến thức lý thuyết trọng tâm, sử dụng những kiến thức hiện có thử áp dụng giải các bài toán, trả lời câu hỏi liên quan. Dưới đây chúng tôi đã soạn sẵn Lời giải Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song SGK trang 59 đầy đủ nhất, giúp các em tiết kiệm thời gian. Nội dung chi tiết được chia sẻ dưới đây.

Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Trả lời câu hỏi ứng dụng:

Câu hỏi trang 55:

Quan sát các cạnh tường trong lớp học và xem cạnh tường là hình ảnh của đường thẳng. Hãy chỉ ra một số cặp đường thẳng không thể cùng thuộc một mặt phẳng.

Hướng dẫn giải chi tiết:

Học sinh tự quan sát

Câu hỏi trang 56:

Cho tứ diện ABCD, chứng minh hai đường thẳng AB và CD chéo nhau. Chỉ ra cặp đường thẳng chéo nhau khác của tứ diện này (h.2.29).

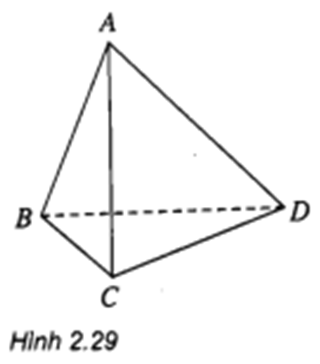
Hướng dẫn giải chi tiết:

Không tìm được mặt phẳng nào chứa AB và CD ⇒ AB và CD chéo nhau

Các cặp đường thẳng chéo nhau khác của tứ diện này: AC và BD, BC và AD

Câu hỏi trang 57:

Cho hai mặt phẳng α và β. Một mặt phẳng λ cắt α và β lần lượt theo các giao tuyến a và b. Chứng minh rằng khi a và b cắt nhau tại I thì I là điểm chung của α và β. (h.2.32).

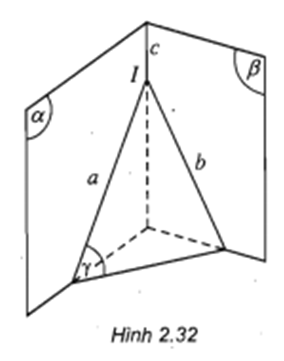
Hướng dẫn giải chi tiết:

a và b cắt nhau tại I

I ∈ a ∈ α (vì a là giao tuyến của α và λ)

I ∈ b ∈ β ( vì b là giao tuyến của β và λ)

Nên I là điểm chung của α và β

Bài tập ứng dụng:

Bài 1 (trang 59 SGK Hình học 11): 

Cho tứ diện ABCD. Gọi P, Q, R và S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD và DA. Chứng minh rằng nếu bốn điểm P, Q, R và S đồng phẳng thì:

a) Ba đường thẳng PQ, SR và AC hoặc song song hoặc đồng quy.

b) Ba đường thẳng PS, RQ và BD hoặc song song hoặc đồng quy.

Phương pháp giải:

Sử dụng định lí 2 (về giao tuyến của ba mặt phẳng):

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

Hướng dẫn giải chi tiết:

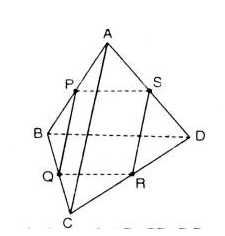
a) Ta có:

PQ = (ABC) ∩ (PQRS)

RS = (PQRS) ∩ (ACD)

AC = (ABC) ∩ (ACD)

Vậy hoặc PQ, RS, AC đồng qui hoặc song song.

b) PS =(ABD) ∩ (PQRS)

RQ = (BCD) ∩ (PQRS)

BD = (ABD) ∩ (CBD)

Vậy PS, RQ, BD đồng quy hoặc song song.

Kiến thức áp dụng

+ Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc song song với nhau hoặc đồng quy.

Bài 2 (trang 59 SGK Hình học 11): 

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Tìm giao điểm S của AD và mặt phẳng (PQR) trong hai trường hợp sau đây.

a) PR song song với AC;

b) PR cắt AC.

Hướng dẫn giải chi tiết:

a) PR // AC

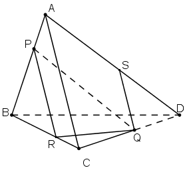
mp(PQR) và mp(ACD) lần lượt chứa hai đường thẳng song song PR // AC

⇒ (PQR) ∩ (ACD) = Qt là đường thẳng song song với AC và PR.

Gọi Qt ∩ AD = S

⇒ S = AD ∩ (PQR).

b) PR ∩ AC = I.

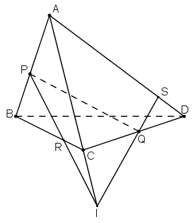
Có : Q ∈ (ACD) ∩ (PQR)

+ (ABC) ∩ (PQR) = PR.

+ (ACD) ∩ (ABC) = AC

+ (ACD) cắt (PQR)

⇒ PR; AC và giao tuyến của (ACD) và (PQR) đồng quy

Mà PR ∩ AC = I

⇒ I ∈ (ACD) ∩ (PQR).

⇒ (ACD) ∩ (PQR) = QI.

trong (ACD): QI ∩ AD = S chính là giao tuyến của (PQR) và AD.

Kiến thức áp dụng

+ Nếu ba mặt phẳng cắt nhau đôi một theo ba giao tuyến phân biệt thì ba giao tuyến ấy song song hoặc đồng quy.

+ Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sẽ song song hoặc trùng với một trong hai đường thẳng đó.  

Bài 3 (trang 60 SGK Hình học 11): 

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.

a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).

b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.

c) Chứng minh GA = 3GA’

Hướng dẫn giải chi tiết:

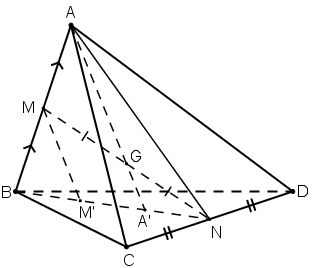
a) Có: MN ⊂ (ABN)

⇒ G ∈ (ABN)

⇒ AG ⊂ (ABN).

Trong (ABN), gọi A’ = AG ∩ BN.

⇒ A’ ∈ BN ⊂ (BCD)

⇒ A’ = AG ∩ (BCD).

b)

+ Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)

⇒ Mx ⊂ (ABN).

M’ = Mx ∩ (BCD)

⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.

⇒ B; M’; A’ thẳng hàng.

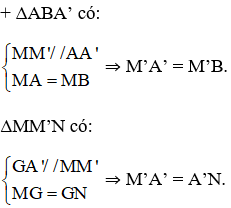
⇒ BM’ = M’A’ = A’N.

c) Áp dụng chứng minh câu b ta có:

ΔMM’N có: MM’ = 2.GA’

ΔBAA’ có: AA’ = 2.MM’

⇒ AA’ = 4.GA’

⇒ GA = 3.GA’.

Lý thuyết trọng tâm:

1. Vị trí tương đối của hai đường thẳng phân biệt

    Cho hai đường thẳng a và b. Căn cứ vào sự đồng phẳng và số điểm chung của hai đường thẳng ta có bốn trường hợp sau:

    a. Hai đường thẳng song song: cùng nằm trong một mặt phẳng và không có điểm chung, tức là

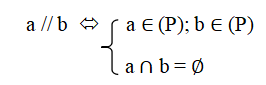
     b. Hai đường thẳng cắt nhau: chỉ có một điểm chung.

        a cắt b khi và chỉ khi a ⋂ b = I.

     c. Hai đường thẳng trùng nhau: có hai điểm chung phân biệt.

        a ⋂ b = {A, B} ⇔ A ≡ B

     d. Hai đường thẳng chéo nhau: không cùng thuộc một mặt phẳng.

        a chéo b khi và chỉ khi a, b không đồng phẳng.

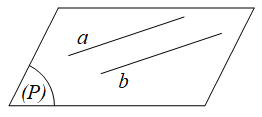
        a song song với b

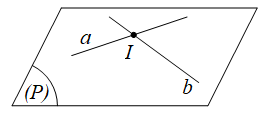
        a cắt b tại giao điểm I

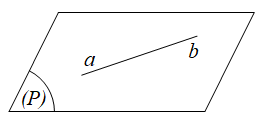
        a và b cắt nhau tại vô số điểm (trùng)

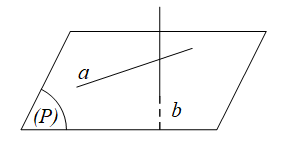
        a và b chéo nhau

2. Hai đường thẳng song song

Tính chất 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.

Tính chất 2: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

Định lí: (về giao tuyến của hai mặt phẳng): Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Hệ quả: Nếu hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).

File tải miễn phí hướng dẫn soạn - Toán Hình 11 trang 59 Bài 2:

Hy vọng tài liệu sẽ hữu ích cho các em học sinh và quý thầy cô tham khảo và đối chiếu đáp án chính xác.

►Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích hỗ trợ ôn luyện thi môn toán như đề kiểm tra, hướng dẫn giải sách giáo khoa, vở bài tập được cập nhật liên tục tại chuyên trang của chúng tôi.