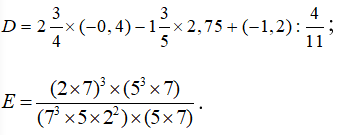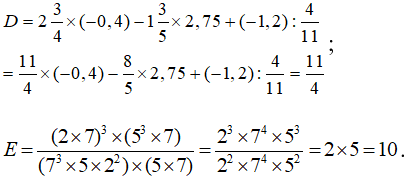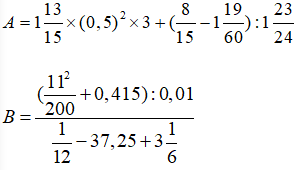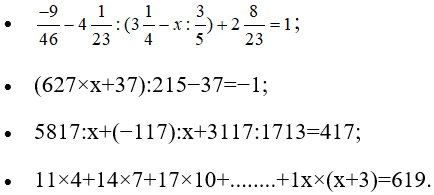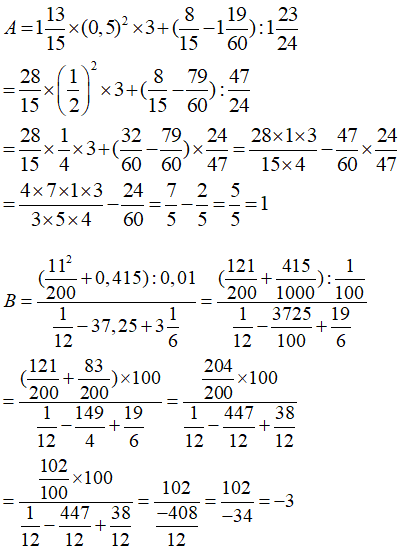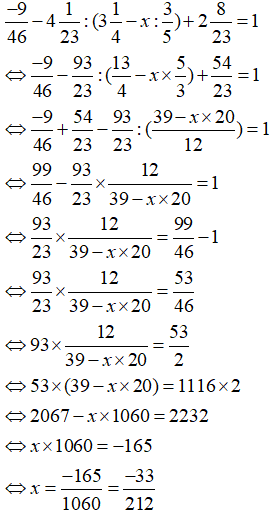Giải Bài 20: Ôn tập cuối năm Toán VNEN lớp 6
Hướng dẫn giải bài tập Toán lớp 6 VNEN Bài 20: Ôn tập cuối năm chi tiết, dễ hiểu được biên soạn bởi đội ngũ chuyên gia giàu kinh nghiệm chia sẻ. Hy vọng đây sẽ là tài liệu hữu ích hỗ trợ học sinh trong quá trình học tập. Mời các em tham khảo tại đây.
Giải Toán 6 VNEN Bài 20: Hoạt động luyện tập
I. Ôn tập lý thuyết
Câu 1 (Trang 65 Toán VNEN 6 tập 2)
a) Em đọc các kí hiệu ∈;∉;⊂;∩;∅
Em viết một số ví dụ có sử dụng kí hiệu trên.
b) Điền vào chỗ trống
c) Điền vào bảng sau
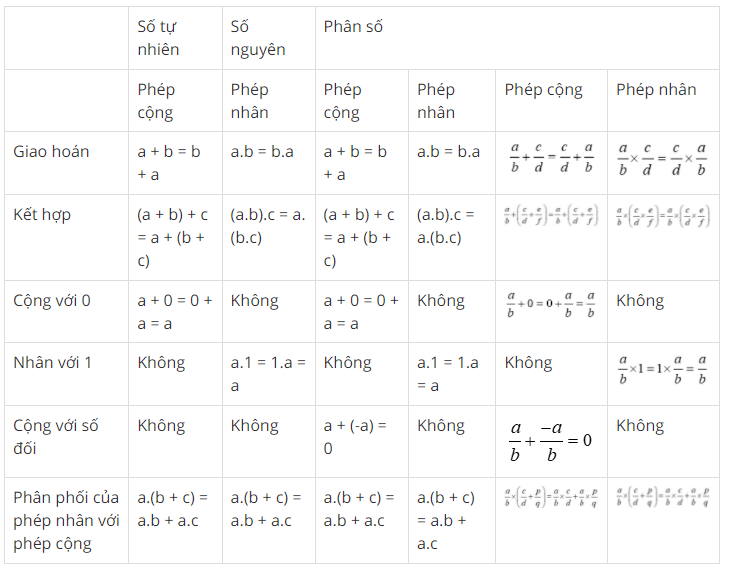
So sánh các tính chất cơ bản của phép cộng và phép nhân số tự nhiên, số nguyên, phân số.
|
| Số tự nhiên | Số nguyên | Phân số | |||
|
| Phép cộng | Phép nhân | Phép cộng | Phép nhân | Phép cộng | Phép nhân |
| Giao hoán | a + b = b + a |
|
|
|
| |
| Kết hợp |
|
|
|
|
|
|
| Cộng với 0 |
|
|
|
|
|
|
| Nhân với 1 |
|
|
|
|
|
|
| Cộng với số đối |
|
|
|
|
|
|
| Phân phối của phép nhân với phép cộng |
|
|
|
|
|
|
Lời giải:
a) Tên của các kí hiệu ∈;∉;⊂;∩;∅ lần lượt là: thuộc, không thuộc, tập con, giao, rỗng.
Ví dụ: Cho tập hợp A = {1, 2, 3, 4, 5}
• 1 ∈ A;
• 6 ∉ A;
• B = {1, 2} ⊂ A;
• Cho C = {1, 3, 6, 9} thì A ∩ C={1,3};
• Cho tập D không có phần tử nào, vậy D = {∅}
b)
c)
Câu 2 (Trang 65 Toán VNEN 6 tập 2)
Hãy điền từ tích hợp vào chỗ trống trong bảng so sánh tìm ƯCLN và BCNN của hai hay nhiều số.
| Cách tìm | ƯCLN | BCNN |
| Phân tích ra các thừa số nguyên tố |
|
|
| Xét các thừa số nguyên tố | .............. | .............. |
| Lập tích các thừa số nguyên tố đó, mỗi thừa số lấy với số mũ | .............. | .............. |
Lời giải:
| Cách tìm | ƯCLN | BCNN |
| Phân tích ra các thừa số nguyên tố |
|
|
| Xét các thừa số nguyên tố | chung | chung và riêng |
| Lập tích các thừa số nguyên tố đó, mỗi thừa số lấy với số mũ | nhỏ nhất | lớn nhất |
II. Bài tập
Câu 1 (Trang 66 Toán VNEN 6 tập 2)
a) Điền các kí hiệu: ∈;∉;⊂;∩;∅ thích hợp vào chỗ trống
−34 ... Z;
0 ... N
3,275 ... N
-13 ... Z
N .... Z = N
N ... Z
b) Điền vào chỗ trống
Cho tập C là tập hợp các số chẵn, tập L là tập hợp các số lẻ, khi đó C ∩ L=....
Lời giải:
a)
−34 ∉ Z;
0 ∈ N
3,275 ∉ N
-13 ∈ Z
N ∩ Z = N
N ⊂ Z
b) C ∩ L = ∅
Câu 2 (Trang 66 Toán VNEN 6 tập 2)
a) Tính giá trị của các biểu thức sau:
A = 23 + 36 + 79 + 44 + 57;
B = -277 - (98 - 377);
C = -1,4 x 2,3 + 1,4 x (-3,7) - 1,4 x 3 - 0,14 x 0,1;
b) Chia đều 50 chiếc kẹo cho tất cả học sinh lớp 6C, mỗi em được số kẹo là một số tự nhiên thì còn dư 12 chiếc. Hỏi lớp 6C có bao nhiêu học sinh (biết mỗi bạn được chia nhiều hơn 1 chiếc kẹo)?
c) Một ca nô xuôi một khúc sông hết 3 giờ và ngược khúc sông đó hết 5 giờ. Biết vận tốc dòng nước là 3 km/h. Tính chiều dài khúc sông đó.
Lời giải:
a)
A = 23 + 36 + 79 + 44 + 57 = (23 + 57) + (36 + 44) + 79
= 80 + 80 + 79 = 160 + 79 = 239;
B = -277 - (98 - 377) = -277 - 98 + 377 = (377 - 277) - 98 = 100 - 98 = 2;
C = -1,4 x 2,3 + 1,4 x (-3,7) - 1,4 x 3 - 0,14 x 0,1
= -1,4 x 2,3 + 1,4 x (-3,7) - 1,4 x 3 - 1,4 x 0,01
= 1,4 x [(-2,3) - 3,7 - 3 - 0,01]
= 1,4 x [-6 - 3 - 0,01]
= 14 x (-9,01)
= -12,614;
b) Số kẹo dùng để chia cho lớp 6C là: 50 - 12 = 38.
Vì 38 chia hết cho số học sinh của lớp 6C nên số học sinh lớp 6C là Ư(38) (Ước nguyên dương).
Ư(38) = {1, 2, 19, 38}.
Vì mỗi bạn được nhiều hơn 1 chiếc kẹo, nên số học sinh lớp 6C có thể là 1, 2, 19.
Thông thường, lớp học ở Việt Nam có số học sinh > 10. Vậy số học sinh lớp 6C hợp lý là: 19 học sinh.
c) Gọi vận tốc thực của cano là x (km/h)
Suy ra, vận tốc cano khi xuôi dòng là x + 3 (km/h), vận tốc cano khi ngược dòng là x - 3 (km/h).
Độ dài khúc sông khi đi xuôi dòng và khi đi ngược dòng là không thay đổi:
(x + 3) × 3 = (x − 3) × 5
⇔ 5x − 3x = 9 + 15
⇔ 2x = 24
⇔ x = 12 (km/h).
Vậy độ dài khúc sông là: S = (x + 3) × 3 = (12 + 3) × 3 = 45 km.
Câu 3 (Trang 67 Toán VNEN 6 tập 2)
a) Tính
b) Tìm x, biết:
c) Hai vòi nước cùng chảy vào một bể cạn. Biết rằng để chảy được 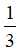
d) So sánh hai biểu thức A và B, biết rằng:
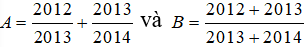
Lời giải:
a)
b)
c)
d)
Giải Toán VNEN lớp 6 Bài 20: Hoạt động vận dụng
"Tỉ số vàng" (đọc thêm sgk).
a) Các kích thước của một hình chữ nhật tuân theo "Tỉ số vàng", biết rằng chiều rộng của nó đo được là 3,09 m. Tính chiều dài của hình chữ nhật đó.
b) Chiều dài của hình chữ nhật là 4,5 m. Để có "Tỉ số vàng" thì chiều rộng của nó phải bằng bao nhiêu.
c) Một khu vườn hình chữ nhật có chiều dài là 15,4 m, chiều rộng là 8 m. Khu vườn này có đạt "Tỉ số vàng" không?
Lời giải:
a) Chiều dài của hình chữ nhật là: x : 3,09 = 1 : 0,618 ⇒ x = (1:0,618) × 3,09 = 5 m.
b) Chiều rộng khu vườn là: 4,5 : x = 1 : 0,618 ⇒ x = 4,5:(1:0,618) = 2,781 m.
c) Tỉ số giữa chiều dài và chiều rộng là: 15,4 : 8 = 1 : 0,519. Đây không phải tỉ số vàng.
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán lớp 6 sách VNEN Tập 2 Bài 20: Ôn tập cuối năm file PDF hoàn toàn miễn phí.
- Giải Bài 5: Thực hành đo góc trên mặt đất Toán VNEN lớp 6
- Giải Bài 7: Ôn tập chương 2 Toán VNEN lớp 6
- Giải Bài 4: Quy đồng mẫu nhiều phân số - Luyện tập Toán VNEN lớp 6
- Giải Bài 13: Luyện tập chung Toán VNEN lớp 6
- Giải Bài 18: Biểu đồ phần trăm - Luyện tập Toán VNEN lớp 6
- Giải Bài 6: Đường tròn - tam giác Toán VNEN lớp 6
- Giải Bài 15: Tìm một số biết giá trị phân số của số đó - Luyện tập Toán VNEN lớp 6
- Giải Bài 8: Phép trừ phân số - Luyện tập Toán VNEN lớp 6