Giải bài tập Toán lớp 6 Bài 3: So sánh phân số Chân trời sáng tạo
Mời các em học sinh và quý thầy cô tham khảo ngay hướng dẫn Giải bài tập Toán 6 Bài 3: So sánh phân số Chân trời sáng tạo (chính xác nhất) được đội ngũ chuyên gia biên soạn ngắn gọn và đầy đủ, có đáp án chi tiết cho từng bài tập giúp các em học sinh ôn tập những dạng bài để học tốt được môn Toán lớp 6. Mời các em cùng tham khảo chi tiết dưới đây.
Trả lời câu hỏi SGK Bài 3 Toán lớp 6 Chân trời sáng tạo
Hoạt động khám phá 1 trang 13 Toán lớp 6 Tập 2: Do dịch bệnh Covid-19, trung bình mỗi tháng trong 3 tháng cuối năm 2020, công ty A đạt lợi nhuận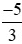 tỉ đồng, công ty B đạt lợi nhuận
tỉ đồng, công ty B đạt lợi nhuận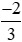 tỉ đồng. Công ty nào đạt lợi nhuận ít hơn?
tỉ đồng. Công ty nào đạt lợi nhuận ít hơn?
Lời giải:
Công ty A đạt lợi nhuận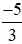 tỉ đồng có nghĩa là công ty A lỗ
tỉ đồng có nghĩa là công ty A lỗ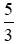 tỉ đồng.
tỉ đồng.
Công ty B đạt lợi nhuận tỉ đồng có nghĩa là công ty B lỗ
tỉ đồng có nghĩa là công ty B lỗ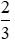 tỉ đồng.
tỉ đồng.
Vì 5 > 2 nên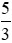 >
> 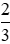 .
.
Do đó công ty A sẽ lỗ nhiều hơn công ty B.
Vậy lợi nhuận công ty A đạt được ít hơn công ty B.
Thực hành 1 trang 13 Toán lớp 6 Tập 2: So sánh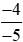 và
và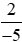 .
.
Lời giải:
Đưa hai phân số về cùng mẫu dương, ta được:
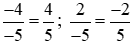 .
.
Do 4 > −2 nên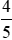 >
>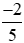 .
.
Vậy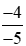 >
> 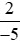 .
.
Hoạt động khám phá 2 trang 13 Toán lớp 6 Tập 2: Đưa hai phân số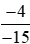 và
và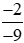 về dạng hai phân số có mẫu dương rồi quy đồng mẫu của chúng.
về dạng hai phân số có mẫu dương rồi quy đồng mẫu của chúng.
Lời giải:
- Đưa hai phân số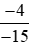 và
và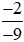 về cùng mẫu dương, ta được:
về cùng mẫu dương, ta được:
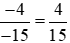 và
và 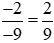 .
.
- Quy đồng mẫu số hai phân số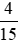 và
và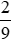 , ta được:
, ta được:
Mẫu số chung: 45.
Ta thực hiện: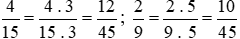 .
.
Thực hành 2 trang 14 Toán lớp 6 Tập 2:
So sánh: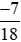 và
và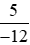 .
.
Lời giải:
Mẫu số chung của hai hay nhiều phân số là số chia hết cho tất cả các mẫu số của các phân số đó.
Ta thường để mẫu số chung là bội chung nhỏ nhất của các số ở mẫu để các phân số sau khi quy đồng sẽ đơn giản nhất có thể.
Ta có: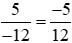
* Quy đồng hai phân số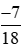 và
và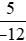 .
.
Mẫu số chung: 36.
Ta thực hiện: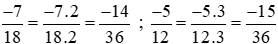 .
.
Vì –14 > –15 nên 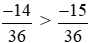
Do đó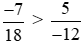 .
.
Vậy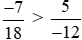 .
.
Thực hành 3 trang 14 Toán lớp 6 Tập 2: Viết số nguyên dưới dạng phân số rồi so sánh.
a)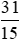 và 2;
và 2;
b) −3 và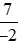 .
.
Lời giải:
a) Ta có: 2 =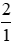 .
.
Mẫu số chung: 15.
Ta thực hiện: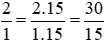 và giữ nguyên phân số
và giữ nguyên phân số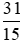 .
.
Vì 31 > 30 nên 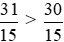 .
.
Do đó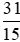 > 2.
> 2.
Vậy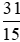 > 2.
> 2.
b) −3 và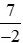
Ta có: −3 =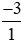 ;
;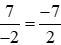 .
.
Mẫu số chung: 2.
Ta thực hiện: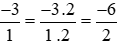 và giữ nguyên phân số
và giữ nguyên phân số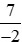 .
.
Vì −6 > −7 nên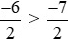
Do đó −3 >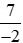 .
.
Vậy −3 >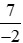 .
.
Hoạt động khám phá 3 trang 14 Toán lớp 6 Tập 2: Thực hiện quy đồng mẫu số ba phân số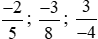 rồi sắp xếp các phân số đó theo thứ tự tăng dần.
rồi sắp xếp các phân số đó theo thứ tự tăng dần.
Lời giải:
Ta có: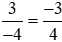 .
.
* Quy đồng mẫu số ba phân số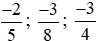 .
.
Mẫu số chung: 40.
Ta thực hiện: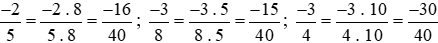 .
.
Vì −30 < −16 < −15 nên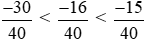 .
.
Do đó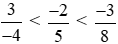
Vậy các phân số được sắp xếp theo thứ tự tăng dần là: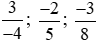 .
.
Thực hành 4 trang 14 Toán lớp 6 Tập 2: So sánh:
a)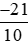 và 0;
và 0;
b) 0 và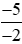 ;
;
c)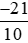 và
và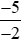 .
.
Lời giải:
a) Phân số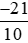 là phép chia −21 cho 10, có −21 là số âm và 10 là số dương nên thương của phép chia này là một số âm.
là phép chia −21 cho 10, có −21 là số âm và 10 là số dương nên thương của phép chia này là một số âm.
Do đó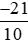 < 0.
< 0.
b) Phân số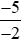 là phép chia −5 cho −2, có −5 là số âm và −2 là số âm nên thương của phép chia này là một số dương.
là phép chia −5 cho −2, có −5 là số âm và −2 là số âm nên thương của phép chia này là một số dương.
Do đó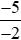 > 0.
> 0.
c) Từ câu a và câu b, ta có: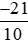 < 0 và 0 <
< 0 và 0 < 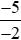 .
.
Theo tính chất bắc cầu, ta suy ra:
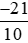 <
<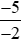 .
.
* Nhận xét:
- Phân số có tử số và mẫu số cùng dấu thì phân số lớn hơn 0 và phân số đó gọi là phân số dương.
- Phân số có tử số và mẫu số trái dấu thì phân số nhỏ hơn 0 và phân số đó gọi là phân số âm.
- Phân số dương luôn lớn hơn phân số âm (vì áp dụng tính chất bắc cầu: phân số dương luôn lớn hơn 0, phân số âm luôn nhỏ hơn 0).
Vận dụng trang 14 Toán lớp 6 Tập 2: Bạn Nam rất thích ăn sô cô la. Mẹ Nam có một thanh sô cô la, mẹ cho Nam chọn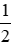 hoặc
hoặc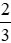 thanh sô cô la đó. Theo em bạn Nam sẽ chọn phần nào?
thanh sô cô la đó. Theo em bạn Nam sẽ chọn phần nào?
Lời giải:
Quy đồng hai phân số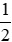 và
và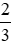 , ta được:
, ta được:
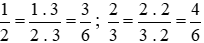 .
.
Vì 3 < 4 nên 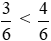 hay
hay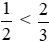 .
.
Bạn Nam rất thích ăn sô cô la nên rất có thể bạn Nam sẽ chọn phần nhiều hơn.
Vậy theo em, bạn Nam sẽ chọn phần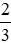 thanh sô cô la.
thanh sô cô la.
Giải bài tập SGK Toán 6 Chân trời sáng tạo Bài 3
Bài 1 trang 15 Toán lớp 6 Tập 2: So sánh hai phân số.
a)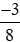 và
và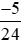 ;
;
b)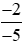 và
và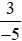 ;
;
c)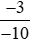 và
và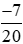 ;
;
d)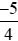 và
và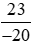 .
.
Lời giải:
a)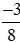 và.
và.
Mẫu số chung: 24.
Ta thực hiện: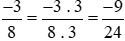 và giữ nguyên phân số
và giữ nguyên phân số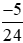 .
.
Vì −9 < −5 nên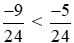 .
.
Do đó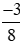 <
<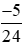 .
.
Vậy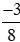 <
<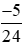 .
.
b)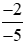 và
và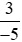
Cách 1: (Đưa hai phân số về cùng mẫu dương rồi so sánh tử số của hai phân số đó).
Đưa hai phân số về cùng mẫu dương, ta được:
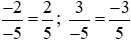
Vì −2 > −3 nên 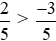
Vậy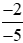 >
>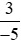 .
.
Cách 2: (So sánh hai phân số đó với 0 và áp dụng tính chất bắc cầu).
Ta có: 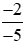 > 0 (phân số có tử số và mẫu số cùng dấu)
> 0 (phân số có tử số và mẫu số cùng dấu)
Và 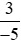 < 0 (phân số có tử số và mẫu số trái dấu).
< 0 (phân số có tử số và mẫu số trái dấu).
Áp dụng tính chất bắc cầu, ta suy ra: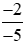 >
>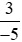 .
.
Vậy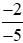 >
>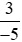 .
.
c)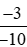 và
và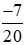
Cách 1: (Đưa hai phân số về cùng mẫu dương rồi so sánh tử số của hai phân số đó).
Ta có: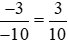 .
.
Mẫu số chung của hai phân số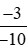 và
và 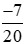 là 20.
là 20.
Ta thực hiện: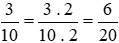 và
và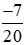 .
.
Vì 6 > −7 nên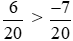 hay
hay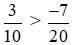 .
.
Vậy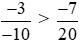 .
.
Cách 2: (So sánh hai phân số đó với 0 và áp dụng tính chất bắc cầu).
Ta có: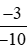 > 0 (phân số có tử số và mẫu số cùng dấu)
> 0 (phân số có tử số và mẫu số cùng dấu)
Và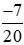 < 0 (phân số có tử số và mẫu số trái dấu).
< 0 (phân số có tử số và mẫu số trái dấu).
Áp dụng tính chất bắc cầu, ta suy ra: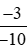 >
>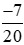 .
.
Vậy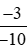 >
>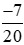 .
.
d)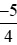 và
và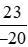
Ta có: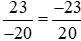
Mẫu số chung của hai phân số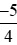 và
và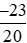 là 20.
là 20.
Ta thực hiện: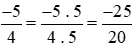 và giữ nguyên phân số
và giữ nguyên phân số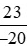 .
.
Vì −25 < −23 nên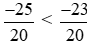 hay
hay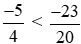 .
.
Vậy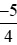 <
<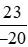 .
.
Bài 2 trang 15 Toán lớp 6 Tập 2: Tổ 1 gồm 8 bạn có tổng chiều cao là 115 dm. Tổ 2 gồm 10 bạn có tổng chiều cao là 138 dm. Hỏi chiều cao trung bình của các bạn ở tổ nào lớn hơn?
Lời giải:
Trung bình chiều cao của mỗi bạn ở tổ 1 là:
115 : 8 = 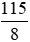 (dm)
(dm)
Trung bình chiều cao của mỗi bạn ở tổ 2 là:
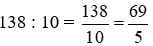 (dm)
(dm)
Ta có: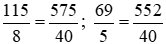 .
.
Vì 575 > 552 nên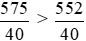 hay
hay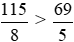 .
.
Vậy chiều cao trung bình của các bạn tổ 1 lớn hơn.
Bài 3 trang 15 Toán lớp 6 Tập 2: a) So sánh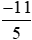 với
với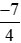 với –2 bằng cách viết –2 ở dạng phân số có mẫu số thích hợp.
với –2 bằng cách viết –2 ở dạng phân số có mẫu số thích hợp.
Từ đó suy ra kết quả so sánh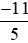 với
với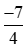 .
.
b) So sánh 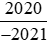 với
với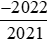 .
.
Lời giải:
a) Ta có: −2 =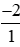 .
.
Mẫu số thích hợp để so sánh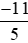 với
với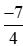 với –2 là mẫu số chung của ba phân số
với –2 là mẫu số chung của ba phân số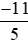 ;
;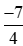 và −2 (ta nên tìm mẫu chung nhỏ nhất để phân số sau khi quy đồng đơn giản nhất có thể).
và −2 (ta nên tìm mẫu chung nhỏ nhất để phân số sau khi quy đồng đơn giản nhất có thể).
Mẫu số chung là 20.
Ta thực hiện:
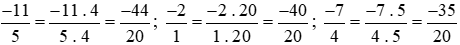
Vì −44 < −40 nên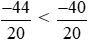 hay
hay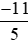 < −2.
< −2.
Vì −40 < −35 nên 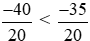 hay −2 <
hay −2 <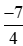 .
.
Áp dụng tính chất bắc cầu, ta suy ra: < .
Vậy 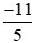 <
<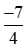 .
.
b) So sánh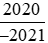 với
với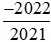 .
.
Nhận thấy: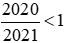 và
và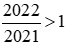 .
.
Do đó để so sánh hai phân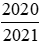 và
và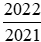 , ta có thể so sánh chúng với 1.
, ta có thể so sánh chúng với 1.
Suy ra ta có thể so sánh hai phân số 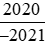 với
với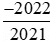 với −1.
với −1.
Cách 1: So sánh hai phân số trên với −1 và áp dunng tính chất bắc cầu.
Ta có: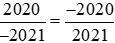
Vì 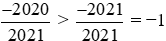
Và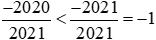
Do đó áp dụng tính chất bắc cầu, ta suy ra: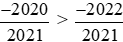 .
.
Vậy 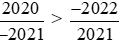 .
.
Cách 2: Đưa hai phân số về cùng mẫu dương rồi so sánh:
Ta có: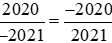 .
.
Vì −2020 > −2022 nên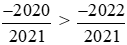 .
.
Vậy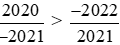 .
.
Bài 4 trang 15 Toán lớp 6 Tập 2: Sắp xếp các số 2;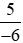 ;
;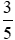 ; −1;
; −1;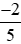 ; 0 theo thứ tự tăng dần.
; 0 theo thứ tự tăng dần.
Lời giải:
Để sắp xếp các phân số theo thứ tự tăng dần hoặc giảm dần, ta làm như sau:
Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.
+ Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.
+ Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.
Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).
Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần hoặc giảm dần (phân số âm luôn bé hơn phân số dương).
a) Ta có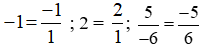 .
.
+ Nhóm các phân số dương: 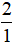 ;
;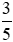 .
.
+ Nhóm các phân số âm: 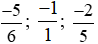
Ta so sánh các phân số trong cùng nhóm với nhau:
+ + Nhóm các phân số dương: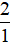 và
và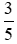
Mẫu số chung: 5.
Ta thực hiện: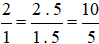 và giữ nguyên phân số
và giữ nguyên phân số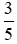 .
.
Vì 5 > 10 nên 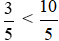 hay
hay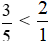 .
.
+ So sánh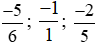 .
.
Mẫu số chung: 30.
Ta thực hiện: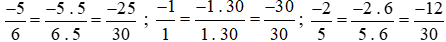
Vì −30 < −25 < −12 nên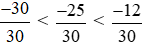 hay
hay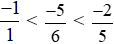 .
.
Từ đó, suy ra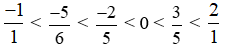
Vậy ta sắp xếp được theo thứ tự tăng dần như sau: −1;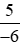 ;
;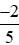 ; 0;
; 0;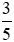 ; 2.
; 2.
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải bài tập Toán lớp 6 Bài 3: So sánh phân số Chân trời sáng tạo (đầy đủ nhất) file PDF hoàn toàn miễn phí.
- Giải bài tập Toán lớp 6 Bài 2: Tính chất cơ bản của phân số Chân trời sáng tạo
- Giải bài tập Toán lớp 6 Bài 2: Hình có tâm đối xứng Chân trời sáng tạo
- Giải bài tập Toán lớp 6 Bài 2: Ba điểm thẳng hàng. Ba điểm không thẳng Chân trời sáng tạo
- Giải bài tập Toán lớp 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia Chân trời sáng tạo
- Giải bài tập Toán lớp 6 Bài 7: Hỗn số Chân trời sáng tạo
- Giải bài tập Toán lớp 6 Bài 5: Phép nhân và phép chia phân số Chân trời sáng tạo
- Giải bài tập Toán lớp 6 Bài 1: Hình có trục đối xứng Chân trời sáng tạo
- Giải bài tập Toán lớp 6 Bài tập cuối chương 9 Chân trời sáng tạo