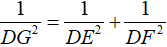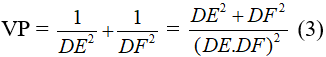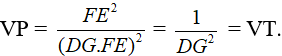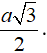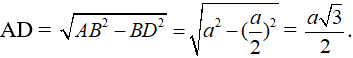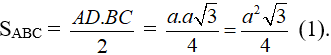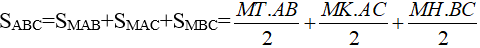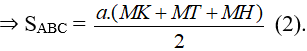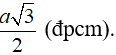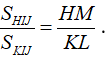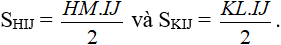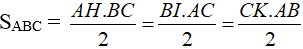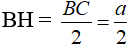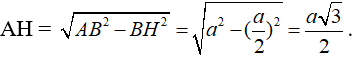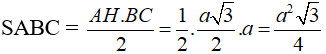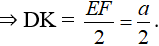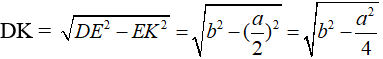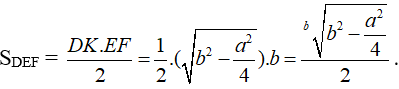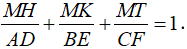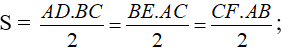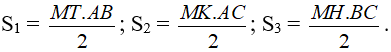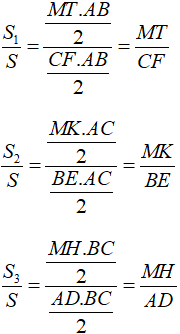Giải Toán lớp 8 VNEN Bài 2: Diện tích hình tam giác

Hướng dẫn giải bài tập Toán lớp 8 VNEN Bài 2: Diện tích hình tam giác chi tiết, dễ hiểu được biên soạn bởi đội ngũ chuyên gia giàu kinh nghiệm chia sẻ. Hy vọng đây sẽ là tài liệu hữu ích hỗ trợ học sinh trong quá trình học tập. Mời các em tham khảo tại đây.

Giải Toán 8 VNEN Bài 2: Hoạt động khởi động

(Trang 122 Toán 8 VNEN Tập 1) Một bạn hỏi, một bạn trả lời, sau đó đổi vai cho nhau:

a) Một đường chéo của hình chữ nhật chia nó thành hai tam giác như thế nào?

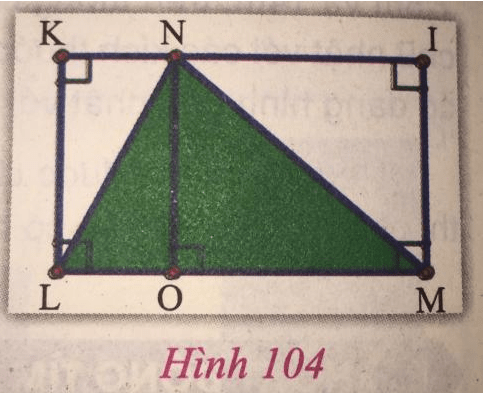
b) Quan sát hình 104, so sánh diện tích hình chữ nhật KNOL với diện tích tam giác vuông NOL.

c) Quan sát hình 104, so sánh diện tích hình chữ nhật KIML với diện tích tam giác vuông NLM.

Lời giải:

a) Một đường chéo của hình chữ nhật chia nó thành hai tam giác bằng nhau.

b) Từ hình 104, dễ dàng nhận thấy diện tích hình chữ nhật KNOL bằng hai lần diện tích tam giác vuông NOL.

c) Từ hình 104, dễ dàng nhận thấy diện tích hình chữ nhật KIML bằng hai lần diện tích tam giác vuông NLM.

Giải Toán VNEN lớp 8 Bài 2: Hoạt động hình thành kiến thức

Câu 1 (Trang 122 Toán 8 VNEN Tập 1)

Luyện tập

- Nếu tam giác vuông có hai cạnh góc vuông là 4cm và 3cm thì diện tích của nó bằng bao nhiêu cm².

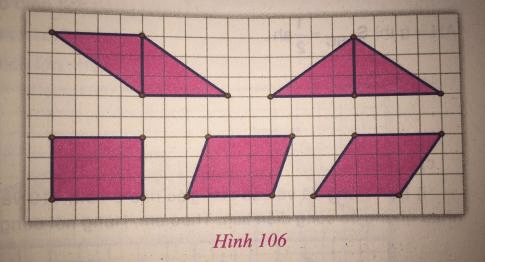
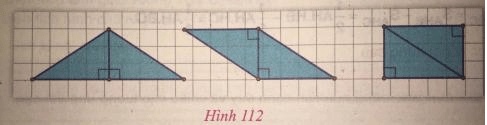
- Trên cùng lưới ô vuông, một bạn đã vẽ các hình như ở hình 106 và cho rằng chúng có cùng diện tích. Theo em, bạn đó nói đúng hay sai? Vì sao?

Lời giải:

- Nếu tam giác vuông có hai cạnh góc vuông là 4cm và 3cm thì diện tích của nó bằng 6cm².

- Bạn đó nói đúng bởi nếu cắt ghép lại các hình tam giác và hình bình hành, ta đều được một hình chữ nhật có chiều dài bằng 4 đơn vị và chiều rộng bằng 3 đơn vị.

Câu 2 (Trang 124 Toán 8 VNEN Tập 1)

Luyện tập

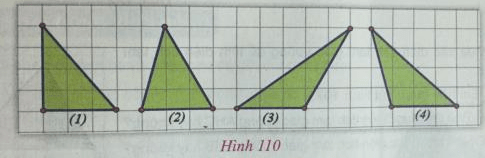
i) Bạn Hùng đã vẽ các tam giác như ở hình 110 và cho rằng chúng không bằng nhau như có chung diện tích. Theo em, bạn Hùng nói vậy là đúng hay sai? Vì sao?

Lời giải:

Dễ dàng nhận thấy các tam giác ở hình 110 không bằng nhau nhưng vì có chung chiều cao và cạnh đáy nên có diện tích bằng nhau.

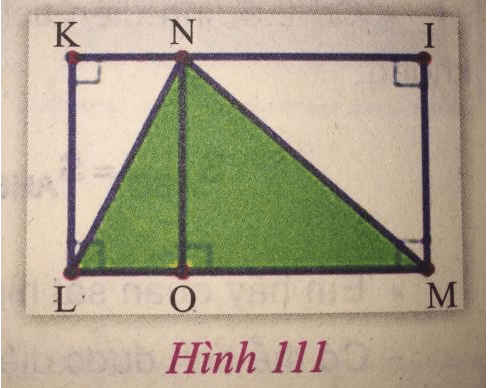
ii) Hãy quan sát hình 111, giải thích tại sao diện tích tam giác NLM bằng nửa diện tích hình chữ nhật IKLM? Có thể dựa vào đó nêu cách tính diện tích tam giác hay không?

Lời giải:

Ta có:

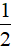
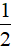
S_NLM = NO.ML = KL.ML (Vì NO = KL)

S_IKLM = KL.ML

Như vậy diện tích tam giác NLM bằng nửa diện tích hình chữ nhật IKLM.

Giải SGK Toán 8 VNEN Bài 2: Hoạt động luyện tập

Câu 1 (Trang 124 Toán 8 VNEN Tập 1)

a) Em hãy cắt tờ giấy mỏng để có hai hình tam giác vuông bằng nhau. Sau đó, hãy ghép hai tam giác đó để tạo thành: một hình bình hành, một hình chữ nhật, một tam giác vuông.

b) Diện tích của mỗi hình trên có bằng nhau không? Vì sao?

Lời giải:

a)

b) Các hình trên bằng nhau vì chúng đều được ghép từ hai hình tam giác vuông bằng nhau.

Câu 2 (Trang 125 Toán 8 VNEN Tập 1)

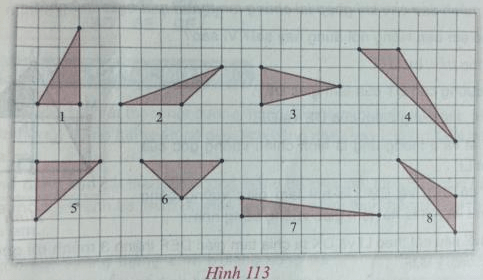
Quan sát hình 113. Nếu chọn mỗi ô vuông là một đơn vị diện tích thì:

a) Những tam giác nào có diện tích bằng nhau?

b) Tam giác nào có diện tích nhỏ nhất?

c) Tam giác nào có diện tích lớn nhất?

Lời giải:

S₁ = 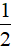.4.2 = 4 (đơn vị diện tích)

S₂ = 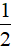.3.2 = 3 (đơn vị diện tích)

S₃ = 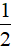.4.2 = 4 (đơn vị diện tích)

S4 = 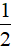.5.2 = 5 (đơn vị diện tích)

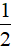
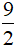
S5 = .3.3 =  (đơn vị diện tích)

S6 = 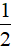.4.2 = 4 (đơn vị diện tích)

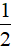
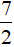
S7 = .7.1 =  (đơn vị diện tích)

S8 = 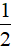.3.2 = 3 (đơn vị diện tích)

a) Tam giác 1, 3, 6 có diện bằng nhau (bằng 4 đơn vị diện tích); tam giác 2 và 8 có diện tích bằng nhau (bằng 3 đơn vị diện tích).

b) Tam giác 2 và 8 có diện tích nhỏ nhất.

c) Tam giác 4 có diện tích lớn nhất.

Câu 3 (Trang 125 Toán 8 VNEN Tập 1)

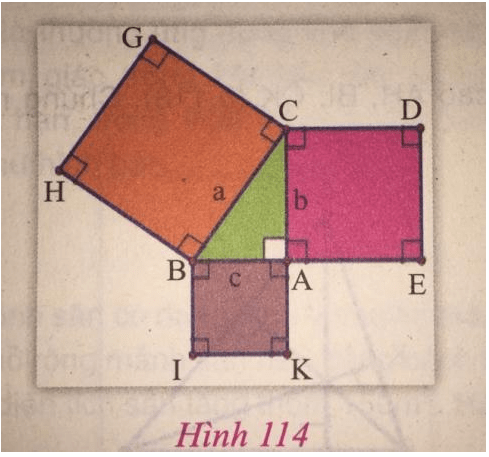
Cho tam giác ABC vuông tại A. Lấy AB, BC, CA làm cạch dựng các hình vuông ACDE, BCGH, ABIK (hình 114).

Lời giải:

Ta có: S_BCGH = BC²;

S_ACDE = AC²;

S_ABIK = AB².

Vì tam giác ABC vuông tại A nên theo định lí Pi-ta-go, ta có: BC² = AC² + AB²

⇒ S_BCGH = S_ACDE + S_ABIK (đpcm).

Câu 4 (Trang 125 Toán 8 VNEN Tập 1)

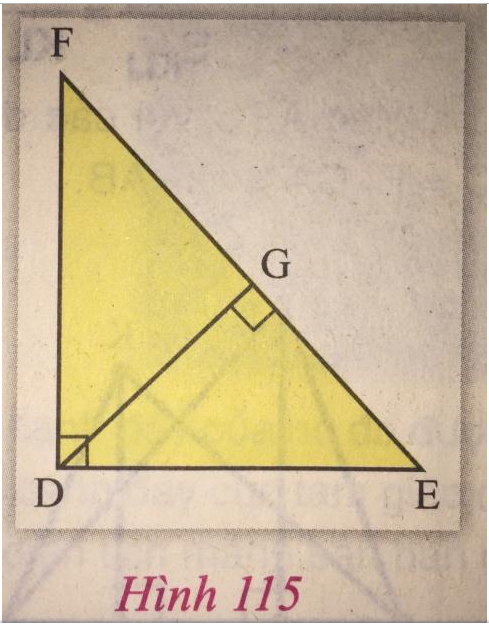
Cho tam giác FDE vuông tại D, có đường cao DG (hình 115).

a) Chứng minh rằng: DE.DF = DG.FE;

b) Chứng minh rằng: 

⇒ DE.DF = DG.FE (đpcm). (1)

b) Vì tam giác DEF vuông tại D nên theo định lí Pi-ta-go, ta có: FE² = DF² + DE² (2)

Có: 

Thay (1), (2) vào (3), ta được: 

Câu 5 (Trang 125 Toán 8 VNEN Tập 1)

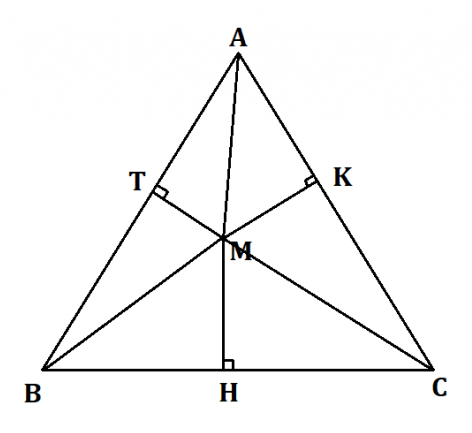
Cho tam giác đều ABC cạnh a và điểm M bất kì nằm trong tam giác đó. Gọi H, K, T tương ứng là hình chiếu vuông góc của điểm M trên BC, CA, AB.

Chứng minh rằng: MH + MK + MT = 

Lời giải:

Từ A kẻ đường thẳng AD. Vì ABC là tam giác đều nên AD đồng thời là đường trung tuyến của tam giác ABC ⇒ BD = .

Theo định lí Pi-ta-go, ta có: 

Khi đó: 

Mặt khác, ta có: 

Từ (1) và (2) ⇒ 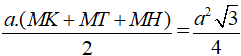 hay MH + MK + MT = 

Giải VNEN Toán 8 Bài 2: Hoạt động vận dụng

Câu 2 (Trang 126 Toán 8 VNEN Tập 1)

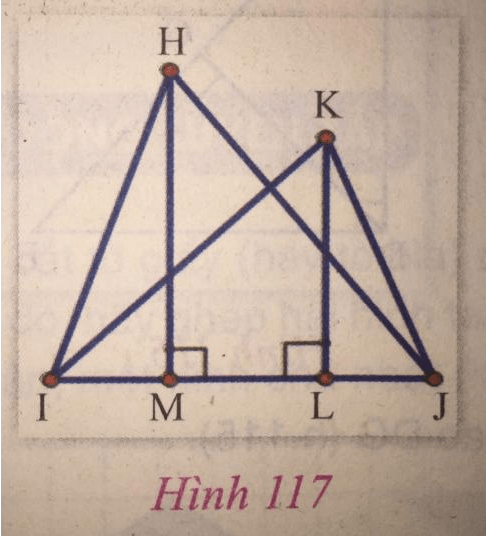
a) Cho tam giác HIJ có đường cao HM, tam giác KIJ có đường cao KL (hình 117). Chứng minh rằng: 

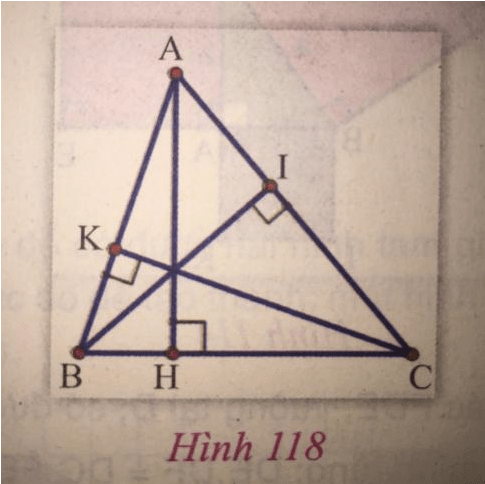
b) Cho tam giác ABC với các đường cao AH, BI, CK (hình 118). Chứng minh rằng: AH.BC = BI.CA = CK.AB.

Lời giải:

a) Ta có: 

Như vậy: 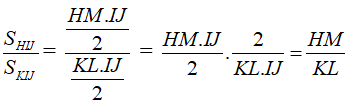 (đpcm).

b) Vì AH, BI, CK đều là đường cao của tam giác ABC nên ta có:

⇒ AH.BC = BI.CA = CK.AB (đpcm).

Câu 3 (Trang 126 Toán 8 VNEN Tập 1)

a) Cho tam giác đều cạnh a. Hãy tính diện tích tam giác này theo a.

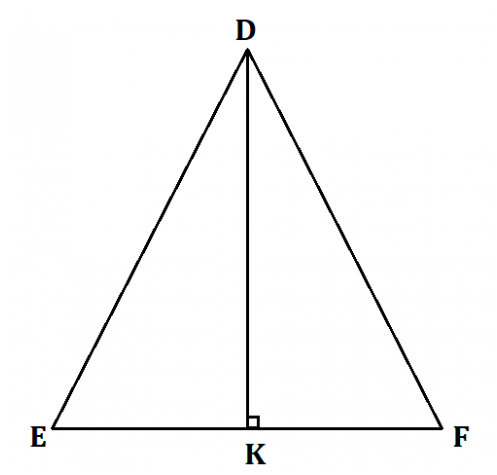
b) Cho tam giác cân có cạnh đáy là a, cạnh bên là b. Hãy tính diện tích tam giác này theo a và b.

Lời giải:

a)

Xét tam giác ABC đều có cạnh bằng a, đường cao AH.

Vì tam giác ABC đều nên đường cao AH đồng thời là đường trung tuyến ⇒ 

Áp dụng định lí Pi-ta-go vào tam giác AHB vuông tại H, ta có:

Như vậy: 

b)

Xét tam giác DEF cân tại D có cạnh đáy bằng a, cạnh bên bằng b, đường cao DK.

Vì tam giác DEF cân tại D nên đường cao DK đồng thời là đường trung tuyến

Áp dụng định lí Pi-ta-go vào tam giác DKE vuông tại K, ta có:

Như vậy: 

Câu 4 (Trang 126 Toán 8 VNEN Tập 1)

Một mảnh ruộng có dạng một tam giác vuông. Biết rằng tổng độ dài hai cạnh góc vuông của nó là 350m và độ dài cạnh góc vuông thứ nhất gấp 4 lần cạnh góc vuông thứ 2. Diện tích mảnh ruộng trên bằng bao nhiêu m²?

Lời giải:

Gọi x là độ dài cạnh góc vuông thứ hai.

⇒ Độ dài cạnh góc vuông thứ nhất là 4x.

Theo đề bài, ta có phương trình:

4x + x = 350 ⇒ 5x = 350 ⇒ x = 70

⇒ Độ dài cạnh góc vuông thứ nhất là 4.70 = 280.

Như vậy diện tích của mảnh ruộng là: 280.70 = 19600(m²).

Câu 5 (Trang 127 Toán 8 VNEN Tập 1)

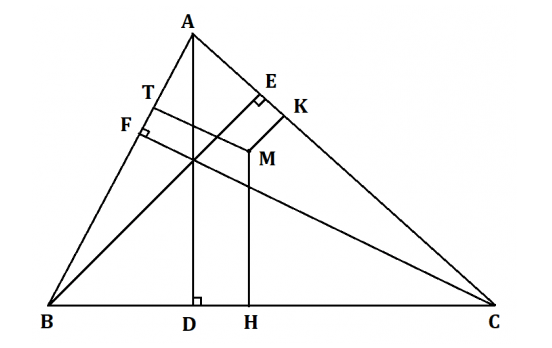
Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE, CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K.Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T. Chứng minh rằng

Lời giải:

Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S₁, S₂, S₃.

Ta có: S = S₁ + S₂ + S₃.

Trong đó: 

Lại có:

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán lớp 8 VNEN Tập 1 Bài 2: Diện tích hình tam giác file PDF hoàn toàn miễn phí.