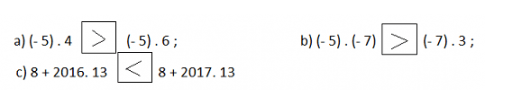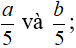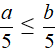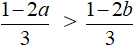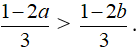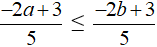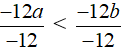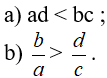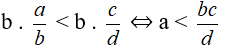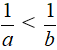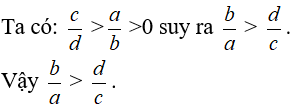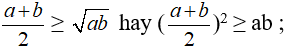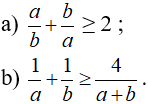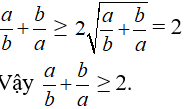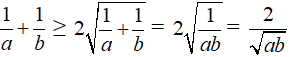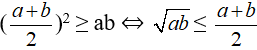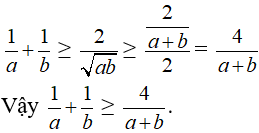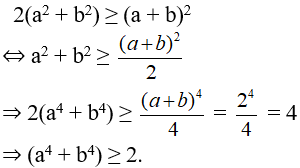Giải Toán lớp 8 VNEN Bài 3: Luyện tập chung

Hướng dẫn giải bài tập Toán lớp 8 VNEN Bài 3: Luyện tập chung chi tiết, dễ hiểu được biên soạn bởi đội ngũ chuyên gia giàu kinh nghiệm chia sẻ. Hy vọng đây sẽ là tài liệu hữu ích hỗ trợ học sinh trong quá trình học tập. Mời các em tham khảo tại đây.

Giải Toán 8 VNEN Bài 3: Hoạt động luyện tập

Câu 1 (Trang 32 Toán 8 VNEN Tập 2)

Điền dấu thích hợp (<, >, ≤, ≥) vào ô vuông:

Lời giải:

Ta có:

Câu 2 (Trang 32 Toán 8 VNEN Tập 2)

a) So sánh (- 2) . 3 và - 4,5.

b) Từ kết quả câu

a) hãy suy ra các bất đẳng thức sau:

(- 2) . 30 < - 45 ;            (- 2) . 3 + 4,5 < 0

Lời giải:

a) So sánh: (- 2) . 3 < - 4,5.

b) * Ta có: (- 2) . 3 < - 4,5

Nhân cả hai vế của bất đẳng thức trên với 10 ta được:

(- 2) . 3 . 10 < - 4,5 . 10 ⇔ (- 2) . 30 < - 45

* Ta có: (- 2) . 3 < - 4,5

Cộng cả hai vế của bất đẳng thức trên với 4,5 ta được:

(- 2) . 3 + 4,5 < - 4,5 + 4,5 ⇔ (- 2) . 3 + 4,5 < 0

Câu 3 (Trang 32 Toán 8 VNEN Tập 2)

Cho a ≤ b, hãy so sánh:

a) - 9a và - 9b ;

b) 

c) a + 1 và b + 2 ;

d) 2a - 1 và 2b + 1.

Lời giải:

a) Ta có: a ≤ b

Nhân cả hai vế của bất đẳng thức trên với (- 9) ta được:

- 9a ≥ - 9b

b) Ta có: a ≤ b

Chia cả hai vế của bất đẳng thức trên với 5 ta được:

c) Ta có: a ≤ b

Cộng cả hai vế của bất đẳng thức trên với 1 ta được:

a + 1 ≤ b + 1 < b + 2

Vậy a + 1 < b + 2

d) Ta có: a ≤ b (1)

Nhân cả hai vế của bất đẳng thức (1) với 2 ta được:

2a ≤ 2b (2)

Cộng cả hai vế của bất đẳng thức (2) với (- 1) ta được:

2a - 1 ≤ 2b - 1 < 2b + 1

Vậy 2a - 1 < 2b + 1.

Câu 4 (Trang 33 Toán 8 VNEN Tập 2)

Cho a < b, chứng tỏ rằng:

a) 3 - 6a > 1 - 6b ;

b) 7(a - 2) < 7(b - 2) ;

c) 

Lời giải:

a) Ta có: a < b

Nhân cả hai vế của bất phương trình trên với (- 6) ta được:

- 6a > - 6b

Cộng cả hai vế của bất phương trình trên với 1 ta được:

1 - 6a > 1 - 6b

Mặt khác 3 - 6a > 1 - 6a suy ra 3 - 6a > 1 - 6b.

b) Ta có: a < b

Nhân cả hai vế của bất phương trình trên với 7 ta được:

7a < 7b

Cộng cả hai vế của bất phương trình trên với (- 14) ta được:

7a - 14 < 7b - 14 ⇔ 7(a - 2) < 7(b - 2).

c) Ta có: a < b

Nhân cả hai vế của bất phương trình trên với (- 2) ta được:

- 2a > - 2b

Cộng cả hai vế của bất phương trình trên với 1 ta được:

1 - 2a > 1 - 2b

Chia cả hai vế của bất phương trình trên với 3 ta được:

Câu 5 (Trang 33 Toán 8 VNEN Tập 2)

So sánh a và b nếu:

a) a + 23 < b + 23 ;

b) - 12a > - 12b

c) 5a - 6 ≥ 5b - 6 ;

d) 

Lời giải:

a) Ta có: a + 23 < b + 23

Cộng cả hai vế của bất phương trình trên với (- 23) ta được:

a + 23 + (- 23) < b + 23 + (- 23) ⇔ a < b.

b) Ta có: - 12a > - 12b

Chia cả hai vế của bất phương trình trên với (- 12) ta được:

⇔ a < b

c) 5a - 6 ≥ 5b - 6

Cộng cả hai vế của bất phương trình trên với 6 ta được:

5a - 6 + 6 ≥ 5b - 6 + 6 ⇔ 5a ≥ 5b

Chia cả hai vế của bất phương trình trên với 5 ta được:

a ≥ b

d) Ta có: 

Nhân cả hai vế của bất phương trình trên với 5 ta được:

- 2a + 3 ≤ -2b + 3

Cộng cả hai vế của bất phương trình trên với ( - 3) ta được:

- 2a ≤ - 2b

Chia cả hai vế của bất phương trình trên với ( -2) ta được:

a ≥ b

Giải Toán VNEN lớp 8 Bài 3: Hoạt động vận dụng

Câu 1 (Trang 33 Toán 8 VNEN Tập 2)

Cho bốn số dương a, b, c, d thỏa mãn 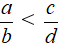 Chứng minh rằng:

Lời giải:

a) Ta có:

 Nhân hai vế của bất phương trình trên với b (b > 0) ta được:

Vậy ad < bc.

b)

Ta có tính chất: nếu a > b > 0 thì 

Câu 2 (Trang 33 Toán 8 VNEN Tập 2)

Chứng minh rằng với mọi số a ta luôn có:

a) a² + a + 1 ≥ 0 ;

b) – a² - 6a ≤ 9

Lời giải:

a) Ta có: a² + a + 1 = a² + 2.a.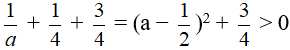 với mọi a

Vậy a² + a + 1 > 0

b) Xét hiệu: (- a² - 6

a) - 9 = - (a² + 6a + 9) = - (a+3)² ≤ 0 với mọi a

Vậy – a² - 6a - 9 ≤ 0 hay – a² - 6a ≤ 9

Câu 3 (Trang 33 Toán 8 VNEN Tập 2)

Chứng minh rằng với mọi số a, b, c ta luôn có:

a) a² + b² ≥ 2ab ;

b) a² + b² + c² ≥ ab + bc + ca.

Lời giải:

a) Xét hiệu: (a² + b²) - 2ab = (a−b)² ≥ 0 với mọi a, b

Vậy a² + b² ≥ 2ab với mọi a, b.

b) Ta có:

a² + b² ≥ 2ab

b² + c² ≥ 2bc

c² + a² ≥ 2ca

Cộng 3 bất phương trình theo vế ta được:

2(a² + b² + c²) ≥ 2(ab + bc + ca)

⇔ a² + b² + c² ≥ ab + bc + ca

Vậy a² + b² + c² ≥ ab + bc + ca. với mọi a, b, c

Giải SGK Toán 8 VNEN Bài 3: Hoạt động tìm tòi mở rộng

Câu 1 (Trang 33 Toán 8 VNEN Tập 2)

Bất đẳng thức Cô-si

Bất đẳng thức Cô-si cho hai số không âm a và b:

( Trung bình cộng của hai số không âm lớn hơn hoặc bằng trung bình nhân của chúng).

Đẳng thức xảy ra khi a = b.

Bất đẳng thức này mang tên nhà toán học người Pháp Cô-si (Augustin Louis Cauchy, 1789 - 1857).

Áp dụng bất đẳng thức Cô-si, chứng minh các bất đẳng thức sau với a,b là hai số dương:

Lời giải:

a) Theo bất đẳng thức Cô-si:

 (a, b là số dương), ta có:

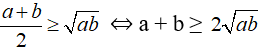
b) Theo bất đẳng thức Cô-si ta có:

Mặt khác ta có theo bất đẳng thức Cô-si: 

Suy ra:

Câu 2 (Trang 34 Toán 8 VNEN Tập 2)

2. Bất đẳng thức Bu-nhi-a-cốp-xki

Bất đẳng thức Bu-nhi-a-cốp-xki cho hai cặp số (a; b) và (x; y):

(ax+by)² ≤ (a² + b²)(x² + y²);

Đẳng thức này xảy ra khi và chỉ khi ay = bx, hay 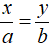(khi ab ≠ 0).

Bất đẳng thức này mang tên nhà toán học người Nga Bu-nhi-a-cốp-xki (Viktor Bunyakovsky, 1804 - 1889).

Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki, chứng minh các bất đẳng thức sau:

a) 2(a² + b²) ≥ (a + b)² ;

b) a⁴ + b⁴ ≥ 2, biết rằng a + b = 2.

Lời giải:

a) Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki cho cặp số (1 ; 1) và (a; b)ta có:

(12 + 12)(a² + b²) ≥ (1.a+1.

b)² = (a + b)²

Dấu bằng xảy ra khi a = b.

Vậy 2(a² + b²) ≥ (a + b)²

b) Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki cho cặp số (1; 1) và (a²; b²) ta có:

(12 + 12)(a⁴ + b⁴) ≥ (1.a²+1.b²)² = (a²+b²)²

Theo câu a:

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán lớp 8 VNEN Tập 2 Bài 3: Luyện tập chung file PDF hoàn toàn miễn phí.