Giải SBT Tin học 7 Bài 12: Vẽ hình phẳng bằng GEOGEBRA (Quyển 2) đầy đủ nhất
Mời các em học sinh và quý thầy cô tham khảo ngay hướng dẫn giải sách bài tập Tin học lớp 7 Bài 12:Vẽ hình phẳng bằng GEOGEBRA (Quyển 2) đầy đủ và rõ ràng dưới đây.
Bài 1 (trang 71 SBT Tin học 7 Bài 12)
Các đối tượng a ,b, c được khởi tạo trong cửa sổ CSA của GeoGebra như sau:
a:=1 b:= a^2 c:=(a+b)^3
Trong ba đối tượng trên đối tượng nào là tự do?
(A) a ,b, c đều là tự do;
(B) a,b là tự do; c phụ thuộc;
(C) a là tự do; b,c là phụ thuộc;
(D) a ,b ,c đều là phụ thuộc.
Lời giải:
Đáp án: C
Bài 2 (trang 71 SBT Tin học 7 Bài 12)
Trong GeoGebra các đối tượng nào dưới đây có thể là tự do?
1.Số; 2. Hàm số; 3. Điểm; 4. Đoạn thẳng;
(A) Tất cả các đối tượng trên đều có thể tự do;
(B) Chỉ có Số và Điểm mới có thể tự do;
(C) Chỉ có Số, Điểm và Hàm số mới có thể tự do;
(D) Chỉ có Số mới có thể tự do.
Đáp án: C
Bài 3 (trang 72 SBT Tin học 7 Bài 12)
Mệnh đề nào sau đây đúng?
(A) GeoGebra là phần mềm dùng để giải các bài toán hình học và đại số;
(B) GeoGebra là phần mềm hỗ trợ giúp giáo viên và học sinh giải các bài tập toán;
(C) GeoGebra là phần mềm có chức năng vẽ hình và giải toán;
(D) GeoGebra là phần mềm có chức năng vẽ hình chính xác để hỗ trợ việc dạy và học của giáo viên và học sinh.
Đáp án: D
Bài 4 (trang 72 SBT Tin học 7 Bài 12)
Thế nào là một đối tượng hình học?
(A) Là một hình tròn vẽ trên màn hình;
(B) Là một điểm vẽ trên màn hình;
(C) Là một đoạn thẳng vẽ trên màn hình;
(D) Là một phần cơ bản của hình như điểm, đoạn , đường, tia, đường tròn.
Đáp án: D
Bài 5 (trang 72 SBT Tin học 7 Bài 12)
Nếu trên mặt phẳng chúng ta nhìn thấy một đường thẳng và một điểm nằm trên đường thẳng này thì hai đối tượng điểm và đường thẳng quan hệ với nhau như thế nào?
(A) Hai đối tượng trên không có quan hệ gì với nhau;
(B) Chưa thể nói gì về quan hệ giữa hai đối tượng này;
(C) Hai đối tượng điểm và đường thẳng cùng phụ thuộc vào nhau;
(D) Chỉ có thể xảy ra một trong hai trường hợp, hoặc đối tượng điểm phụ thuộc vào đường thẳng hoặc đối tượng đường thẳng phụ thuộc vào điểm.
Đáp án: B
Bài 6 (trang 72 SBT Tin học 7 Bài 12)
Vì sao các hình được vẽ bằng phần mềm GeoGebra được gọi là hình học động?
(A) Vì các hình này tự động chuyển động được;
(B) Vì các hình này không đứng yên tại một chỗ;
(C) Vì người dùng có thể di chuyển các hình này trên màn hình;
(D) Vì người dùng có thể di chuyển các hình này trên màn hình mà vẫn giữ nguyên được quan hệ hình học giữa các đối tượng của hình.
Đáp án: D
Bài 7 (trang 72 SBT Tin học 7 Bài 12)
Nếu điểm A luôn nằm trên đường thẳng d thì quan hệ giữa điểm A và đường thẳng d như thế nào ?
(A) Các đối tượng A và d không có quan hệ với nhau;
(B) Đối tượng A có quan hệ phụ thuộc vào d;
(C) Đối tượng d có quan hệ hụ thuộc vào A ;
(D) Hai đối tượng A, d có quan hệ phụ thuộc lẫn nhau.
Đáp án: B
Bài 8 (trang 73 SBT Tin học 7 Bài 12)
Cho trước điểm A, đường thẳng d đi qua A. Quan hệ giữa điểm A và đường thẳng d như thế nào ?
(A) Các đối tượng A và d không có quan hệ với nhau;
(B) Đối tượng A có quan hệ phụ thuộc vào d;
(C) Đối tượng d có quan hệ hụ thuộc vào A ;
(D) Hai đối tượng A, d có quan hệ phụ thuộc lẫn nhau.
Đáp án: C
Bài 9 (trang 73 SBT Tin học 7 Bài 12)
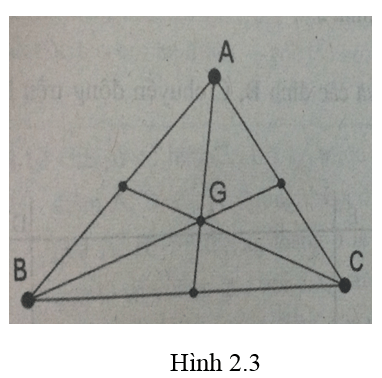
Vẽ tam giác ABC với ba trung tuyến và trọng tâm G(hình 2.3)
Lời giải:
- Dùng công cụ Đoạn thẳng 
lần lượt vẽ các cạnh AB, BC, CA. Lưu ý các điểm A, B, C có thể chọn bất kì
- Dùng công cụ Trung điểm và tâm 
xác định ba trung điểm của của các cạnh AB, BC, CA bằng cách chọn công cụ, nháy chuột lên một đoạn thẳng để tạo trung điểm
- Dùng công cụ Đoạn thẳng nối cách đỉnh A, B, C với trung điểm các cạnh đối diện
- Dùng công cụ Điểm để xác định giao điểm của ba đường trung tuyến, đổi tên điểm này là G
Bài 10 (trang 73 SBT Tin học 7 Bài 12)
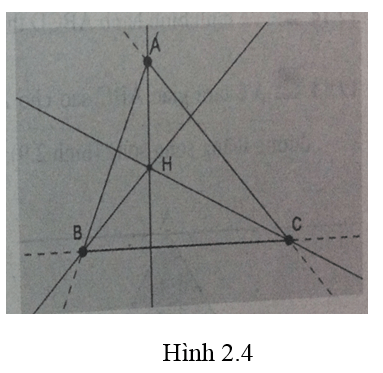
Vẽ tam giác ABC với ba đường cao và trực tâm H ( hình 2.4)
Lời giải:
- Dùng công cụ Điểm 
xác định ba điểm A, B, C bất kì.
- Dùng công cụ Đường thẳng 
nối các đường AB, BC, CA. Sau đó có thể thay đổi các đường này thành đường nét đứt
- Dùng công cụ Đường vuông góc 
lần lượt kẻ các đường thẳng hạ từ A, B, C xuống các cạnh đối diện
- Dùng công cụ Điểm để xác định giao điểm của ba đường cao, đổi tên điểm này là H
- Dùng công cụ Đoạn thẳng 
lần lượt nối các cạnh AB, BC, CA tạo hình ảnh tam giác với các đường vẽ liền
Bài 11 (trang 73 SBT Tin học 7 Bài 12)
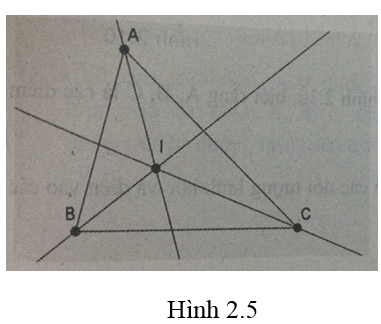
Vẽ tam giác ABC với ba phân giác giao nhau tại một điểm I ( hình 2.5)
Lời giải:
- Dùng công cụ Đoạn thẳng 
lần lượt vẽ các cạnh AB, BC, CA. Lưu ý các điểm A, B, C có thể chọn bất kì
- Dùng công cụ Đường phân giác 
lần lượt vẽ ba đường phân giác các góc A, B, C
- Dùng công cụ Điểm 
để xác định giao điểm của ba đường phân giác, đổi tên điểm này là I
Bài 12 (trang 74 SBT Tin học 7 Bài 12)
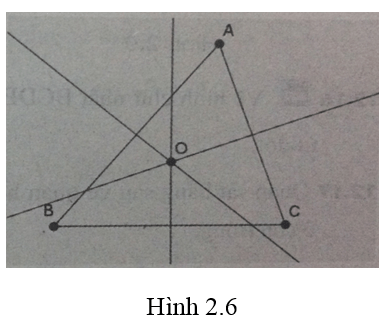
Vẽ tam giác ABC với ba đường trung trực của các cạnh giao nhau tại điểm O ( Hình 2.6)
Lời giải:
- Dùng công cụ Đoạn thẳng 
lần lượt vẽ các cạnh AB, BC, CA. Lưu ý các điểm A, B, C có thể chọn bất kì
- Dùng công cụ Đường trung trực 
lần lượt vẽ ba đường trung trực của các cạnh AB, BC, CA
- Dùng công cụ Điểm 
để xác định giao điểm của ba đường trung trực, đổi tên điểm này là O
Bài 13 (trang 74 SBT Tin học 7 Bài 12)
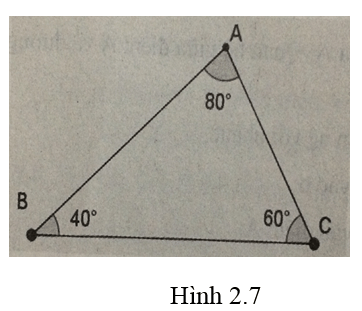
Vẽ tam giác với số đo các góc như hình 2.7.
Lời giải:
- Dùng công cụ Đoạn thẳng 
lần lượt vẽ các cạnh AB, BC, CA. Lưu ý các điểm A, B, C có thể chọn bất kì
- Dùng công cụ Góc 
để tạo ra các góc A, B, có số đo góc hiện trên màn hình. Lưu ý cần thiết lập chế độ làm tròn số với 0 chữ số thập phân trước đó
- Chuyển sang chế độ chọn (nhấn phím ESC hoặc chọn công cụ)
- Kéo thả điểm Asao cho góc B trở thành 40o
- Kéo thả điểm C sao cho góc A trở thành 80o
Bài 14 (trang 74 SBT Tin học 7 Bài 12)
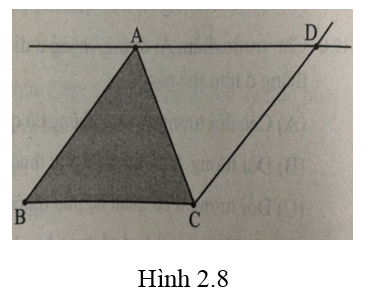
Vẽ hình bình hành ABCD theo hình 2.8.
Lời giải:
- Dùng công cụ Đa giác 
để vẽ tam giác ABC bằng cách chọn lần lượt các điểm A, B, C. Cuối cùng, nháy chuột vào điểm A để kết thúc vẽ
- Dùng công cụ Đường song song 
lần lượt vẽ qua A đường thẳng song song với BC, vẽ qua C đường thẳng song song với AB
- Dùng công cụ Điểm 
để xác định giao điểm của hai đường thẳng song song vừa tạo ra,. Đổi tển điểm này là D
- Dùng công cụ Đoạn thẳng 
để nối các cạnh của hình bình hành
Bài 15 (trang 74 SBT Tin học 7 Bài 12)
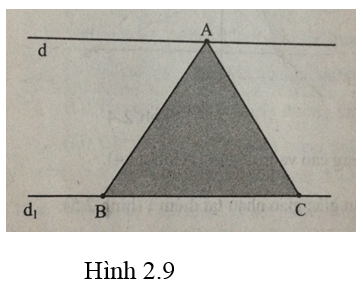
Vẽ tam giác ABC sao cho A và các đỉnh B, C chuyển động trên hai đường thẳng song song( hình 2.9).
Lời giải:
- Dùng công cụ Đường thẳng 
vẽ đường thẳng d
- Dùng công cụ Điểm 
vẽ một điểm bất kì nằm ngoài đường thẳng d. Giả sử điểm này là M
- Dùng công cụ Đường song song 
, vẽ đường thẳng d1 đi qua điểm M và song song với d
Bài 16 (trang 74 SBT Tin học 7 Bài 12)
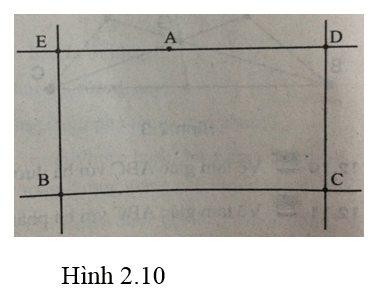
Vẽ hình chữ nhật BCDE như hình 2.10, biết rằng A, B, C là các điểm tự do.
Lời giải:
- Dùng công cụ Điểm 
vẽ ba điểm A, B, C bất kì
- Dùng công cụ Đường thẳng 
nối hai điểm B, C
- Dùng công cụ Đường song song 
, vẽ đường thẳng đi qua A và song song với BC
- Dùng công cụ Đường vuông góc 
lần lượt kẻ từ các điểm B, C hai đường vuông góc với BC
- Làm ẩn điểm M
- Dùng công cụ Điểm tạo hai điểm B, C trên đường thẳng d1 và tạo điểm A trên đường thẳng d
- Dùng công cụ Đa giác 
nối các điểm A, B, C để tạo ra tam giác ABC
Bài 17 (trang 74 SBT Tin học 7 Bài 12)
Quan sát bảng sau về quan hệ giữa các đối tượng hình học và điển vào các ô còn trống .
| Hình thực tế | Mô tả quan hệ | Đối tượng bị phụ thuộc( cha) | Đối tượng phụ thuộc ( con) |
| Điểm A,B nằm trên đường thẳng d | nằm trên | d | A,B |
| A là giao điểm của đường thẳng d và | giao điểm | d, d1 | A |
| d là phân giác của góc ABC | phân giác | A, B, C | |
| M là trung điểm cạnh AB | trung điểm | A, B | |
| h là đường cao hạ từ điểm A xuống cạnh BC | vuông góc | ||
| α là góc tạo bởi ba điểm A, B,C | góc tạo bởi ba điểm | α |
Lời giải:
| Hình thực tế | Mô tả quan hệ | Đối tượng bị phụ thuộc( cha) | Đối tượng phụ thuộc ( con) |
| Điểm A,B nằm trên đường thẳng d | nằm trên | d | A,B |
| A là giao điểm của đường thẳng d và | giao điểm | d, d1 | A |
| d là phân giác của góc ABC | phân giác | A, B, C | d |
| M là trung điểm cạnh AB | trung điểm | AB | m |
| h là đường cao hạ từ điểm A xuống cạnh BC | vuông góc | A, BC | h |
| α là góc tạo bởi ba điểm A, B,C | góc tạo bởi ba điểm | A, B, C | α |
Bài 18 (trang 75 SBT Tin học 7 Bài 12)
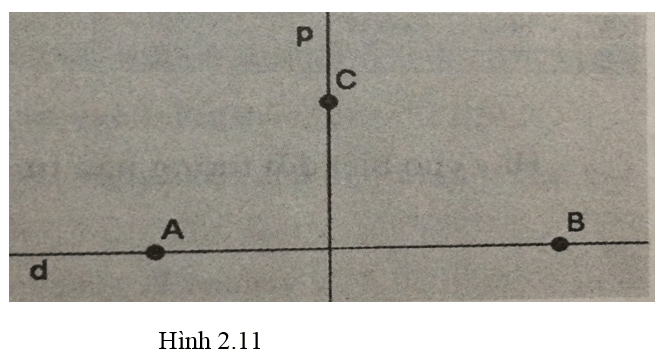
Giả sử có hình 2.11 . Cho trước ba điểm A, B,C . Vẽ đường thẳng d đi qua A,B . Vẽ đường thẳng p là đi qua C và vuông góc với d. Quan hệ giữa đường thẳng p và điểm A là gì ?
(A) Không phụ thuộc vào nhau.
(B) A phụ thuộc vào p.
(C) p phụ thuộc vào A; p là đối tượng con của A;
(D) p phụ thuộc vào điểm A, B,C và đường thẳng d.
Lời giải:
Đáp án: D
Bài 19 (trang 75 SBT Tin học 7 Bài 12)
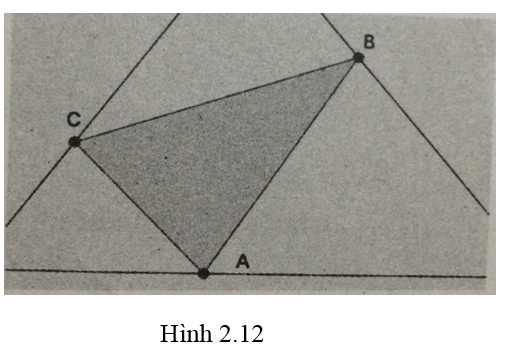
Vẽ tam giác ABC như hình 2.12 trong đó các điểm A , B, C chuyển động trên ba đường thẳng cho trước .
Lời giải:
- Dùng công cụ Đường thẳng 
vẽ ba đường thẳng
- Dùng công cụ Điểm 
để xác định ba điểm A, B, C nằm trên đường thẳng vừa vẽ
- Dùng công cụ Đa giác 
nối các điểm A, B, C để tạo tam giác ABC
Bài 20 (trang 76 SBT Tin học 7 Bài 12)
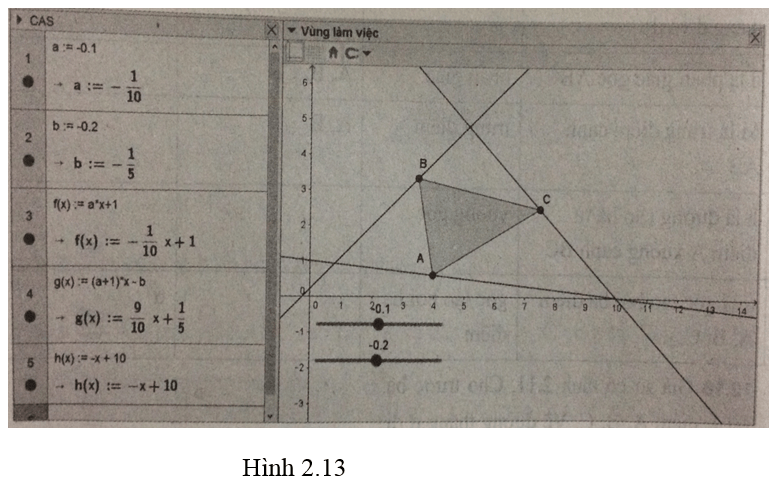
Vẽ hình theo mô tả dưới đây ( hình 2.13)
- Các đối tượng a,b bất kì có đối tượng thanh trượt điều khiển đối tượng này.
- Thiết lập ba hàm số : f(x)= ax+1 ; g(x)= (a+1)x – b; h(x)= -x +10;
- Các điểm A , B , C chuyển động tương ứng trên đồ thị f, g, h.
- Vẽ tam giác ABC. 
Hãy cho biết đối tượng nào tự do, đối tượng nào phụ thuộc?
Lời giải:
Các đối tượng tự do: a, b, h(x);
Các đối tượng phụ thuộc: f(x), g(x), A, B, C, tam giác ABC
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải sách bài tập Tin học lớp 7 Bài 12:Vẽ hình phẳng bằng GEOGEBRA (Quyển 2) file PDF hoàn toàn miễn phí.
- Giải SBT Tin học 7 Bài 1: Chương trình bảng tính là gì? (Quyển 2) đầy đủ nhất
- Giải SBT Tin học 7 Bài 4: Sử dụng các hàm để tính toán (Quyển 2) đầy đủ nhất
- Giải SBT Tin học 7 Bài 5: Thao tác với bảng tính (Quyển 2) đầy đủ nhất
- Giải SBT Tin học 7 Bài 3: Thực hiện tính toán trên trang tính (Quyển 2) đầy đủ nhất
- Giải SBT Tin học 7 Bài 2: Các thành phần chính và dữ liệu trên trang tính (Quyển 2) đầy đủ nhất
- Giải SBT Tin học 7 Bài 7: Trình bày và in trang tính (Quyển 2) đầy đủ nhất
- Giải SBT Tin học 7 Bài 12: Vẽ hình phẳng bằng GEOGEBRA (Quyển 2) đầy đủ nhất
- Giải SBT Tin học 7 Bài 8: Sắp xếp và lọc dữ liệu (Quyển 2) đầy đủ nhất
