20 Câu hỏi trắc nghiệm Toán 12 Bài 3: Lôgarit (có đáp án)

Bộ câu hỏi và bài tập trắc nghiệm Toán 12 Lôgarit được chúng tôi sưu tầm và tổng hợp bao gồm những dạng câu hỏi trọng tâm và thường xuất hiện trong bài kiểm tra quan trọng. Mời các em học sinh và quý thầy cô giáo theo dõi chi tiết dưới đây.

Bộ 20 bài tập trắc nghiệm Toán 12 Lôgarit

Câu 1: Biết 3 + 2log₂x = log₂y . Hãy biểu thị y theo x

A. y = 2x+3   

B. y = 8x²    

C. y = x²+8    

D. y = 3x²

Câu 2: Nếu x = (log₈2)^log₂8 thì log₃x bằng:

A. -3    

B. -1/3   

C. 1/3    

D. 3

Câu 3: Độ pH của một chất được xác định bởi công thức pH = -log[H⁺] trong đó [H⁺] là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H⁺ của một chất biết rằng độ pH của nó là 2,44

A. 1,1.108 mol/L    

B. 3,2.10-4 mol/L    

C. 3,6.10-3 mol/L

D. 3,7.10-3 mol/L

Câu 4: Rút gọn biểu thức

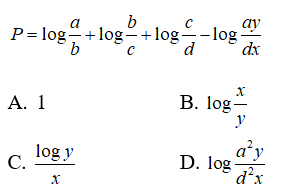
Câu 5: Tính giá trị biểu thức

A. 0,01   

B. 0,1   

C. 1   

D. 10

Câu 6: Đặt a = log₂3, b = log₃5. Hãy tính biểu thức P = log₆60 theo a và b

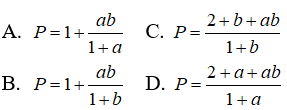
Câu 7:

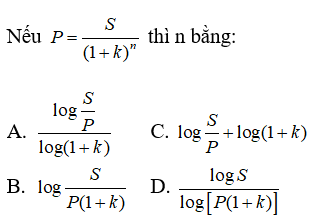
Câu 8: Tính giá trị của biểu thức log₃100 - log₃18 - log₃50

A. -3    

B. -2    

C. 2    

D. 3

Câu 9: Tính giá trị của biểu thức (log₂3)(log₉4)

A. 2/3    

B. 1   

C. 3/2    

D. 4

Câu 10: Tính giá trị của biểu thức

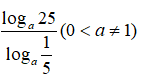
A. -2    

B. 2    

C. -3log_a5    

D. 3log_a5

Câu 11: 10^log7 bằng:

A. 1   

B. log₇10   

C. 7   

D. log7

Câu 12: Cho P = log₃(a²b³) (a,b là các số dương). Khẳng định nào sau đây là đúng ?

A. P = 6lpg₃a.log₃b   

B. P = 2log₃a + 3log₃b

C. P = (1/2)log₃a + (1/3)log₃b    

D. P = (log₃a)².(log₃b)³

Câu 13: Đặt a = log₂7, b = log₂3. Tính log₂(56/9) theo a và b

A. P = 3 + a - 2b    

B. P = 3 + a - b²   

C. P = 3a/2b    

D. 3a/b²

Câu 14: Biết y = 2^3x. Hãy biểu thị x theo y

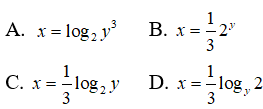
Câu 15: Biết rằng log₃y = (1/2)log₃u + log₃v + 1. Hãy biểu thị y theo u và v

A. y = 3√uv    

B. y = 3u²v    

C. y = 3 + √u + v    

D. y = (√uv)³

Câu 16: Tìm số k sao cho 2^x = e^kx với mọi số thực x

A. k = √2    

B. k = 2^x   

C. k = log₂e    

D. k = ln2

Câu 17: Độ pH của một chất được xác định bởi công thức pH = -log[H⁺] trong đó H⁺ là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H⁺ của một chất biết rằng độ pH của nó là 8,06

A. 8,7.10^-9 mol/L    

B. 2,44.10^-7 mol/L

C. 2,74,4 mol/L    

D. 3,6.10^-7 mol/L

Câu 18: log125 bằng

A. 5log3    

B. 3 - 3log2    

C. 100log1,25    

D. (log25)(log5)

Câu 19: Cho a, b, c là các số dương. Tính giá trị của biểu thức log_ab².log_bc².log_ca²

A. 1/8    

B. 1   

C. 8   

D. 6

Câu 20: Tính giá trị của biểu thức

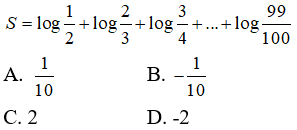
Đáp án và lời giải câu hỏi trắc nghiệm Toán 12 Lôgarit

Câu 1:

3 + 2log₂x = log₂y ⇔ log₂2³ + log₂x² = log₂y

Chọn đáp án B

Câu 2:

x = (log₈2)^log₂8 = (log_2³2)^log₂23 = (1/3)³ = 3^-3 => log₃x = -3

Chọn đáp án A

Câu 3:

pH = -log[H⁺]

=> [H⁺] = 10^-pH = 10^-2,44 ≈ 0,00363 ≈ 3,6.10^-3 (mol/L).

Chọn đáp án C

Câu 4:

Ta có

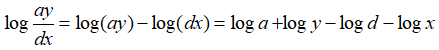
P = loga - logb + logb - logc + logc - logd - (loga + logy - logd - logx)

= -logy + logx = log(x/y)

Chọn đáp án B

Câu 5;

Biểu thức đã cho bằng

log_100!2 + log_100!3 + log_100!4 + ... + log_100!100 = log_100!(2.3.4....10) = log_100!100! = 1

Chọn đáp án C

Câu 6:

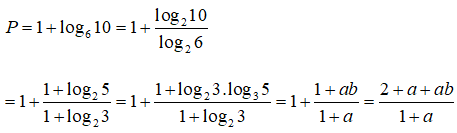
Chọn đáp án D

Câu 7:

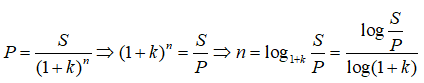
Chọn đáp án A

Câu 8:

log₃100 - log₃18 - log₃50

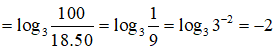
Chọn đáp án B

Câu 9:

(log₂3)(log₉4) = (log₂3) = (log_3²2²) = (log₂3)(log₃2) = 1

Chọn đáp án B

Câu 10:

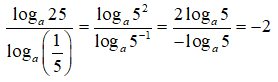
Chọn đáp án A

Câu 11:

Sử dụng công thức a^log_ab

⇒ 10^log7 = 7

Chọn đáp án C

Câu 12:

P = log₃a² + log₃b³ = 2log₃a + 3log₃b

Chọn đáp án B

Câu 13:

P = log₂56 - log₂9 = log₂(8.7) - log₂3² = log₂2³ + log₂7 - 2log₂3 = 3 + log₂7 - 2log₂3 = 3 + a - 2b

Chọn đáp án A

Câu 14;

y = 2^3x ⇔ 3x = log₂y ⇔ x = (1/3)log₂y

Chọn đáp án C

Câu 15:

log₃y = (1/2)log₃u + log₃v + 1 <=> log₃y = log₃u^1/2 + log₃v + log₃3 = log₃(√u.v.3) => y = 3√u.v

Chọn đáp án A

Câu 16:

Ta có: 2^x = (e^ln2)x = e^xln2 = e^kx => k = ln2

Chọn đáp án D

Câu 17:

pH = -log[H⁺] ⇒ [H⁺] = 10^-pH = 10^-8,06 ≈ 8,7.10^-9(mol/L)

Chọn đáp án A

Câu 18:

log125 = log(1000/8) = log1000 - log8 = log10³ - log2³ = 3 - 3log2

Chọn đáp án B

Câu 19:

log_ab².log_bc².log_ca² = (2log_ab)(2log_bc)(2log_ca) = 8log_ab.log_bc.log_ca = 8log_ac.log_ca = 8

Chọn đáp án C

Câu 20:

 

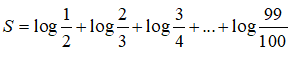
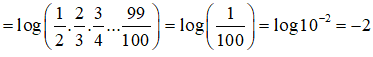
Chọn đáp án D

►►► CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Bộ 20 Câu hỏi trắc nghiệm Toán 12 Lôgarit có đáp án file PDF hoàn toàn miễn phí!