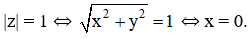Giải Bài tập số phức Toán lớp 12 chi tiết nhất

Để quá trình tiếp thu kiến thức mới trở nên dễ dàng và đạt hiệu quả nhất, trước khi bắt đầu bài học mới các em cần có sự chuẩn bị nhất định qua việc tổng hợp nội dung kiến thức lý thuyết trọng tâm, sử dụng những kiến thức hiện có thử áp dụng giải các bài toán, trả lời câu hỏi liên quan. Dưới đây chúng tôi đã soạn sẵn Lời giải Bài 1: Số phức đầy đủ nhất, giúp các em tiết kiệm thời gian. Nội dung chi tiết được chia sẻ dưới đây.

Bài 1: Số phức

Câu hỏi ứng dụng

Câu hỏi 1 trang 130: 

Tìm phần thực và phần ảo của các số phức sau: -3 + 5i, 4 - i√2, 0 + πi, 1 + 0i.

Hướng dẫn giải chi tiết:

Câu hỏi 2 trang 131: 

Viết số phức z có phần thực bằng 1/2, phần ảo bằng - √3/2.

Hướng dẫn giải chi tiết:

Số phức đó là z = 1/2 - √3/2 i.

Câu hỏi 3 trang 132:

a) Biểu diễn trên mặt phẳng tọa độ các số phức sau: 3 – 2i, -4i, 3.

b) Các điểm biểu diễn số thực, số thuần ảo nằm ở đâu trên mặt phẳng tọa độ ?

Hướng dẫn giải chi tiết:

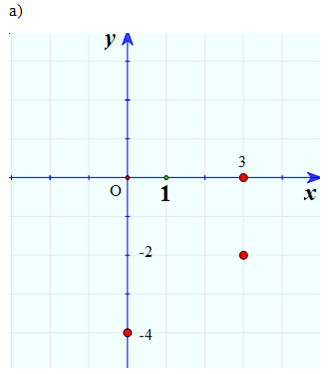
b) Các điểm biểu diễn số thực nằm trên Ox, các điểm biểu diễn số ảo nằm trên Oy.

Câu hỏi 4 trang 132: 

Số phức nào có môđun bằng 0 ?

Hướng dẫn giải chi tiết:

Số phức là môđun bằng 0 là z = 0 + 0i.

Câu hỏi 5 trang 132: 

Biểu diễn các cặp số phức sau trên mặt phẳng tọa độ và nêu nhận xét:

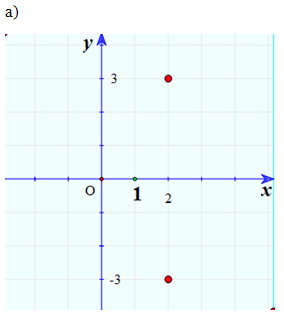
a) 2 + 3i và 2 – 3i;

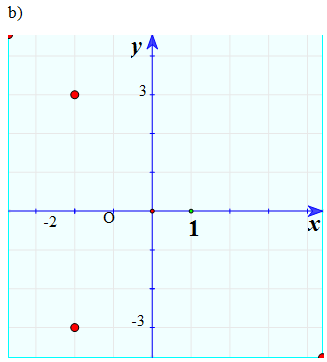
b) -2 + 3i và -2 – 3i.

Hướng dẫn giải chi tiết:

Hai điểm đối xứng nhau qua Ox.

Hai điểm đối xứng nhau qua Oy.

Câu hỏi 6 trang 133: 

Cho z = 3 – 2i.

a) Hãy tính z- và 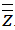. Nêu nhận xét.

b) Tính |z| và |z-|. Nêu nhận xét.

Hướng dẫn giải chi tiết:

Bài tập ứng dụng

Bài 1 (trang 133 SGK Giải tích 12): 

Tính phần thực phần ảo của số phức x, biết:

a) z = 1 - πi

b) z = √2 - i

c) z = 2 √2

d) z = -7i

Hướng dẫn giải chi tiết:

a) Phần thực: 1, phần ảo: -π

b) Phần thực: √2, phần ảo: -1

c) Phần thực: 2 √2, phần ảo: 0

d) Phần thực: 0, phần ảo: -7

Kiến thức áp dụng

+ Mỗi biểu thức có dạng z = a + bi được gọi là một số phức, trong đó:

   a là phần thực

   b là phần ảo.

+ Nếu b = 0 thì z là số thực.

   Nếu a = 0 thì z được gọi là số ảo.  

Bài 2 (trang 133 SGK Giải tích 12): 

Tìm các số thực x và y, biết:

a) (3x - 2) + (2y + 1)i = (x + 1) - (y - 5)i

b) (1 - 2x) - i√3 = √5 + (1 - 3y)i

c) (2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i

Hướng dẫn giải chi tiết:

a) (3x – 2) + (2y – 1).i = (x + 1) – (y – 5).i

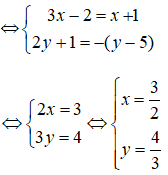
b) (1 - 2x) - i√3 = √5 + (1 - 3y)i

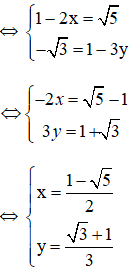
c) (2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i

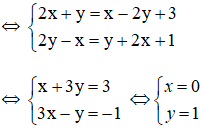
Kiến thức áp dụng

+ Hai số phức z = a + bi và z’ = a’ + b’i bằng nhau :

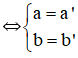
Bài 3 (trang 133 SGK Giải tích 12): 

Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:

a) Phần thực của z bẳng -2

b) Phần ảo của z bẳng 3

c) Phần thực của z thuộc khoảng (-1;2)

d) Phần ảo của z thuộc đoạn [1;3]

e) Phần thực và phần ảo đều thuộc đoạn [-2; 2]

Hướng dẫn giải chi tiết:

a) Tập hợp các điểm thuộc đường thẳng x = -2

b) Tập hợp các điểm thuộc đường thẳng y = 3

c) Tập hợp các điểm thuộc mặt phẳng nằm giữa hai đường thẳng song song x = -1 và x = 2 (hình có gạch sọc)

d) Phần mặt phẳng giới hạn bởi các đường thẳng song song y = 1 và y = 3( kể cả các điểm thuộc hai đường thẳng đó).

e) Các điểm thuộc hình chữ nhật với các cạnh nằm trên các đường thằng x = -2, x = 2 , y = -2, y = 2.

Bài 4 (trang 134 SGK Giải tích 12): 

Tính |z|, với:

a) z = -2 + i √3

b) z = √2- 3i

c) z = -5

d) z = i√3

Hướng dẫn giải chi tiết:

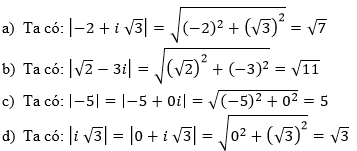
Kiến thức áp dụng

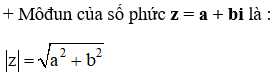
Bài 5 (trang 134 SGK Giải tích 12): 

Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện:

a) |z| = 1

b) |z| ≤ 1

c) 1<|z| ≤ 2

d) |z| = 1 và phần ảo của z = 1

Hướng dẫn giải chi tiết:

Gọi số phức z = x + y.i có điểm biểu diễn là M(x; y).

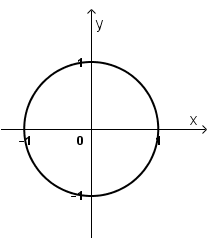
a) |z| = 1 ⇔ √(x² + y² ) = 1 ⇔ x² + y² = 1

Vậy tập hợp điểm M là đường tròn tâm O(0; 0), bán kính R = 1.

b) |z| ≤ 1 ⇔ √(x² + y² ) ≤ 1 ⇔ x² + y² ≤ 1

Vậy tập hợp điểm M là hình tròn tâm O(0; 0), bán kính R = 1.

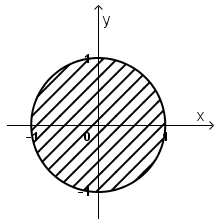
c) 1 < |z| ≤ 2 ⇔ 1 < √(x² + y² ) ≤ 2 ⇔ 1 < x² + y² ≤ 4.

Vậy tập hợp điểm M là hình vành khăn tâm O, bán kính đường tròn nhỏ bằng 1,đường tròn lớn bằng 2, không kể các điểm thuộc đường tròn nhỏ.

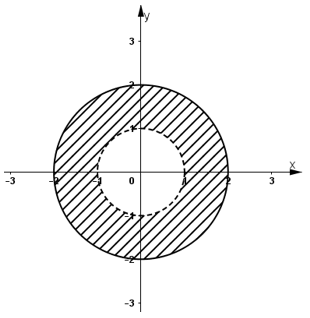
d) Phần ảo của z bằng 1 ⇔ y = 1

Vậy điểm M(0; 1).

Kiến thức áp dụng

+ Số phức z = x + yi được biểu diễn bởi điểm M(x; y) trên mặt phẳng tọa độ Oxy.

Bài 6 (trang 134 SGK Giải tích 12): 

Tìm z, biết:

a) z = 1 - i√2

b) z = -√2 + i√3

c) z = 5

d) z = 7i

Hướng dẫn giải chi tiết:

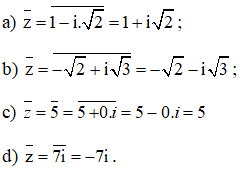
Kiến thức áp dụng

Số phức liên hợp của số phức z = a + bi là:

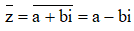
Lý thuyết trọng tâm

A. Tóm tắt lý thuyết

1. Phần thực và phần ảo của số phức, số phức liên hợp.

    a) Số phức z là biểu thức có dạng z = a + bi (a, b ∈ R, i² = -1) . Khi đó:

        + Phần thực của z là a, phần ảo của z là b và i được gọi là đơn vị ảo.

    b) Số phức liên hợp của z là .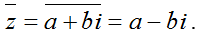

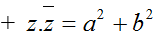
        + Tổng và tích của z và z− luôn là một số thực.

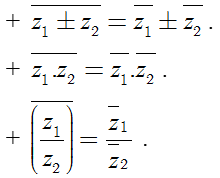
    Đặc biệt:

        + Số phức z = a + 0i có phần ảo bằng 0 được coi là số thực và viết là z = a

        + Số phức z = 0 + bi có phần thực bằng 0 được gọi là số ảo (hay số thần ảo) và viết là

        + Số i = 0 + li = li.

        + Số: 0 = 0 + 0i vừa là số thực vừa là số ảo.

2. Số phức bằng nhau.

        + Cho hai số phức z₁ = a₁ + b₁i, z₂ + b₂i (a₁, a₂, b₁, b₂ ∈ R). Khi đó:

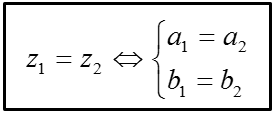
3. Biểu diễn hình học của số phức, mô đun của số phức.

    a) Biễu diễn hình học của số phức.

    + Số phức z = a + bi (a, b ∈ R) được biểu diễn bởi điểm M(a; b) trong mặt phẳng tọa độ.

    + z và z− được biểu diễn bởi hai điểm đối xứng nhau qua trục 0x.

    b) Mô đun của số phức.

    + Mô đun của số phức z là .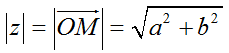

    + 

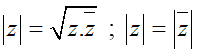
File tải hướng dẫn giải bài tập + lý thuyết Toán 12 Số phức:

Hy vọng tài liệu sẽ hữu ích cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác.

►Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích hỗ trợ ôn luyện thi môn toán như đề kiểm tra học kì, 1 tiết, 15 phút trên lớp, hướng dẫn giải sách giáo khoa, sách bài tập được cập nhật liên tục tại chuyên trang của chúng tôi.