21 Câu hỏi trắc nghiệm Toán 12 Bài 1: Sự đồng biến nghịch biến của hàm số (Có đáp án)

Bộ câu hỏi và bài tập trắc nghiệm Toán 12 Bài 1: Sự đồng biến nghịch biến của hàm số được chúng tôi sưu tầm và tổng hợp bao gồm những dạng câu hỏi trọng tâm và thường xuất hiện trong bài kiểm tra quan trọng. Mời các em học sinh và quý thầy cô giáo theo dõi chi tiết dưới đây.

Bộ 21 bài tập trắc nghiệm Toán 12 Bài 1: Sự đồng biến nghịch biến của hàm số

Câu 1: Cho đồ thị hàm số với x ∈ [- π/2 ; 3π/2] như hình vẽ.

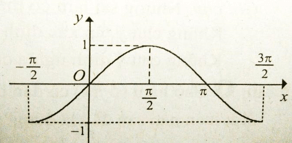
Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- π/2 ; 3π/2]

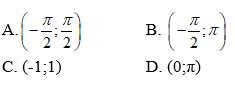
Câu 2: Cho đồ thị hàm số y = -x³ như hình vẽ. Hàm số y = -x³ nghịch biến trên khoảng:

A. (-1;0)     B. (-∞;0)

C. (0;+∞)    D. (-1;1)

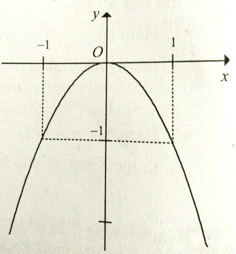
Câu 3: Cho đồ thị hàm số y = -2/x như hình vẽ. Hàm số y = -2/x đồng biến trên

A. (-∞;0)   B. (-∞;0) ∪ (0;+∞)

C. R    D. (-∞;0) và (0;+∞)

Câu 4: Cho hàm số f(x) có đạo hàm f'(x) = √x(x-1)(x+2)²

Kết luận nào sau đây là đúng?

A. Hàm số f(x) nghịch biến trên khoảng (-∞;1).

B. Hàm số f(x) đồng biến trên các khoảng (-∞;0) và (1;+∞).

C. Hàm số f(x) đồng biến trên các khoảng và (1;+∞).

D. Hàm số f(x) đồng biến trên các khoảng (1;+∞).

Câu 5: Khoảng nghịch biến của hàm số y = x³/3 - 2x² + 3x + 5 là:

A. (1;3)    

B.(-∞; 1) ∪ (3; +∞)   

C. (-∞; 1) và (3; +∞)    

D. (1;+∞)

Câu 6: Cho hàm số y = x⁴ - 2x² + 3 . Kết luận nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)

B. Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)

C. Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)

D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)

Câu 7: Cho hàm số y = sin2x - 2x. Hàm số này

A. Luôn đồng biến trên R    

B. Chỉ đồng biến trên khoảng (0; +∞)

C. Chỉ nghịch biến trên (-∞; -1)    

D. Luôn nghịch biến trên R

Câu 8: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?

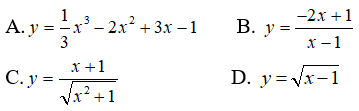
Câu 9: Tìm m để hàm số

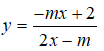
luôn nghịch biến trên khoảng xác định.

A.-2 < m ≤ 2    

B. m < -2 hoặc m > 2

C. -2 < m < 2    

D. m ≠ ±2

Câu 10: Cho hàm số y = -x³ + 3x² + 3mx - 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)

A. m < 1    B. m ≥ 1    C. m ≤ -1    D. m ≥ -1

Câu 11: Cho đồ thị hàm số có dạng như hình vẽ.

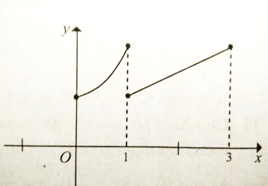
Hàm số đồng biến trên:

A. (0;1)

B. (1;3)

C. (0; 1) ∪ (1; 3)

D. (0;1) và (1;3).

Câu 12: Hỏi hàm số

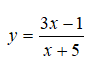
đồng biến trên các khoảng nào?

A. (-∞ ; +∞)    

B. (-∞; -5)

C. (-5; +∞) ∪ (1; 3)    

D. (0; 1) và (1; 3)

Câu 13: Tìm khoảng đồng biến của hàm số y = 2x³ - 9x² + 12x + 3

A.(-∞; 1) ∪ (2; +∞)    

B. (-∞ 1] và [2; +∞)

C. (-∞; 1) và (2; +∞)    

D. (1;2)

Câu 14: Khoảng nghịch biến của hàm số y = x⁴ - 2x² - 1 là:

A. (-∞; -1) và (0; 1)    

B. (-∞; 0) và (1; +∞)

C. (-∞; -1) ∪ (0; 1)    

D. (0;1)

Câu 15: Cho hàm số

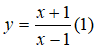
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số (1) nghịch biến trên R\{1}

B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)

C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)

D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)

Câu 16: Tìm khoảng đồng biến của hàm số f(x)= x + cos²x

A. R\{0}    

B. (-∞; +∞)    

C. (-1; 1)   

D. (0; π)

Câu 17: Hàm số:

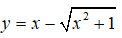
đồng biến trên khoảng nào?

A. R    

B. (-∞; 0)    

C. (-1; 0)    

D. (0; +∞)

Câu 18: Cho hàm số y = x³ - x² + (m-1)x + m. Tìm điều kiện của tham số m để hàm số đồng biến trên R

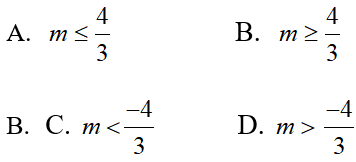
Câu 19: Cho hàm số

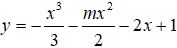
Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).

A. m < 2√2    

B. m ≥ -2√2    

C. m = 2√2    

D. -2√2 ≤ m 2√2

Câu 20: Tìm tất cả các giá trị của tham số m sao cho hàm số

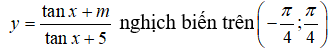
A. 1 < m < 5    

B. m ≥ 5    

C. m < -1 hoặc m > 5    

D. m > 5

Câu 21: 11. Cho hàm số y = x³ + 3x² + mx + 1 - 2m. Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.

A. m =0    

B. m = 1/4    

C. 9/4    

D. Không tồn tại

Đáp án và lời giải câu hỏi trắc nghiệm Toán 12 Bài 1: Sự đồng biến nghịch biến của hàm số

Câu 1:

Trên khoảng (-π/2; π/2) đồ thị hàm số đi lên từ trái sang phải.

Trên khoảng (π/2 ; 3π/2) đồ thị hàm số đi xuống từ trái sang phải.

Do đó hàm số đồng biến trên khoảng (-π/2; π/2)

Chọn đáp án A

Câu 2:

Trên khoảng (0; +∞) đồ thị hàm số đi xuống từ trái sang phải.

Do đó hàm số nghịch biến trên khoảng (0;+∞)

Chọn đáp án C

Câu 3:

Đồ thị hàm số đi lên từ trái sang phải trên hai khoảng (-∞;0) và (0;+∞)

Chọn đáp án D.

Ghi chú. Những sai lầm có thể gặp trong quá trình làm bài:

- Không chú ý tập xác định nên chọn đáp án C.

- Không chú ý định nghĩa của hàm đồng biến

Chọn đáp án B

Câu 4:

Điều kiện: x > 0

Bảng xét dấu :

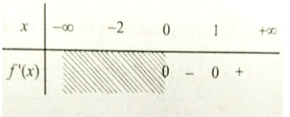
Vậy f(x) đồng biến trên khoảng (1;+∞) và nghịch biến trên khoảng (0;1).

Chọn đáp án D

Câu 5:

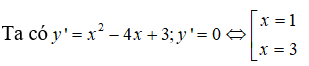
Bảng xét dấu y’ :

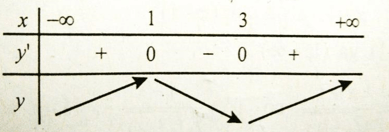
Vậy hàm số nghịch biến trên khoảng (1;3). 

Chọn đáp án A

Câu 6:

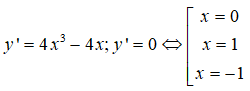
Bảng xét dấu y’:

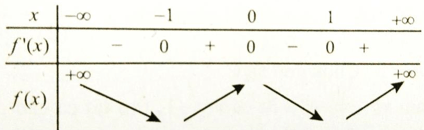
Từ đó ta có: Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞) , nghịch biến trên các khoảng (-∞; -1) và (0; 1) . 

Chọn đáp án D

Câu 7:

Tập xác định D = R

Ta có : y' = 2.cos2x - 2 = 2(cos2x - 1) ≤ 0; ∀ x

(vì -1 ≤ cos2x ≤ 1)

Vậy hàm số luôn nghịch biến trên R

Chọn đáp án D

Câu 8:

Chọn đáp án C

Câu 9:

Tập xác định

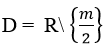
Hàm số nghịch biến trên từng khoảng

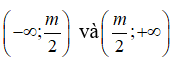
khi và chỉ khi

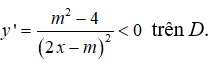
Suy ra m² - 4 < 0 hay -2 < m < 2.

Chọn đáp án C

Câu 10:

Ta có y' = -3x² + 6x + 3m. Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)

Cách 1: Dùng định lí dấu tam thức bậc hai.

Xét phương trình -3x² + 6x + 3m. Ta có Δ' = 9(1 + m)

TH1: Δ' ≤ 0 => m ≤ -1 khi đó, -3x² + 6x + 3m < 0 nên hàm số nghịch biến trên R .

TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .

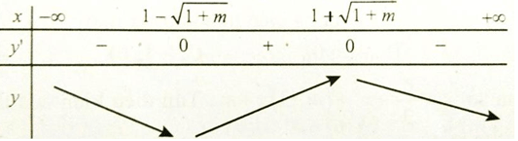
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.

Từ TH1 và TH2, ta có m ≤ -1

Cách 2: Dùng phương pháp biến thiên hàm số.

Ta có y' = -3x² + 6x + 3m ≤ 0, ∀x > 0 <=> 3m ≤ 3x² - 6x, ∀x > 0

Từ đó suy ra 3m ≤ min(3x² - 6x) với x > 0

Mà 3x² -6x = 3(x² -2x + 1) - 3 = 3(x - 1)² - 3 ≥ -3 ∀ x

Suy ra: min( 3x² – 6x) = - 3 khi x= 1

Do đó 3m ≤ -3 hay m ≤ -1.

Chọn đáp án C

Câu 11:

Trên khoảng (0; 1) đồ thị hàm số đi lên từ trái qua phải

Trên khoảng (1; 3) đồ thị hàm số đi lên từ trái qua phải

Đồ thị hàm số bị gián đoạn tại x = 1. Do đó hàm số đồng biến trên từng khoảng (0; 1) và (1; 3)

Chọn đáp án C

Câu 12:

Hàm số xác định ∀x ≠ -5

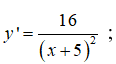
y' xác định ∀x ≠ -5 . Bảng xét dấu y’:

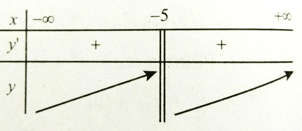
Vậy hàm số đồng biến trên các khoảng (-∞; -5) và (-5; +∞)

Chọn đáp án A

Câu 13:

Ta có

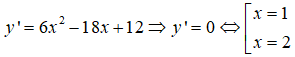
Bảng xét dấu đạo hàm:

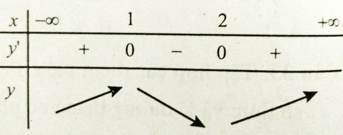
Hàm số đồng biến trên các khoảng (-∞; 1) và (2; +∞)

Chọn đáp án C

Câu 14:

Ta có

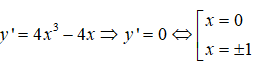
Bảng xét dấu đạo hàm

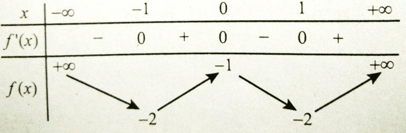
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)

Chọn đáp án A

Câu 15:

Hàm số

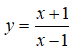
xác định ∀x ≠ 1

Ta có:

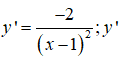
xác định ∀x ≠ 1

Bảng xét dấu đạo hàm

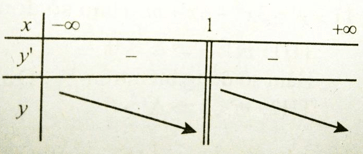
Hàm số nghịch biến trên các khoảng (-∞ 1) và (1; +∞)

Chọn đáp án B

Câu 16:

f'(x) = 1 - 2sinxcosx = sin²x + cos²x - 2.sinx.cosx = (sinx - cosx)² ≥ 0 ∀x ∈ R

Hàm số đồng biến trên khoảng (-∞; +∞)

Chọn đáp án B

Câu 17:

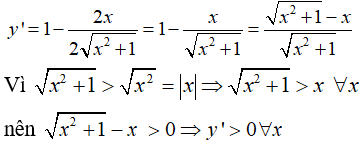
Hàm số đồng biến trên R

Chọn đáp án A

Câu 18:

Ta có: y’ = 3x² – 2x + m – 1

Để hàm số đã cho đồng biến trên R khi và chỉ khi y' ≥ 0 với mọi x.

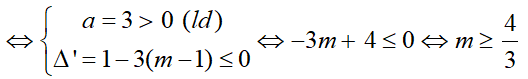
Chọn đáp án B

Câu 19:

Ta có y' = -x² - mx - 2 . Hàm số nghịch biến trên khoảng (-∞; - 1) nếu y' = x² - mx - 2 ≤ 0 trên khoảng (-∞; -1)

Cách 1. Dùng định lí dấu của tam thức bậc hai. Ta có Δ = m² - 8

TH1: -2√2 ≤ m ≤ 2√2 => Δ ≤ 0.

Lại có, hệ số a= -1 < 0 nên y' ≤ 0 ∀ x

Hàm số nghịch biến trên R

TH2: 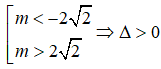 y' = 0. có hai nghiệm phân biệt là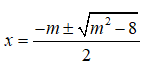 

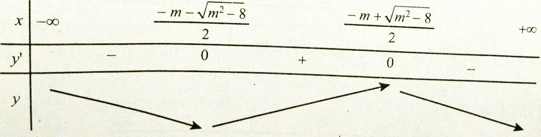
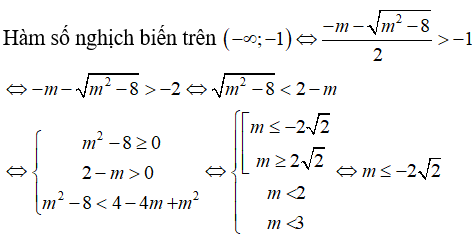
Từ TH1 và TH2, ta có m ≤ 2√2

Cách 2. Dùng phương pháp biến thiên hàm số

Ta có

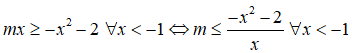
Từ đó suy ra

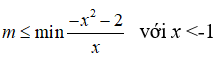
Do đó m ≤ 2√2

Vậy giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1) là m = 2√2

Chọn đáp án C

Câu 20:

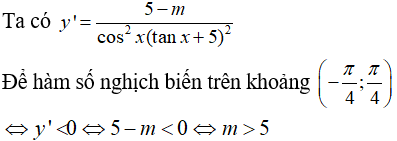
Chọn đáp án D

Câu 21:

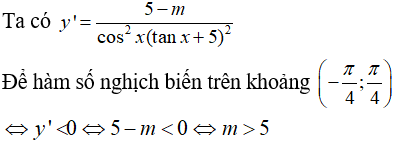
y' = 3x² + 6x + m. Hàm số đồng biến nếu y' ≥ 0. Ta có Δ' = 9 - 3m

TH1: m ≥ 3 => Δ' ≤ 0 .

Hàm số đồng biến trên R. Do đó m ≥ 3 không thỏa mãn yêu cầu đề bài

TH2: m < 3 => Δ' > 0 .

y’ có hai nghiệm phân biệt là

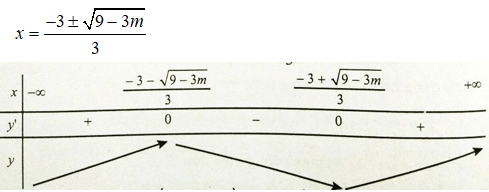
Từ bảng biến thiên, ta thấy không tồn tại m để hàm số đồng biến trên đoạn có độ dài bằng 1.

Từ TH1 và TH2, không tồn tại m thỏa mãn.

Chọn đáp án D

►►► CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Bộ 21 Câu hỏi trắc nghiệm Toán 12 Bài 1: Sự đồng biến nghịch biến của hàm số có đáp án file PDF hoàn toàn miễn phí!