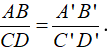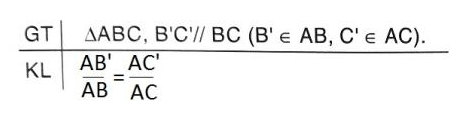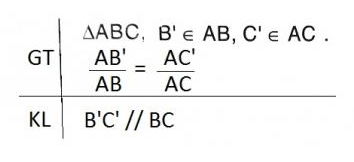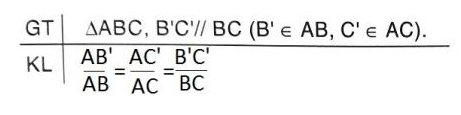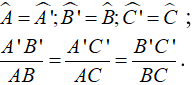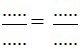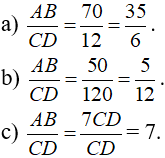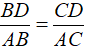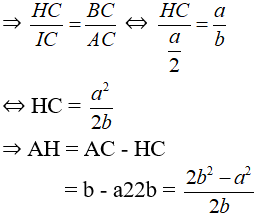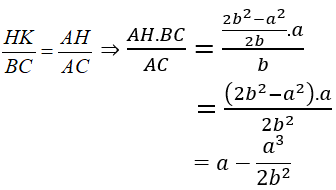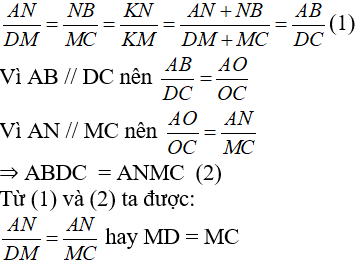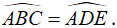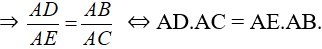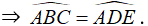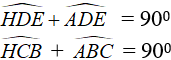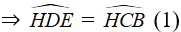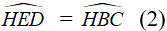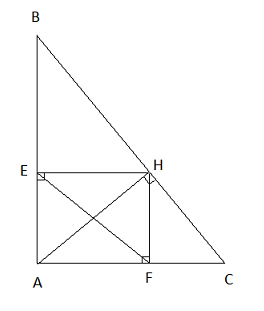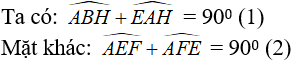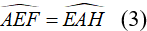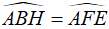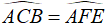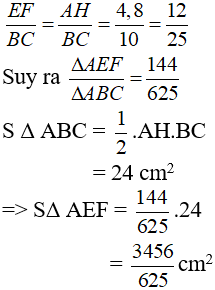Giải Toán lớp 8 VNEN Bài 9: Ôn tập chương III

Hướng dẫn giải bài tập Toán lớp 8 VNEN Bài 9: Ôn tập chương III chi tiết, dễ hiểu được biên soạn bởi đội ngũ chuyên gia giàu kinh nghiệm chia sẻ. Hy vọng đây sẽ là tài liệu hữu ích hỗ trợ học sinh trong quá trình học tập. Mời các em tham khảo tại đây.

Giải Toán 8 VNEN Bài 9: Hoạt động luyện tập

Câu 1 (Trang 80 Toán 8 VNEN Tập 2)

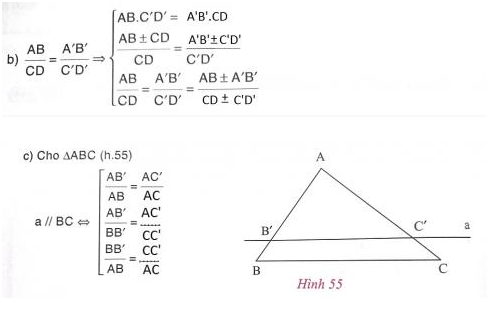
(1) Phát biểu và viết tỉ lệ thức biểu thị hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng A'B' và C'D'.

(2) Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta-lét trong tam giác.

(3) Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta-lét đảo.

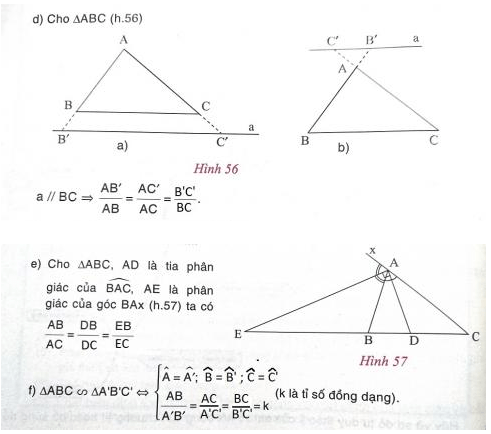
(4) Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Ta-lét.

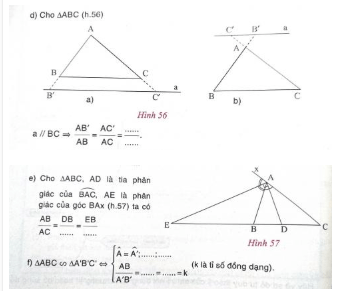
(5) Phát biểu định lí về tính chất của đường phân giác trong tam giác (vẽ hình, ghi giả thiết và kết luận).

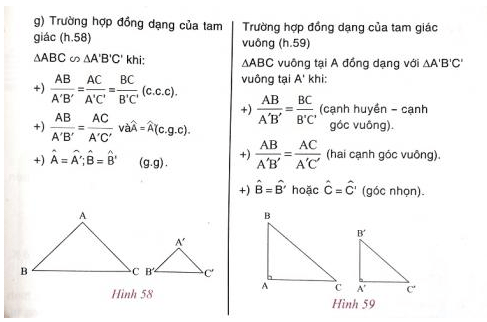
(6) Thế nào là hai tam giác đồng dạng.

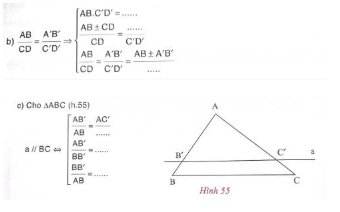
(7) Phát biểu định lí về đường thẳng song song với một cạnh của tam giác và cắt hai cạnh (hoặc phần kéo dài của hai cạnh) còn lại.

(8) Nêu các trường hợp đồng dạng của hai tam giác.

(9) Nêu trường hợp đồng dạng đặc biệt của hai tam giác vuông (trường hợp cạnh huyền và một cạnh góc vuông).

Lời giải:

(1) Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng đơn vị do.

(2) Định lí Ta-lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

(3) Định lí Ta-lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

(4) Hệ quả của định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

(5) Định lí về tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy

(6) Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:

(7) Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

(8) Có ba trường hợp đồng dạng của tam giác:

- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng

- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng

- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

(9) Nếu một cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt tỉ lệ với một cạnh huyền và một cạng góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng.

Câu 2 (Trang 82 Toán 8 VNEN Tập 2)

a) Đoạn thẳng AB, CD tỉ lệ với A'B', C'D' ⇔ 

Lời giải:

a) Đoạn thẳng AB, CD tỉ lệ với A'B', C'D' ⇔ ABA′B′ = CDC′D′

I. BÀI TẬP LUYỆN TẬP

Câu 1 (Trang 83 Toán 8 VNEN Tập 2)

Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau:

a) AB = 7dm, CD = 12cm;

b) AB = 50cm, CD = 12dm;

c) AB = 7CD.

Lời giải:

Câu 2 (Trang 83 Toán 8 VNEN Tập 2)

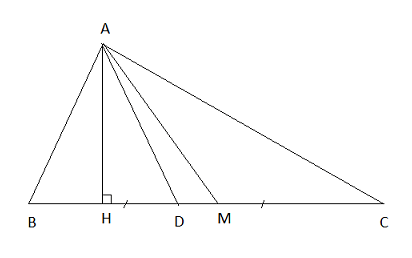
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Trong ba điểm H, D, M điểm nào nằm giữa hai điểm còn lại? Vì sao?

Lời giải:

Δ AMB và ΔAMC có: AM chung MB = MC và AC > AB

 => M thuộc CH (M ở giữa C và H)

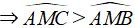
Ta có: AB < AC ⇒ Bˆ > Cˆ ⇒ 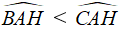 ⇒ D thuộc CH (1)

Theo tính chất đường phân giác:

Mặt khác: AC > AB => CD > BD => D thuộc BM (2)

Từ (1) và (2) ⇒ D thuộc HM hay D là điểm nằm giữa H và M.

Câu 3 (Trang 83 Toán 8 VNEN Tập 2)

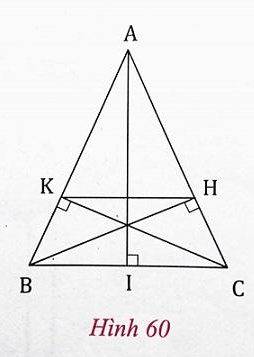
Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h,60). Chứng minh:

a) Tìm các cặp tam giác đồng dạng có trong hình và giải thích.

b) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.

Hướng dẫn câu b):

- Vẽ thêm đường cao AI, xét hai tam giác đồng dạng IAC và HBC rồi tính CH.

- Tiếp theo, xét hai tam giác đồng dạng AKH và ABC rồi tính HK.

Lời giải:

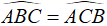
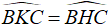
a) * Δ KCB và Δ HBC có  (do tam giác ABC cân),, BC chung nên

Δ KCB = Δ HBC

⇒ BK = HC ⇒ AK = AH

* Δ AKH và Δ ABC có góc A chung, 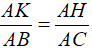 nên Δ AKH ∼ Δ ABC

* Gọi giao điểm của BH và CK là O

Vì 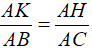 nên KH // BC

Δ OKH và Δ OCB có 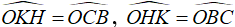 (so le trong) nên Δ OKH ∼ Δ OCB.

b) Vẽ đường cao AI

Δ IAC và Δ HBC có góc C chung, 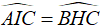 nên Δ IAC ∼ Δ HBC

Theo câu a) Δ AKH ∼ Δ ABC nên

Câu 4 (Trang 83 Toán 8 VNEN Tập 2)

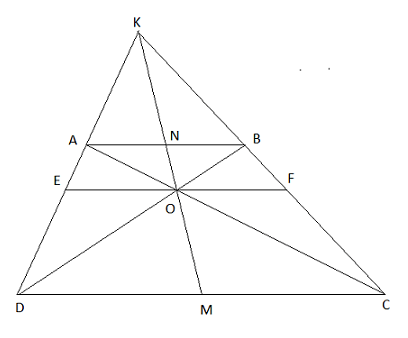
Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.

Lời giải:

Tứ giác ABCD là hình thang nên AB//CD

Gọi N, M lần lượt là giao điểm của KO với AB,CD.

Áp dụng định lý talet ta có:

Tương tự ta được: NA = NB

Vậy OK đi qua trung điểm của AB và CD.

Giải Toán VNEN lớp 8 Bài 9: Hoạt động vận dụng và tìm tòi mở rộng

Câu 1 (Trang 84 Toán 8 VNEN Tập 2)

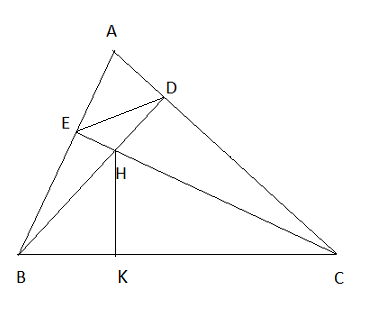
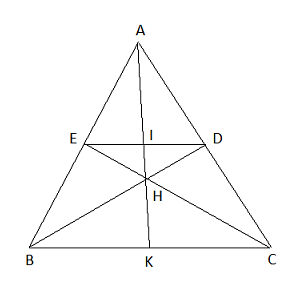
Cho tam giác ABC nhọn, đường cao BD, CE cắt nhau tại H.

a) Chứng minh rằng AD.AC = AE.AB và 

b) Chứng minh rằng Δ HED và Δ HBC đồng dạng.

c) Chứng minh rằng BE.BA + CD.CA = BC².

d) Nếu Δ ABC đều hãy tính tỉ số diện tích Δ HED và diện tích Δ ABC.

Lời giải:

a) * Δ ADB và Δ AEC có góc A chung, 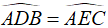 nên Δ ADB ∼ Δ AEC

* Δ ADE và Δ ABC có góc A chung, ADAE = ABAC nên Δ ADE ∼ Δ ABC.

b)

Ta có:

Mặt khác 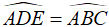 (theo câu a) 

Tương tự ta được 

Từ (1) và (2) suy ra Δ HED ∼ Δ HBC

c) Dựng HK vuông góc với BC

Ta có:

Δ BKH ∼ Δ BDC nên 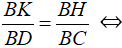 BK.BC = BH.BD

Δ CKH ∼ Δ CEB nên 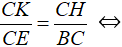 CK.BC = CH.CE

⇒ BK.BC + CK.BC = BH.BD + CH.CE ⇔ BC.(BK + CK) = BH.BD + CH.CE ⇔ BC² = BH.BD + CH.CE

Ta có: Δ BEH ∼ Δ BDA nên: 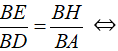 BH.BD = BE.BA

Tương tự ta được CH.CE = CD.CA

Suy ra BC² = BE.BA + CD.CA.

d)

Câu 2 (Trang 84 Toán 8 VNEN Tập 2)

Cho Δ ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và AC.

a) Chứng minh rằng: Δ AEF Δ ABC.

b) Cho AH = 4,8cm; BC = 10cm. Tính SΔAEF?

c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy tại một điểm.

Lời giải:

a) Gọi giao điểm của EF và AH là I

Tứ giác AEHF là hình chữ nhật nên: 

Từ (1), (2),(3) suy ra: 

Tương tự ta có: 

Suy ra Δ AEF ∼ Δ ACB.

b) Tứ giác AEHF là hình chữ nhật nên AH = EF

Ta có tính chất: Tỉ lệ diện tích hai tam giác bằng bình phương tỉ lệ đồng dạng của hai tam giác đó

Tỉ lệ đồng dạng của Δ AEF và Δ ABC là:

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán lớp 8 VNEN Tập 2 Bài 9: Ôn tập chương III file PDF hoàn toàn miễn phí.