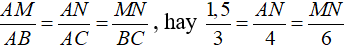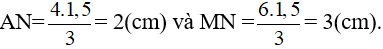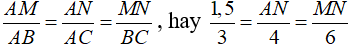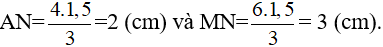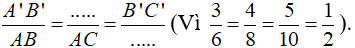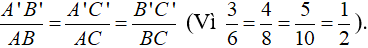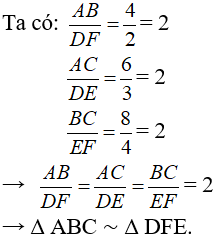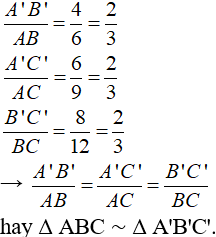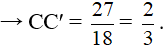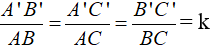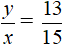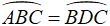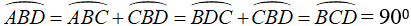Giải Toán lớp 8 VNEN Bài 5: Trường hợp đồng dạng thứ nhất

Hướng dẫn giải bài tập Toán lớp 8 VNEN Bài 5: Trường hợp đồng dạng thứ nhất chi tiết, dễ hiểu được biên soạn bởi đội ngũ chuyên gia giàu kinh nghiệm chia sẻ. Hy vọng đây sẽ là tài liệu hữu ích hỗ trợ học sinh trong quá trình học tập. Mời các em tham khảo tại đây.

Giải Toán 8 VNEN Bài 5: Hoạt động khởi động và hình thành kiến thức

Câu 1 (Trang 65 Toán 8 VNEN Tập 2)

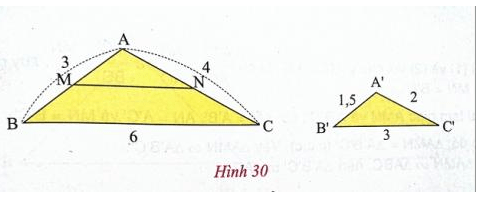
1. a) Cho ΔABC và Δ A'B'C' có các kích thước như hình 30 (cùng đơn vị đo là cen-ti-met). Hỏi Δ ABC và Δ A'B'C' có đồng dạng với nhau không?

Điền vào chỗ trống (...) để hoàn thiện

- Lấy M trên AB sao cho AM = 1,5cm.Qua M kẻ đường thẳng song song với BC cắt cạnh AC tại N.

- Vì MN // BC nên Δ AMN ∼ Δ......

Suy ra 

nên 

Vậy Δ AMN = Δ........(AM = A'B'; AN =.........; MN = .........).

Suy ra Δ AMN ∼ .........

Từ (1) và (2) suy ra Δ ABC ∼ Δ A'B'C'.

Lời giải:

- Lấy M trên AB sao cho AM = 1,5cm.Qua M kẻ đường thẳng song song với BC cắt cạnh AC tại N.

- Vì MN // BC nên Δ AMN ∼ Δ ABC

Suy ra 

nên 

Vậy Δ AMN = Δ A'B'C' (AM = A'B'; AN = A'C'; MN = B'C').

Suy ra Δ AMN ∼ A'B'C'

Từ (1) và (2) suy ra Δ ABC ∼ Δ A'B'C'.

Câu 2 (Trang 66 Toán 8 VNEN Tập 2)

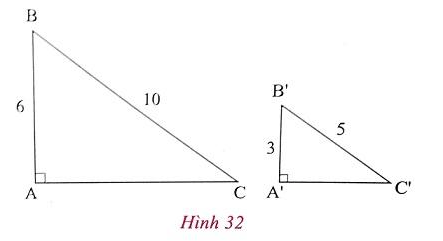
a) Cho hình 32, độ dài các cạnh cho trên hình vẽ ( có cùng đơn vị đo cen-ti-met).

* Tính AC và A'C'.

* Chứng tỏ Δ A'B'C' ∼ Δ ABC.

Điền vào chỗ trống (...) để hoàn thiện lời giải

* Áp dụng định lí Py-ta-go vào Δ A'B'C' vuông tại A', có:

A′B′² + A′C′² = B′C′² hay A′C′² = ...........suy ra A'C' = 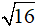 = ........(cm).

Áp dụng định lí Py-ta-go vào Δ ABC vuông tại A, có:

AB² + AC² = BC² hay AC² = ...........suy ra AC =............ = 8 (cm).

* Δ A'B'C' và Δ ABC, có: 

Vậy Δ ABC ∼ Δ.........

Lời giải:

* Áp dụng định lí Py-ta-go vào Δ A'B'C' vuông tại A', có:

A′B′² + A′C′² = B′C′² hay A′C′² = 16 suy ra A'C' = 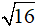 = 4(cm).

Áp dụng định lí Py-ta-go vào Δ ABC vuông tại A, có:

AB² + AC² = BC² hay AC² = 64 suy ra AC = 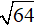 = 8 (cm).

* Δ A'B'C' và Δ ABC, có: 

Vậy Δ ABC ∼ Δ A'B'C'.

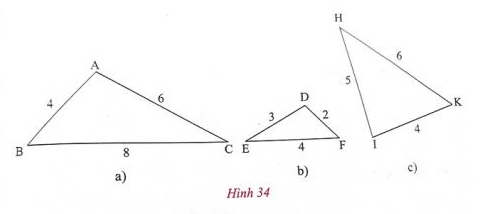
d) Tìm trong hình 34 các cặp tam giác đồng dạng:

Lời giải:

Giải Toán VNEN lớp 8 Bài 5: Hoạt động luyện tập

Câu 1 (Trang 67 Toán 8 VNEN Tập 2)

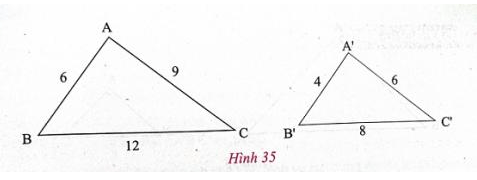
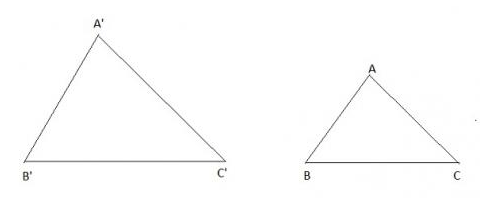
Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35.

a) Δ ABC và Δ A'B'C' có đồng dạng vói nhau không? Vì sao?

b) Tính tỉ số chu vi của hai tam giác đó.

Lời giải:

a) Ta có:

b) Chu vi tam giác ABC là C = 6 + 9 + 12 = 27

Chu vi tam giác A'B'C' là C' = 4 + 6 + 8 = 18

Câu 2 (Trang 5 Toán 8 VNEN Tập 2)

Tam giác ABC có độ dài các cạnh là AB = 3cm, AC = 4cm, BC = 8cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 45cm. Hãy tính độ dài các cạnh của tam giác A'B'C'.

Lời giải:

Gọi tỉ số đồng dạng giữa tam giác A'B'C' và tam giác ABC là k

Ta có: 

Suy ra: A'B' = k.AB = 3k, A'C' = k.AC = 4k, B'C' = k.BC = 8k

Theo bài ra ta có chu vi tam giác A'B'C' là 45

Tức là 3k + 4k + 8k = 45

⇔ 15k = 45

⇔ k = 3

Suy ra: A'B' = 3.3 = 9 cm

A'C' = 4.3 = 12 cm

B'C' = 8.3 = 24 cm

Câu 3 (Trang 68 Toán 8 VNEN Tập 2)

Cho hai tam giác đồng dạng có tỉ số chu vi là 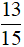 và hiệu độ dài hai cạnh tương ứng của chúng là 14,6 cm. Tính độ dài hai cạnh đó.

Lời giải:

Theo câu 2 ta có: tỉ số chu vi chính là tỉ số đồng dạng

Gọi độ dài hai cạnh là x và y (x > y)

Theo bài ra ta có 

Mặt khác x - y = 14,6 → y = x - 14,6

 ⇔ x = 109,5 → y = 94,9

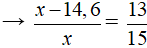
Vậy độ dài hai cạnh lần lượt là 94,9 và 109,5.

Giải SGK Toán 8 VNEN Bài 5: Hoạt động vận dụng

(Trang 68 Toán 8 VNEN Tập 2)

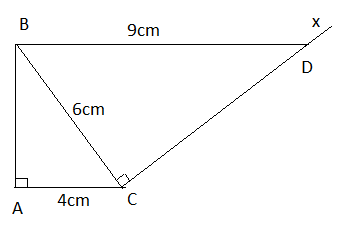
Cho tam giác ABC vuông tại A, AC = 4cm; BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía với đường thẳng BC). Lấy trên Cx điểm D sao cho BD = 9cm (h,36). Chứng minh BD // AC.

Lời giải:

Ta có:

Δ ABC ∼ Δ CDB (tam giác vuông) nên 

Ta có: 

⇒ AC // BD.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán lớp 8 VNEN Tập 2 Bài 5: Trường hợp đồng dạng thứ nhất file PDF hoàn toàn miễn phí.