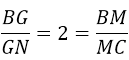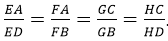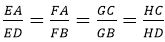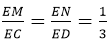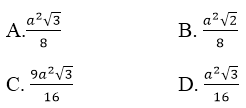26 câu hỏi trắc nghiệm Hình lớp 11: Đường thẳng song song với mặt phẳng
Để giúp các em học sinh lớp 11 học tập hiệu quả môn Toán, chúng tôi đã tổng hợp bộ 26 câu trắc nghiệm Toán hình 11: Đường thẳng song song với mặt phẳng có đáp án và hướng dẫn giải chi tiết, hỗ trợ các em rèn luyện kỹ năng giải Toán một cách nhanh và chính xác nhất. Mời các em học sinh và thầy cô tham khảo tài liệu: 26 câu trắc nghiệm Toán 11: Đường thẳng song song với mặt phẳng tại đây.
Bộ 26 câu trắc nghiệm hình 11: Đường thẳng song song với mặt phẳng
Câu 1:
Với điều kiện nào sau đây thì đường thẳng a song song với mặt phẳng (∝) ?
A. a // b và b ∩ (∝) = ∅
B. a // b và b // (∝)
C. a // b và b ⊂ (∝)
D. a ∩ (∝) = ∅
Đáp án: D
Các phương án A, B, C sai vì ∝ có thể thuộc (∝). Phương án D đúng vì theo định nghĩa. Đáp án D.
Câu 2:
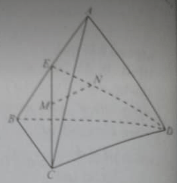
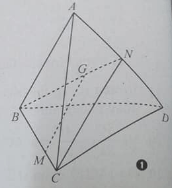
Cho tứ diện ABCD, M, N lần lượt là trọng tâm của tam giác ABC, ABD. Những khẳng định nào sau đây là đúng?
(1) MN //(BCD)
(2) MN //(ACD)
(3) MN // (ABD)
A. Chỉ có (1) đúng
B. (2) và (3)
C. (1) và (2)
D. (1) và (3)
Đáp án: C
Gọi E là trung điểm của AB, M, N lần lượt là trọng tâm của các tam giác ABC, ABD nên:
Theo định lí Ta – lét ta có: MN // CD. Vậy MN // (BCD), MN // (ACD). Đáp án C.
Câu 3:
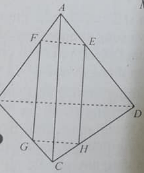
Cho tứ diện ABCD, điểm M thuộc AC. Mặt phẳng (∝) đi qua M, song song với AB và AD. Thiết diện (∝) với tứ diện ABCD là hình gì?
A. Thiết diện là tam giác
B. Hình bình hành
C. Hình thoi
D. Hình thang
Đáp án: A
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua M, song song với AB cắt BC tại P.
(∝) // AD nên giao tuyến của (∝) với (ADC) là đường thẳng qua M, song song với AD, cắt DC tại N.
Vậy thiết diện là tam giác MNP. Đáp án A
Câu 4:
Cho tứ diện ABCD. Giả sử M thuộc đoạn BC. Một mặt (∝) qua M song song với AB và CD. Thiết diện của (∝) và hình tứ diện ABCD là hình gì?
A. Hình thang có đúng một cặp cạnh song song
B. Hình bình hành
C. Hình tam giác
D. Hình ngũ giác
Đáp án: B
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng đi qua M, song song với AB và cắt AC tại Q.
(∝) // CD nên giao tuyến của (∝) với (BCD) là đường thẳng đi qua N, song song với CD và cắt BD tại N.
(∝) // AB nên giao tuyến của (∝) với (ABD) là đường thẳng đi qua N, song song với AB và cắt AD tại P.
Ta có: MN // PQ // CD, MQ // PN // AB.
Vậy thiết diện là hình bình hành MNPQ. Đáp án B.
Câu 5:
Có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng ?
A. 1
B. 2
C. 3
D. 4
Đáp án: C
Câu 6:
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ?
A. 1
B. 2
C. không
D. vô số
Đáp án: A
Câu 7:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây?
A. AC
B. BD
C. AD
D. SC
Đáp án: C
Câu 8:
Cho hình chóp S.ABCD, M, N, P, Q lần lượt là trọng tâm các tam giác SAB, SBC, SCD, SDA. Khẳng định nào sau đây là đúng?
A. MNPQ là hình bình hành.
B. MNPQ là hình thoi.
C. MNPQ là hình thang chỉ có một cặp cạnh đối song song.
D. MNPQ là tứ giác không có cặp cạnh nào song song.
Đáp án: A
Câu 9:
Cho tứ diện đều ABCD cạnh a. I, J lần lượt là trung điểm của AC và BC. Gọi K là giao điểm trên cạnh BD với KB = 2KD. Thiết diện của tứ diện với mặt phẳng (IJK) là hình gì?
A. thiết diện là hình thang cân.
B. hình bình hành.
C. tam giác.
D. tứ giác không có cặp cạnh nào song song.
Đáp án: A
I, J lần lượt là trung điểm của AC và BC nên IJ // AB. Do đó giao tuyến của (IJK) với (ABD) là đường thẳng đi qua K và song song với AB cắt AD tại H. Vậy IJ // KH // AB. Ta có ∆BJK = ∆AIH ⇒ JK = IH. Hơn nữa KH ≠ IJ.
Vậy thiết diện là hình thang cân IJKH.
Câu 10:
Cho hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) sẽ:
A. song song với hai đường thẳng đó
B. song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
C. trùng với một trong hai đường thẳng đó
D. cắt một trong hai đường thẳng đó
Đáp án: B
Câu 11:
Cho tứ diện ABCD. Gọi IJ lần lượt là trung điểm của BC và BD. Giao tuyến của hai mặt phẳng (AIJ) và (ACD) là đường nào sau đây?
A. đường thẳng d đi qua A và d // BC.
B. đường thẳng d đi qua A và d // BD.
C. đường thẳng d đi qua A và d // CD.
D. đường thẳng d đi qua A, M trong đó M là giao điểm IJ và CD.
Đáp án: C
Câu 12:
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm của các tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Trong các mệnh đề sau, mệnh đề nào đúng?
A. IJ // (SBD)
B. IJ // (SEF)
C. IJ // (SAB)
D. IJ // (SAD)
Đáp án: A
Câu 13:
Cho hình chóp S.ABCD đấy ABCD là hình bình hành tâm O. gọi M, N lần lượt là trung điểm của SA và SB. Giao tuyến của hai mặt phẳng (MNC) và (ABD) là đường nào trong các đường thẳng sau đây?
A. OA
B. OM
C. OC
D. CD
Đáp án: D
Câu 14:
Cho hình chóp S.ABCD đấy ABCD là hình bình hành tâm O. gọi M, N lần lượt là trung điểm của SA và SB. Giao tuyến của hai mặt phẳng (MNO) và (ABCD) là đường nào trong các đường thẳng sau đây?
A. OA
B. OM
C. ON
D. đường thẳng d qua O và d // AB
Đáp án: D
Câu 15:
Cho đường thẳng d song song với mặt phẳng (∝), mặt phẳng (β) chứa d và cắt (∝) theo giao tuyến d’. Khẳng định nào sau đây là đúng ?
A. d’ // d hoặc d’ ≡ d
B. d’ // d
C. d’ ≡ d
D. d’ và d chéo nhau
Đáp án: B
Câu 16:
Cho tứ diện ABCD. Lấy M là một điểm thuộc miền trong của tam giác ABC. Gọi (∝) là mặt phẳng qua M và song song với các đường thẳng AB và CD. Thiết diện tạo bởi (∝) và tứ diện ABCD là hình gì?
A. tam giác
B. hình thoi
C. hình bình hành
D. hình ngũ giác
Đáp án: C
Câu 17:
Cho hai đường thẳng a, b và mặt phẳng (∝). Giả sử a // b và b // (∝). Kết luận về vị trí tương đối của a và (∝) nào sau đây là đúng?
A. a // (∝)
B. a ⊂ (∝)
C. a // (∝) hoặc a ⊂ (∝)
D. không xác định
Đáp án: C
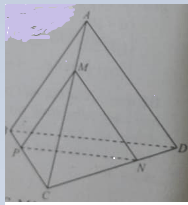
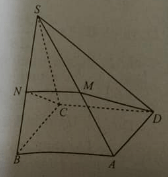
Câu 18:
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?
A. MG // (ACD)
B. MG // (ABC)
C. MG // AB
D. MG cắt AC
Đáp án: A
(hình 1) G là trọng tâm của tam giác ABD nên:
⇒ MG // CN.
Do CN thuộc (ACD) nên MG // (ACD).
Câu 19:
Cho tứ diện ABCD, các điểm E, F, G, H lần lượt thuộc các cạnh AD, AB, BC, CD sao cho
Khẳng định nào sau đây là đúng?
A. EFGH là hình bình hành.
B. EFGH có đúng một cặp cạnh song song.
C. EFGH là tứ giác không có cặt cạnh nào song song.
D. EFGH là hình chữ nhật.
Đáp án: A
(hình 2)
⇒ FG // EH // AC, EF // GH // BD
Vậy EFGH là hình bình hành
Câu 20:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M là trung điểm của SA. Thiết diện của mặt phẳng (MCD) với hình chóp S.ABCD là hình gì?
A. tam giác
B. hình bình hành
C. hình thang
D. hình thoi
Đáp án: C
Vì CD ⊂ (MCD), CD // AB, AB ⊂ (SAB) nên giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB. Vậy MN // CD. Hơn nữa MN ≠ CD. Vậy thiết diện là hình thang CNMD.
Câu 21:
Cho hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng, có tâm lần lượt là O và O’. Chọn khẳng định đúng trong các khẳng định sau:
A. OO’ // (ABCD)
B. OO’ // (ABEF)
C. OO’ // (BDF)
D. OO’ / /(ADF)
Đáp án: D
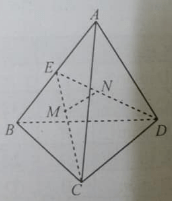
Câu 22:
Cho tứ diện ABCD. Hai điểm M, N lần lượt là trung điểm của AC, AD. Mặt phẳng (∝) chứa MN và song song với AB. Thiết diện của (∝) với tứ diện ABCD là:
A. hình thang
B. hình bình hành
C. hình chữ nhật
D. hình vuông
Đáp án: B
Câu 23:
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. khi đó ta có.
A. MN // (SCD)
B. EF // (SAD)
C. NF // (SAD)
D. IJ // (SAB)
Đáp án: D
Câu 24:
Cho tứ diện ABCD. M, N lần lượt là trọng tâm của các tam giác ABC, ABD. Thiết diện của tứ diện với mặt phẳng (∝) chứa MN và song song với AB là hình gì?
A. tam giác
B. hình bình hành
C. hình thoi
D. hình thang có đúng một cặp cạnh song song
Đáp án: B
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua M, song song với AB, cắt BC tại Q, cắt AC tại G
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua M, song song với AB, cắt BD tại P, cắt AD tại F
Gọi E là trung điểm của AB. M, N lần lượt là trọng tâm các tam giác ABC, ABD nên
theo định lí Ta- lét ta có MN // CD.
Do MN // CD nên PQ // GF // CD, lại có QG // FP nên thiết diện là hình bình hành GQPF.
Câu 25:
Hình chóp S.ABCD có đáy là hình bình hành ABCD. Giả sử M thuộc đoạn thẳng SB. Mặt phẳng (ADM) cắt hình chóp S.ABCD theo thiết diện là hình:
A. tam giác
B. hình thang
C. hình bình hành
D.hình thoi
Đáp án: B
(hình 1) Do AD//BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC, đường thẳng này cắt SC tại N.
Ta có MN//AD. Vậy thiết diện là hình thang AMND.
Câu 26:
Cho tứ diện đều ABCD có cạnh bằng a, điểm M là trung điểm của AB. Tính diện tích thiết diện của hình tứ diện cắt bởi mặt phẳng đi qua M và song song với mặt phẳng (ACD).
Đáp án: D
CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn trả lời bộ 26 câu hỏi trắc nghiệm Toán hình 11 Đường thẳng song song với mặt phẳng file word, pdf hoàn toàn miễn phí.
- Giải Toán Đại 11: Quy tắc tính đạo hàm đầy đủ nhất
- Giải bài tập Toán lớp 11: Ôn tập chương 3 (Đại số) đầy đủ nhất
- Giải bài tập Toán 11: Ôn tập chương 3 (Phần hình học)
- Giải bài tập Toán Lớp 11 trang 92 Bài 2: Dãy số chi tiết nhất
- 66+ Bài tập quy tắc cộng và quy tắc nhân lớp 11 có lời giải
- Soạn Toán 11 Bài 1: Phương pháp quy nạp toán học đầy đủ nhất
- Giải toán lớp 11 trang 103, 104 SGK tập 1: Cấp số nhân
- Giải Toán hình 11 trang 71 SGK tập 2: Hai mặt phẳng song song