Giải bài tập Toán lớp 11: Ôn tập chương 3 (Đại số) đầy đủ nhất

Sau mỗi chương học lý thuyết, để tránh tình trạng đánh rơi kiến thức sau một thời gian không ôn tập, các em cần tích cực giải các bài tập trong sách giáo khoa, sách bài tập để trau dồi kiến thức cùng kỹ năng giải nhanh và chính xác các bài tâp trong chương, chuẩn bị tốt cho kì thi sắp tới. Dưới đây là hướng dẫn giải các bài tập phần ôn tập chương 3 Toán 11, mời các em cùng quý thầy cô tham khảo.

Ôn tập chương 3 (Đại số)

Bài 1 (trang 107 SGK Đại số 11):

Khi nào thì cấp số cộng là dãy số tăng, dãy số giảm?

Hướng dẫn giải chi tiết:

Cấp số cộng (u_n) có công sai d.

+ (u_n) là dãy tăng

⇔ u_{n + 1} > u_n ∀ n ∈ N

⇔ u_{n + 1} – u_n > 0 ∀ n ∈ N

⇔ d > 0

+ (u_n) là dãy giảm

⇔ u_{n + 1} < u_n ∀ n ∈ N

⇔ u_{n + 1} – u_n < 0 ∀ n ∈ N

⇔ d < 0

Kiến thức áp dụng

+ Dãy (u_n) được gọi là dãy tăng ⇔ u_{n + 1} > u_n với mọi n ∈ N*.

+ Dãy (u_n) được gọi là dãy giảm ⇔ u_{n + 1} < u_n với mọi n ∈ N*.

Bài 2 (trang 107 SGK Đại số 11): 

Cho cấp số nhân có u₁ < 0 và công bội q. Hỏi các số hạng khác sẽ mang dấu gì trong các trường hợp sau:

a) q > 0

b) q < 0

Hướng dẫn giải chi tiết:

CSN (u_n) : u_n = u₁.q^{n – 1}, u₁ < 0

a) q > 0 ⇒ q^{n – 1} > 0 ⇒ u₁.q^{n – 1} < 0 (vì u₁ < 0)

⇒ u_n < 0 với mọi n ∈ N*.

Vậy với q > 0 và u₁ < 0 thì các số hạng đều mang dấu âm.

b) q < 0.

+ Nếu n chẵn ⇒ n – 1 lẻ ⇒ q^{n – 1} < 0

⇒ u₁.q^{n – 1} > 0 (vì u₁ < 0).

⇒ u_n > 0.

+ Nếu n lẻ ⇒ n – 1 chẵn ⇒ q^{n – 1} > 0

⇒ u₁.q^{n – 1} < 0 (Vì u₁ < 0).

⇒ u_n < 0.

Vậy nếu q < 0, u₁ < 0 thì các số hạng thứ chẵn dương và các số hạng thứ lẻ âm.

Kiến thức áp dụng

CSN (u_n) có công bội q ; số hạng đầu u₁ thì số hạng thứ n là : u_n = u₁.q^{n – 1}.

Bài 3 (trang 107 SGK Đại số 11): 

Cho hai cấp số cộng có cùng số các số hạng. Tổng các số hạng tương ứng của chúng có lập thành cấp số cộng không? Vì sao? Cho một ví dụ minh họa.

Hướng dẫn giải chi tiết:

Giả sử có hai cấp số cộng (u_n) với công sai d₁ và (v_n) với công sai d₂.

Xét dãy (a_n) với a_n = u_n + v_n

Ta có: a_{n + 1} – a_n = (u_{n + 1} + v_{n + 1}) – (u_n + v_n)

= (u_n + d₁ + v_n + d₂) – (u_n + v_n)

= d₁ + d₂ = const

⇒(a_n) là cấp số cộng với công sai d₁ + d₂.

Ví dụ:

CSC (u_n): 1; 4; 7; 10; 13; 16; 19; …. có công sai d₁ = 3 ;

CSC (v_n): 4 ; 6 ; 8 ; 10 ; 12 ; 14 ; 16 … có công sai d₂ = 2.

⇒ (a_n): 5; 10; 15; 20; 25; 30; 35; … có công sai d = 5.

Kiến thức áp dụng

Để chứng minh dãy (a_n) là CSC ta cần chứng minh a_{n + 1} – a_n = d là một hằng số với mọi n ∈ N*.  

Bài 4 (trang 107 SGK Đại số 11): 

Cho hai cấp số nhân có cùng số các số hạng. Tích các số hạng tương ứng của chúng có lập thành cấp số nhân không? Vì sao? Cho một ví dụ minh họa.

Hướng dẫn giải chi tiết:

Giả sử có hai cấp số nhân (u_n) với công bội q₁ và (v_n) với công bội q₂.

Xét dãy số (a_n) với a_n = u_n.v_n với mọi n ∈ N*.

Ta có:

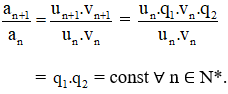
⇒ (a_n) là cấp số nhân với công bội q₁.q₂.

Ví dụ:

+ CSN (u_n) : 2 ; 4 ; 8 ; 16 ; 32 ; 64 ; … có công bội q₁ = 2.

+ CSN (v_n) : -1 ; 1 ; -1 ; 1 ; -1 ; 1 ; … có công bội q₂ = -1.

⇒ CSN (a_n) : -2 ; 4 ; -8 ; 16 ; -32 ; 64 ; … có công bội q = -2.

Kiến thức áp dụng

Để chứng minh (a_n) là một CSN ta cần chứng minh 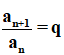 là một hằng số với mọi n ∈ N*.  

Bài 5 (trang 107 SGK Đại số 11): 

Chứng minh với mọi n ∈ N*, ta có:

a) 13ⁿ – 1 chia hết cho 6

b) 3n³ + 15 chia hết cho 9

Hướng dẫn giải chi tiết:

Chứng minh bằng phương pháp quy nạp.

a) Đặt u_n = 13ⁿ – 1

+ Với n = 1 thì u₁ = 13 – 1 = 12 chia hết 6

+ Giả sử: u_k = 13^k – 1 chia hết cho 6.

⇒ u_{k + 1} = 13^{k + 1} – 1

              = 13^k+1 + 13^k – 13^k – 1

              = 13^k(13 – 1) + 13^k – 1

              = 12.13^k + u_k.

Mà 12.13^k ⋮ 6; u_k ⋮ 6.

⇒ u_{k + 1} ⋮ 6.

⇒ u_n ⋮ 6 với mọi n ∈ N.

hay 13ⁿ – 1 ⋮ 6 với mọi n ∈ N.

b) Đặt u_n = 3n³ + 15n

+ Với n = 1 ⇒ u₁ = 18 ⋮ 9.

+ Giả sử với n = k ≥ 1 ta có: u_k = (3k³ + 15k) ⋮ 9

⇒ u_k+1 = 3(k + 1)³ + 15(k + 1 )

              = 3(k³ + 3k² + 3k + 1) + 15k + 15

              = (3k³ + 15k) + 9k² + 9k + 18

              = (3k³ + 15k) + 9(k² + k + 2)

              = u_k + 9(k² + k + 2)

Mà u_k ⋮ 9 và 9(k² + k + 2) ⋮ 9

⇒ u_{k + 1} ⋮ 9.

Vậy u_n = 3n³ + 15n ⋮ 9 ∀n ∈ N*

Kiến thức áp dụng

+ Chứng minh mệnh đề (P) đúng với mọi số tự nhiên n bằng phương pháp quy nạp ta làm như sau:

Bước 1: Kiểm tra mệnh đề đúng với n = 1.

Bước 2: Giả sử mệnh đề đúng với n = k ≥ 1

Cần chứng minh mệnh đề cũng đúng với n = k + 1.

⇒ Mệnh đề đúng với mọi n ∈ N.

Bài 6 (trang 107 SGK Đại số 11): 

Cho dãy số (u_n) biết u₁ = 2, u_{n+ 1} = 2u_n – 1 (với n ≥ 1)

a) Viết năm số hạng đầu của dãy.

b) Chứng minh u_n = 2^n-1 + 1 bằng phương pháp quy nạp.

Hướng dẫn giải chi tiết:

a) 5 số hạng đầu dãy là:

u₁ = 2;

u₂ = 2u₁ – 1 = 3;

u₃ = 2u₂ – 1 = 5;

u₄ = 2u₃ – 1 = 9;

u₅ = 2u₄ – 1 = 17

b) Chứng minh u_n = 2^{n – 1} + 1 (1)

+ Với n = 1 ⇒ u₁ = 2^{1 - 1} + 1 = 2 (đúng).

+ Giả sử (1) đúng với n = k ≥ 1, tức là u_k = 2^k-1 + 1 (1)

Ta chứng minh: u_k+1 = 2^k + 1. Thật vậy, ta có:

⇒ u_k+1 = 2.u_k – 1 = 2(2^k-1 + 1) – 1 = 2.2^{k – 1} + 2 – 1 = 2^k + 1

⇒ (1) cũng đúng với n = k + 1 .

Vậy u_n = 2^{n – 1} + 1 với mọi n ∈ N.

Kiến thức áp dụng

Có ba cách cho một dãy số :

+ Dãy số cho bằng công thức số hạng tổng quát .

Ví dụ : Cho dãy (u_n) với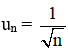 

+ Dãy số cho bằng phương pháp truy hồi .

Ví dụ : Cho dãy (u_n):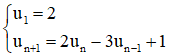 

+ Dãy số cho bằng phương pháp mô tả (ít gặp).

Trong một số bài toán ta có thể chuyển từ dãy số dạng truy hồi về dãy số dạng tổng quát.  

Bài 7 (trang 107 SGK Đại số 11): 

Xét tính tăng, giảm và bị chặn của các dãy số (u_n), biết:

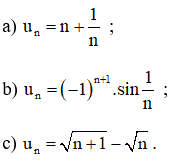
Hướng dẫn giải chi tiết:

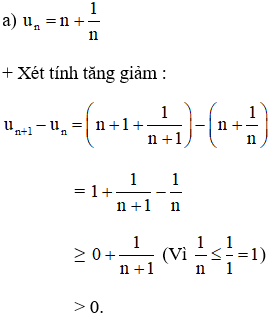
⇒ u_{n + 1} > u_n với mọi n ∈ N

⇒ (u_n) là dãy tăng.

+ Xét tính bị chặn:

(u_n) là dãy tăng

⇒ u₁ = 2 < u₂ < u₃ < …< u_n ∀n ∈ N*

⇒ u_n ≥ 2 ∀n ∈ N*

⇒ (u_n) bị chặn dưới.

(u_n) không bị chặn trên.

⇒ u_n không bị chặn.

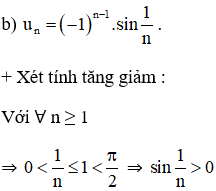
Suy ra: Với n chẵn ⇒ n – 1 lẻ ⇒ (-1)^{n – 1} = -1 ⇒ u_n < 0

Với n lẻ ⇒ n – 1 chẵn ⇒ (-1)^{n – 1} = 1 ⇒ u_n > 0.

⇒ u₁ > u₂ < u₃ > u₄ < u₅ > u₆ …

⇒ (u_n) không tăng không giảm.

+ Xét tính bị chặn :

Với ∀ n ∈ N:

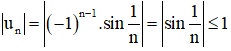
⇒ -1 ≤ u_n ≤ 1.

Vậy (u_n) bị chặn.

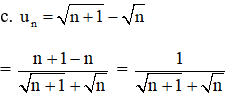
+ Xét tính tăng giảm.

Với mọi n ∈ N ta có:

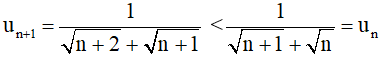
⇒ u_{n + 1} < u_n với mọi n ∈ N.

⇒ (u_n) là dãy số giảm.

+ Xét tính bị chặn.

u_n > 0 với mọi n.

⇒ (u_n) bị chặn dưới.

u_n ≤ u₁ = √2 - 1 với mọi n

⇒ (u_n) bị chặn trên.

⇒ (u_n) bị chặn.

Kiến thức áp dụng

+ Dãy số (u_n) là dãy số tăng ⇔ ∀ n ∈ N ⇔ ∀ n ∈ N.

+ Dãy số (u_n) bị chặn dưới nếu tồn tại số m sao cho u_n > m với ∀ n ∈ N

bị chặn trên nếu tồn tại số M sao cho u_n < M với ∀ n ∈ N.

+ Dãy số (u_n) bị chặn ⇔ (u_n) bị chặn trên và chặn dưới.

►Còn tiếp............

►►►Tải trọn bộ hướng dẫn giải bài tập chi tiết từ bài 1 đến bài 19 SGK Toán lớp 11 trang 107, 108, 109 tại đường link dưới đây.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải bài tập Toán 11: Ôn tập chương 3 (Đại số) đầy đủ nhất file Word, pdf hoàn toàn miễn phí!