Giải Toán Đại 11: Quy tắc tính đạo hàm đầy đủ nhất

Để quá trình tiếp thu kiến thức mới trở nên dễ dàng và đạt hiệu quả nhất, trước khi bắt đầu bài học mới các em cần có sự chuẩn bị nhất định qua việc tổng hợp nội dung kiến thức lý thuyết trọng tâm, sử dụng những kiến thức hiện có thử áp dụng giải các bài toán, trả lời câu hỏi liên quan. Dưới đây chúng tôi đã soạn sẵn Lời giải Toán Đại 11: Quy tắc tính đạo hàm đầy đủ nhất, giúp các em tiết kiệm thời gian. Nội dung chi tiết được chia sẻ dưới đây.

Bài 2: Quy tắc tính đạo hàm

Câu hỏi ứng dụng

Câu hỏi 1 trang 157:

Dùng định nghĩa tính đạo hàm của hàm số y = x³ tại điểm x tùy ý.

Dự đoán đạo hàm của hàm số y = x¹⁰⁰ tại điểm x.

Hướng dẫn giải chi tiết:

- Giả sử Δx là số gia của đối số tại x_o bất kỳ. Ta có:

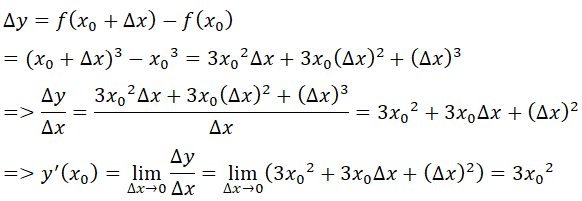
- Dự đoán đạo hàm của y = x¹⁰⁰ tại điểm x là 100x⁹⁹

Câu hỏi 2 trang 158:

Chứng minh khẳng định trong nhận xét trên.

a) Đạo hàm của hàm hằng bằng 0: c’ = 0.

b) Đạo hàm của hàm số y = x bằng 1: x’ = 1.

Hướng dẫn giải chi tiết:

a) Hàm hằng ⇒ Δy = 0

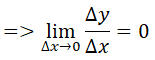
b) theo định lí 1

y = x hay y = x¹ ⇒ y’= (x¹)’= 1. x^1-1 = 1. x^o = 1.1 =1

Câu hỏi 3 trang 158:

Có thể trả lời ngay được không, nếu yêu cầu tính đạo hàm của hàm số f(x) = √x tại x = - 3; x = 4?

Hướng dẫn giải chi tiết:

x = - 3 < 0 hàm số 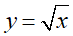 không xác định nên f(x) không có đạo hàm tại x = - 3

x = 4, đạo hàm của f(x) là: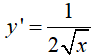 

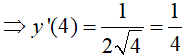
Câu hỏi 4 trang 159:

Áp dụng các công thức trong Định lí 3, hãy tính đạo hàm của các hàm số

y = 5x³ - 2x⁵;

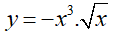
Hướng dẫn giải chi tiết:

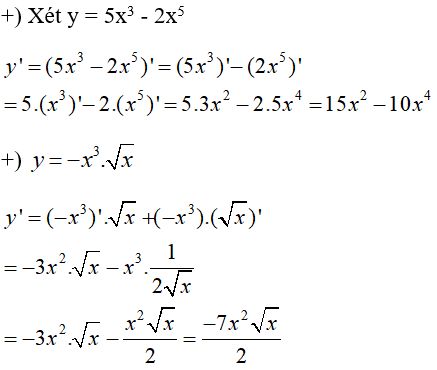
Câu hỏi 5 trang 160:

Hãy chứng minh các công thức trên và lấy ví dụ minh họa.

Hướng dẫn giải chi tiết:

- Nếu k là một hằng số thì (ku)’ = ku’

Thật vậy, ta có: (ku)' = k'u + ku' = 0.u + ku' = ku'

Do đạo hàm của hàm hằng bằng 0

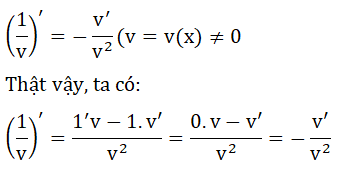
Câu hỏi 6 trang 161:

Hàm số 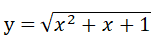 là hàm hợp của hàm số nào ?

Hướng dẫn giải chi tiết:

Hàm số  là hàm hợp của hàm số y = √u với u = x² + x + 1

Bài tập ứng dụng

Bài 1 (trang 162 SGK Đại số 11): 

Bằng định nghĩa, tìm đạo hàm của các hàm số sau :

a. y = 7 + x – x² tại x_o = 1

b. y = x³ – 2x + 1 tại x_o = 2.

Hướng dẫn giải chi tiết:

Cách 1 : Áp dụng công thức

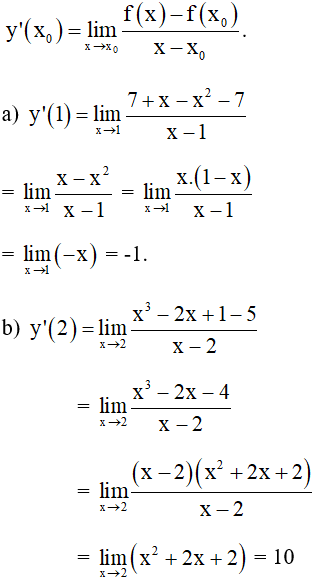
Cách 2 : Áp dụng công thức

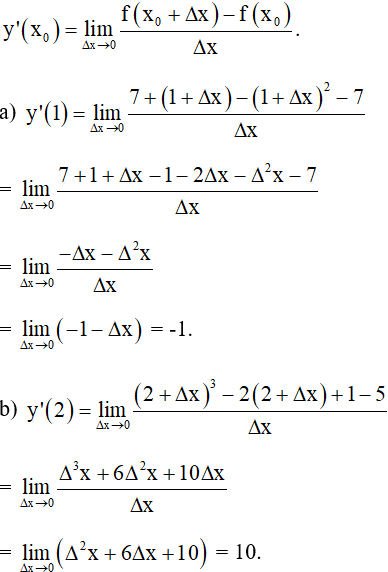
Kiến thức áp dụng

+ Đạo hàm của hàm số y = f(x) tại x = x₀.

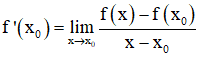
Bài 2 (trang 163 SGK Đại số 11): 

Tìm đạo hàm của các hàm số sau :

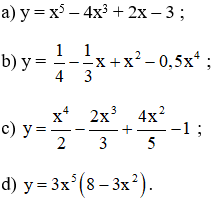
Hướng dẫn giải chi tiết:

a) y’ = (x⁵ – 4x³ + 2x – 3)’

        = (x⁵)’ – (4x³)’ + (2x)’ – (3)’

        = 5x⁴ – 4.3x² + 2

        = 5x⁴ – 12x² + 2.

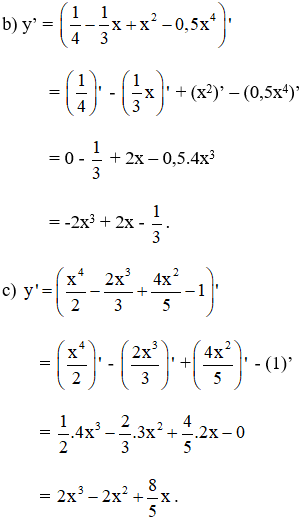
d) Cách 1 : y = 3x⁵ (8 - 3x²)

= 3x⁵.8 – 3x⁵.3x² = 24x⁵ – 9x⁷

⇒ y’ = (24x⁵ – 9x⁷)’

        = (24x⁵)' – (9x⁷)’

        = 24.5x⁴ – 9.7x⁶

        = 120x⁴ – 63x⁶.

Cách 2 : Áp dụng công thức tính đạo hàm của tích :

⇒ y’ = [(3x⁵)’].(8 – 3x²) + 3x⁵.[(8 – 3x²)’]

        = 3.5x⁴(8 – 3x²) + 3x⁵.[(8)’ – (3x²)’]

        = 15x⁴(8 – 3x²) + 3x⁵.(0 – 3.2x)

        = 15x⁴.8 – 15x⁴.3x² + 3x⁵.(-6x)

        = 120x⁴ – 45x⁶ – 18x⁶

        = 120x⁴ – 63x⁶.

Kiến thức áp dụng

+ (x_n)’ = n.x_{n – 1}

+ Với u = u(x) ; v = v(x) là các hàm số có đạo hàm tại x thuộc khoảng xác định ta có :

(u + v)’ = u’ + v’

(u – v)’ = u’ – v’

(k.u)’ = k.u’ (k là hằng số)

(u.v)’ = u’.v + u.v’.

Bài 3 (trang 163 SGK Đại số 11): 

Tìm đạo hàm của các hàm số sau :

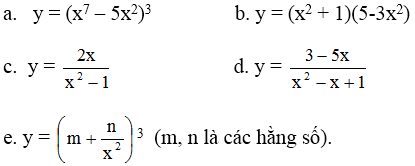
Hướng dẫn giải chi tiết:

a) Cách 1 :

y’ = [(x⁷ - 5x²)³]'

    = [(x⁷)³ – 3.(x⁷)².5x² + 3.x⁷.(5x²)² – (5x²)³]’

    = (x²¹ – 15.x¹⁶ + 75x¹¹ – 125x⁶)’

    = (x²¹)’ – (15x¹⁶)’ + (75x¹¹)’ – (125x⁶)’

    = 21x²⁰ – 15.16x¹⁵ + 75.11x¹⁰ – 125.6x⁵

    = 21x²⁰ – 240x¹⁵ + 825x¹⁰ – 750x⁵.

Cách 2 :

y’ = [(x⁷ - 5x²)³]'

    = 3.(x⁷ – 5x²)².(x⁷ – 5x²)’ (Đạo hàm của hàm hợp với u = x⁷ – 5x² ; y = u³)

    = 3.(x⁷ – 5x²)².[ (x⁷)’ – (5x²)’]

    = 3.(x⁷ – 5x²)²(7x⁶ – 5.2x)

    = 3.(x⁷ – 5x²)²(7x⁶ – 10x)

b) y’ = [(x² + 1)(5 – 3x²)]’

    = (x² + 1)’.(5 – 3x²) + (x² + 1)(5 – 3x²)’ (Đạo hàm của tích)

    = [(x²)’ + (1)’](5 – 3x²) + (x² + 1)[(5)’ – (3x²)’]

    = (2x + 0)(5 – 3x²) + (x² + 1)(0 – 3.2x)

    = 2x.(5 – 3x²) + (x² + 1).(-6x)

    = 2x.5 – 2x.3x² + x²(-6x) + 1(-6x)

    = 10x – 6x³ – 6x³ – 6x

    = -12x³ + 4x.

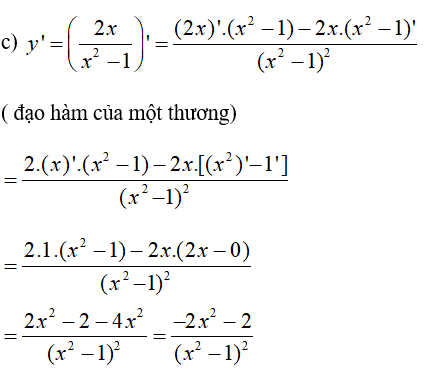
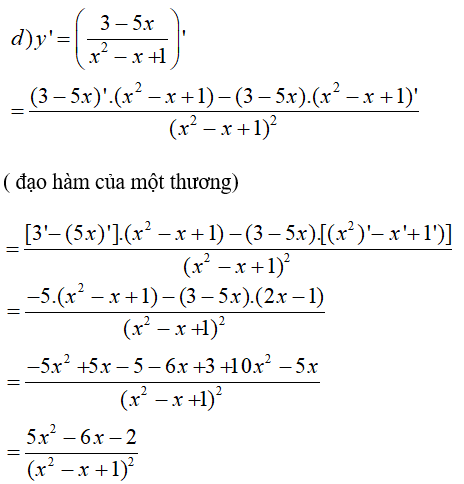
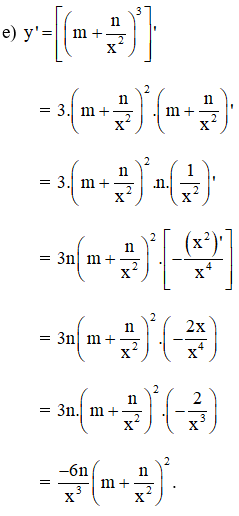
Kiến thức áp dụng

+ (xⁿ)’ = n.x^{n – 1}

+ Với u = u(x) ; v = v(x) là các hàm số có đạo hàm tại x thuộc khoảng xác định ta có :

(u + v)’ = u’ + v’

(u – v)’ = u’ – v’

(u.v)’ = u’.v + u.v’.

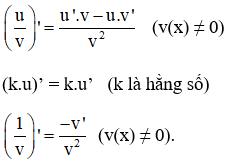
+ Đạo hàm của hàm hợp:

Hàm số y = f(u) với u = g(x) thì hàm số y = f(g(x)) có đạo hàm:

y’ = f’(u).g’(x).

Bài 4 (trang 163 SGK Đại số 11): 

Tính đạo hàm của các hàm số sau:

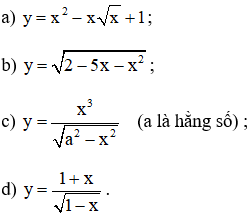
Hướng dẫn giải chi tiết:

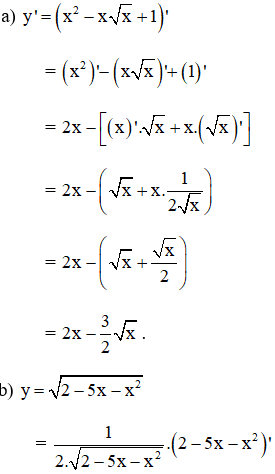
(Đạo hàm của hàm hợp với u = 2 – 5x – x² và y = √u)

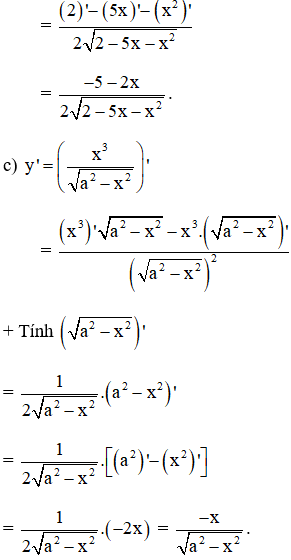
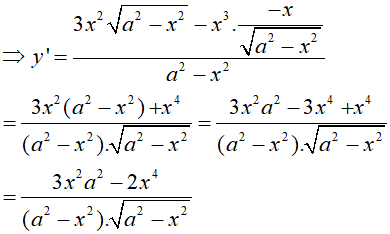
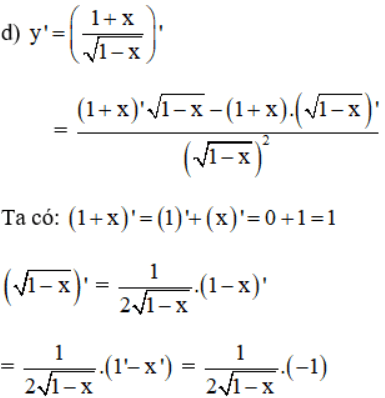
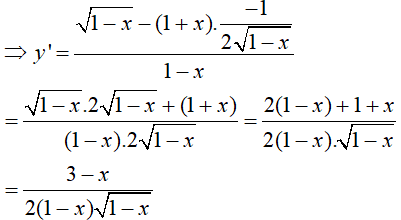
Kiến thức áp dụng

+ (xⁿ)’ = n.x^{n – 1}

+ Với u = u(x) ; v = v(x) là các hàm số có đạo hàm tại x thuộc khoảng xác định ta có :

(u + v)’ = u’ + v’

(u – v)’ = u’ – v’

(u.v)’ = u’.v + u.v’.

+ Đạo hàm của hàm hợp:

Hàm số y = f(u) với u = g(x) thì hàm số y = f(g(x)) có đạo hàm:

y’ = f’(u).g’(x).

Bài 5 (trang 163 SGK Đại số 11): 

Cho y=x³-3x²+2. Tìm x để:

a. y^' > 0

b. y^' < 3

Hướng dẫn giải chi tiết:

y = x³ – 3x² + 2.

⇒ y’ = (x³ – 3x² + 2)’

      = (x³)’ – (3x²)’ + (2)’

      = 3x² – 3.2x + 0

      = 3x² – 6x.

a) y’ > 0

⇔ 3x² – 6x > 0

⇔ 3x(x – 2) > 0

⇔ x < 0 hoặc x > 2.

b) y’ < 3

⇔ 3x² – 6x < 3

⇔ 3x² – 6x – 3 < 0

⇔ 1- √2 < x < 1 + √2.

Lý thuyết trọng tâm

I. Đạo hàm của một số hàm số thường gặp

Định lí 1

    Hàm số y = xⁿ (n ∈ N, n > 1) có đạo hàm tại mọi x ∈ R và (xⁿ)’ = nx^{n – 1}

Định lí 2

    Hàm số y = √x có đạo hàm tại mọi x dương và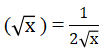 

II. Đạo hàm của tổng, hiệu, tích, thương

1. Định lí

Định lí 3

Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có

    (u + v)’ = u’ + v’

    (u – v)’ = u’ – v’

    (uv)’ = u’v – v’u

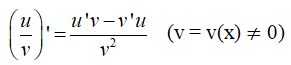
2. Hệ quả

Hệ quả 1

    Nếu k là một hằng số thì (ku)’ = ku’.

Hệ quả 2

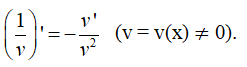
III. Đạo hàm của hàm hợp

Định lí 4

    Nếu hàm số u = g(x) có đạo hàm tại x là u'_x và hàm số y = f(u) có đạo hàm tại u là y'_u thì hàm hợp y = f(g(x)) có đạo hàm tại x là y'_x = y'_u.u'_x .

File tải hướng dẫn giải Toán Đại 11: Quy tắc tính đạo hàm:

Hy vọng tài liệu sẽ hữu ích cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác.

►Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích hỗ trợ ôn luyện thi môn toán như đề kiểm tra học kì, 1 tiết, 15 phút trên lớp, hướng dẫn giải sách giáo khoa, sách bài tập được cập nhật liên tục tại chuyên trang của chúng tôi.