Các dạng bài tập tìm cực trị của hàm số hay nhất

Hàm số có cực trị khi nào? Cùng chúng tôi tóm tắt lại lý thuyết về cực trị của hàm số bao gồm các nội dung trọng tâm dưới đây để dễ dàng "công phá" các bài toán cực trị trong thời gian ngắn nhất.

Định nghĩa cực trị hàm số

- Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b) (a có thể là −∞, b có thể là +∞) và điểm x0 ∈ (a;b).

+ Nếu tồn tại số h>0 sao cho f(x)<f(x0) với mọi x ∈ (x0 - h; x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực đại tại x0.

+ Nếu tồn tại số h>0 sao cho f(x)>f(x0) với mọi x ∈ (x0 - h; x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.

Chú ý:

- Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x0 thì:

+ x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số.

+ f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, ký hiệu: fCĐ (fCT)

+ M(x0;f(x0)) gọi là điểm cực đại (điểm cực tiểu) của đồ thị.

- Các điểm cực đại và cực tiểu gọi chung là điểm cực trị

+ Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và gọi chung là cực trị của hàm số.

- Nếu hàm số y = f(x) có đạo hàm trên khoảng (a;b) và đạt cực đại hoặc cực tiểu tại x0 thì f'(x0) = 0.

Điều kiện đủ để hàm số có cực trị

- Khi f'(x) đổi dấu từ dương sang âm qua x = c thì x = c được gọi là điểm cực đại của hàm số.

- Khi f'(x) đổi dấu từ âm sang dương qua x = c thì x = c được gọi là điểm cực tiểu của hàm số.

Cách tìm cực trị của hàm số

Các em học sinh cần ghi nhớ hai cách tính cực trị hàm số dưới đây:

Quy tắc tìm cực trị 1:

- Bước 1: Tìm tập xác định

- Bươc 2: Tính f'(x). Tìm các điểm tại đó f'(x) = 0 hoặc f'(x) không xác định.

- Bước 3: Lập bảng biến thiên

- Bước 4: Từ bảng biến thiên suy ra cực trị:

+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.

+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.

Quy tắc tìm cực trị 2:

- Bước 1: Tìm tập xác định

- Bươc 2: Tính f'(x). Giải phương trình f'(x) = 0 tìm các nghiệm xi (i=1,2,...)

- Bước 3: Tính f''(x) và tính các giá trị f''(xi)

- Bước 4: Dựa vào dấu của f''(xi) suy ra tính chất cực trị tại xi.

+ Tại các điểm xi mà f''(xi) > 0 thì đó là điểm cực tiểu của hàm số.

+ Tại các điểm xi mà f''(xi) < 0 thì đó là điểm cực đại của hàm số.

Các dạng bài tập trắc nghiệm tìm cực trị hàm số hay nhất

Hàm số có cực trị hay không có cực trị khi nào? Mời các bạn tham khảo ngay các câu trắc nghiệm thuộc 9 dạng bài toán cực trị của hàm số có đáp án và lời giải chi tiết được chọn lọc từ các đề thi thử, đề tham khảo và đề minh họa THPT Quốc gia môn Toán của Bộ Giáo dục và Đào tạo trong các năm gần đây.

Trong mỗi dạng bài, chúng tôi xin đưa ra một vài câu hỏi ví dụ, các bạn sẽ xem 132 câu hỏi kèm đáp án trong file PDF hỗ trợ tải miễn phí tại đây:

Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó

Câu 1. Cho hàm số y = f(x) có bảng biến thiên như sau:

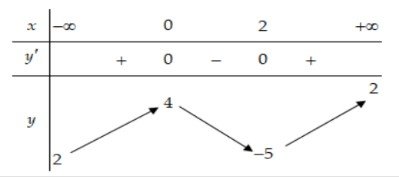
Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực tiểu tại x = -5

B. Hàm số có bốn điểm cực trị

C. Hàm số đạt cực tiểu tại x- 2

D. Hàm số không có cực đại

Câu 2. Cho hàm số y = f(x) có bảng biến thiên như sau:

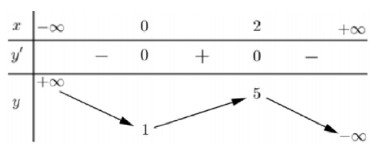
Giá trị cực đại của hàm số đã cho bằng A. 5    B. 2    C. 0    D. 1

Dạng 2. Tìm cực trị của hàm số khi biết y, y'

Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0

Dạng 4. Tìm m để hàm số có n cực trị

Dạng 5. Đường thẳng đi qua 2 điểm cực trị

Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước

Dạng 7. Tam giác cực trị

Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối

Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f'(x)

Trên đây là tổng hợp lý thuyết và các dạng bài tập trắc nghiệm tìm điểm cực trị của hàm số thường xuất hiện trong các đề thi, đề kiểm tra môn Toán có đáp án và hướng dẫn giải chi tiết. Các bạn hãy chia sẻ nội dung hữu ích này cho bạn bè và người thân cùng tham khảo nhé.