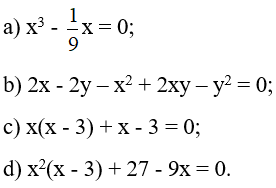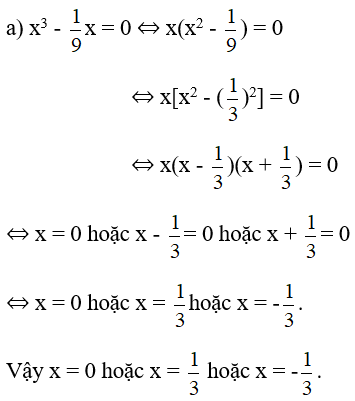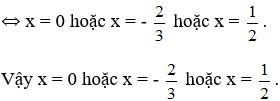Giải Toán lớp 8 VNEN Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử và phối hợp nhiều phương pháp

Hướng dẫn giải bài tập Toán lớp 8 VNEN Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử và phối hợp nhiều phương pháp chi tiết, dễ hiểu được biên soạn bởi đội ngũ chuyên gia giàu kinh nghiệm chia sẻ. Hy vọng đây sẽ là tài liệu hữu ích hỗ trợ học sinh trong quá trình học tập. Mời các em tham khảo tại đây.

Giải Toán 8 VNEN Bài 7: Hoạt động khởi động và hình thành kiến thức.

Câu 1 (Trang 20 Toán 8 VNEN Tập 1)

a) Phân tích đa thức x² - 2x + xy - 2y thành nhân tử.

Lời giải:

Cách 1: x² - 2x + xy - 2y = (x² - 2x) + (xy - 2y) = x(x - 2) + y(x - 2) = (x - 2)(x + y).

Cách 2: x² - 2x + xy - 2y = (x² + xy) - (2x + 2y) = x(x + y) - 2(x + y) = (x + y)(x - 2).

b) Phân tích các đa thức sau thành nhân tử:

x³ - 2x² - x + 2;             x² + 6x – y² + 9.

Lời giải:

x³ - 2x² - x + 2 = x²( x - 2) - (x - 2) = (x - 2)(x² - 1);

x² + 6x – y² + 9 = (x² + 6x + 9) – y² = (x + 3)² – y² = (x + 3 - y)(x + 3 + y).

Câu 2 (Trang 20 Toán 8 VNEN Tập 1)

a) Thực hiện các yêu cầu sau:

- Viết tiếp vào chỗ trống theo mẫu để chỉ rõ đã sử dụng những phương pháp nào để phân tích đa thức thành nhân tử:

x² + 3x - 2xy - 3y + y²

= (x² - 2xy + y²) + (3x - 3y) ( Phương pháp nhóm hạng tử)

= (x - y)² + 3(x - y) (Phương pháp ................. và phương pháp ....................)

= (x - y)(x - y + 3) (Phương pháp ..................)

Lời giải:

x² + 3x - 2xy - 3y + y²

= (x² - 2xy + y²) + (3x - 3y) ( Phương pháp nhóm hạng tử)

= (x - y)² + 3(x - y) (Phương pháp sử dụng hằng đẳng thức và phương pháp đặt nhân tử chung)

= (x - y)(x - y + 3) (Phương pháp đặt nhân tử chung).

- Phân tích đa thức sau thành nhân tử: x² - 2x - 3.

Lời giải:

x² - 2x - 3 = x² - 3x + x - 3 = x(x - 3) + (x - 3) = (x - 3)(x + 1).

b) Phân tích đa thức 2x³y - 2xy³ - 4xy² - 2xy thành nhân tử.

Lời giải:

2x³y - 2xy³ - 4xy² - 2xy

= 2xy(x² – y² - 2y - 1)

= 2xy[x² - (y² + 2y + 1)]

= 2xy[x² - (y + 1)²]

= 2xy(x - y -1)(x + y + 1).

Giải Toán VNEN lớp 8 Bài 7: Hoạt động luyện tập

Câu 1 (Trang 21 Toán 8 VNEN Tập 1)

a) 2x² - 2xy - 5x + 5y;

b) 8x³ + 4xy - 2ax - ay;

c) x³ - 4x² + 4x;

d) 2xy – x² – y² + 16;

e) x² – y² - 2yz – z²;

g) 3a² - 6ab + 3b² - 12c².

Lời giải:

a) 2x² - 2xy - 5x + 5y = 2x(x - y) - 5(x - y) = (x - y)(2x - 5);

b) 8x² + 4xy - 2ax - ay = 4x(2x + y) - a(2x + y) = (2x + y)(4x - a);

c) x³ - 4x² + 4x = x(x² - 4x + 4) = x(x - 2)²;

d) 2xy – x² – y² + 16 = 16 - (x² - 2xy + y²) = 42 - (x - y)² = (4 - x + y)(4 + x - y);

e) x² – y² - 2yz – z² = x² - (y² + 2yz + z²) = x² - (y + z)² = (x - y - z)(x + y + z);

g) 3a² - 6ab + 3b² - 12c² = 3(a² - 2ab + b² - 4c²) = 3[(a - b)² - (4c)²] = 3(a - b - 4 c)(a - b + 4c).

Câu 2 (Trang 21 Toán 8 VNEN Tập 1)

Tính nhanh:

a) 37,5.8,5 - 7,5.3,4 - 6,6.7,5 + 1,5.37,5;

b) 35² + 40² – 25² + 80.35.

Lời giải:

a) 37,5.8,5 - 7,5.3,4 - 6,6.7,5 + 1,5.37,5

= (37,5.8,5 + 1,5.37,5) - (7,5.3,4 + 6,6.7,5)

= 37,5(8,5 + 1,5) - 7,5(3,4 + 6,6)

= 37,5.10 - 7,5.10 = 375 - 75 = 300;

b) 35² + 40² – 25² + 80.35 = (35² + 2.40.35 + 40²) – 25² = (35 + 40)² – 25²

= (75 - 25)(75 + 25) = 50.100 = 5000.

Câu 3 (Trang 21 Toán 8 VNEN Tập 1)

Tìm x, biết:

Lời giải:

b) 2x - 2y – x² + 2xy – y² = 0

⇔ 2(x - y) - (x - y)² = 0

⇔ (x - y)(2 - x + y) = 0

⇔ x - y = 0 hoặc 2 - x + y = 0

⇔ x = y hoặc x = 2 + y.

Vậy x = y hoặc x = 2 + y.

c) x(x - 3) + x - 3 = 0

⇔ (x - 3)(x + 1) = 0

⇔ x - 3 = 0 hoặc x + 1 = 0

⇔ x = 3 hoặc x = -1.

Vậy x = 3 hoặc x = -1.

d) x²(x - 3) + 27 - 9x = 0

⇔ x²(x - 3) - 9(x - 3) = 0

⇔ (x - 3)(x² - 9) = 0

⇔ (x - 3)(x - 3)(x + 3) = 0

⇔ x - 3 = 0 hoặc x + 3 = 0

⇔ x = 3 hoặc x = -3.

Vậy x = 3 hoặc x = -3.

Câu 4 (Trang 22 Toán 8 VNEN Tập 1)

Phân tích các đa thức sau thành nhân tử:

a) x² - 4x + 3;

b) x² + x - 6;

c) x² - 5x + 6;

d) x⁴ + 4.

Lời giải:

a) x² - 4x + 3 = x² - x - 3x + 3 = x( x - 1) - 3(x - 1) = (x - 3)(x - 1);

b) x² + x - 6 = x² - 2x + 3x - 6 = x(x - 2) + 3(x - 2) = (x - 2)(x + 3);

c) x² - 5x + 6 = x² - 2x - 3x + 6 = x(x - 2) - 3(x - 2) = (x - 2)(x - 3);

d) x⁴ + 4 = x⁴ + 4x² - 4x² + 4 = x⁴ + 4x² + 4 - 4x² = (x⁴ + 4x² + 4) - 4x²

= (x² + 2)² - (2x)² = (x² + 2 + 2x)(x² + 2 - 2x).

Giải SGK Toán 8 VNEN Bài 7: Hoạt động vận dụng

Câu 1 (Trang 22 Toán 8 VNEN Tập 1)

Chứng minh rằng: (3n + 4)² - 16 chia hết cho 3 với mọi số nguyên n.

Lời giải:

Có: (3n + 4)² - 16 = (3n + 4)² – 4² = (3n + 4 - 4)(3n + 4 + 4) = 3n(3n + 8) luôn chia hết cho 3 với mọi số nguyên n.

Vậy (3n + 4)² - 16 luôn chia hết cho 3 với mọi số nguyên n.

Câu 2 (Trang 22 Toán 8 VNEN Tập 1)

Tính nhanh giá trị của biểu thức sau:

M = a³ – a²b – ab² + b³ với a = 5,75; b = 4,25.

Lời giải:

M = a³ – a²b – ab² + b³

= (a³ + b³) - (a²b + ab²)

= (a + b)(a² - ab + b²) - ab(a + b)

= (a + b)(a² - ab + b² - ab)

= (a + b)(a² - 2ab + b²)

= (a + b)(a - b)².

Thay a = 5,75 và b = 4,25 vào M, ta được:

M = (5,75 + 4,25)(5,75 - 4,25)² = 22,5.

Câu 3 (Trang 5 Toán 22 VNEN Tập 1)

Tìm x, biết:

a) x² + x = 6;

b) 6x³ + x² = 2x.

Lời giải:

a) x² + x = 6

⇔ x² + x - 6 = 0

⇔ x+2 - 2x + 3x - 6 = 0

⇔ x(x - 2) + 3(x - 2) = 0

⇔ (x - 2)(x + 3) = 0

⇔ x = 2 hoặc x = -3.

Vậy x = 2 hoặc x = -3.

b) 6x³ + x² = 2x

⇔ 6x³ + x² - 2x = 0

⇔ x(6x² + x - 2) = 0

⇔ x(6x² - 3x + 4x - 2) = 0

⇔ x[3x(2x - 1) + 2(2x - 1)] = 0

⇔ x(3x + 2)(2x - 1) = 0

Giải VNEN Toán 8 Bài 7: Hoạt động tìm tòi mở rộng

Đọc sách

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán lớp 8 VNEN Tập 1 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử và phối hợp nhiều phương pháp file PDF hoàn toàn miễn phí.