Soạn Toán Lớp 6 Bài 18: Bội chung nhỏ nhất

Trước khi bắt đầu tiếp thu nội dung kiến thức mới, để quá trình diễn ra dễ dàng và đạt hiệu quả cao các em học sinh cần chuẩn bị trước bài mới thông qua nghiên cứu nội dung kiến thức lý thuyết, ứng dụng giải các bài tập và trả lời các câu hỏi cuối bài. Tuy nhiên không phải ai cũng có thể hoàn thành tốt và đầy đủ những gì cần chuẩn bị. Thấu hiểu điều đó, chúng tôi xin chia sẻ bài Soạn Toán Lớp 6 Bài 18: Bội chung nhỏ nhất đầy đủ từ đội ngũ chuyên gia giàu kinh nghiệm. Hy vọng sẽ là tài liệu hữu ích dành cho các em và quý thầy cô tham khảo.

Bài 18: Bội chung nhỏ nhất

Bài tập:

Câu hỏi trang 58:

Tìm BCNN(8, 12); BCNN(5, 7, 8); BCNN(12, 16, 48).

Lời giải

* Tìm BCNN(8 ; 12) :

+ Phân tích thành thừa số nguyên tố :

8 = 2³

12 = 2².3.

+ Các thừa số nguyên tố chung và riêng là : 2 ; 3.

⇒ BCNN(8 ; 12) = 2³.3 = 24.

* Tìm BCNN(5 ; 7 ; 8)

+ Phân tích thành thừa số nguyên tố :

5 = 5

7 = 7

8 = 2³.

+ Các thừa số nguyên tố chung và riêng : 2 ; 5 ; 7.

⇒ BCNN(5 ; 7 ; 8) = 2³.5.7 = 280.

* Tìm BCNN(12 ; 16 ; 48).

+ Phân tích thành thừa số nguyên tố :

12 = 2².3

16 = 2⁴

48 = 2⁴.3.

+ Các thừa số nguyên tố chung và riêng : 2 ; 3.

⇒ BCNN(12; 16; 48) = 2⁴.3 = 48.

Bài 149 (trang 59 sgk Toán 6 Tập 1):

Tìm BCNN của:

a) 60 và 280 ;     b) 84 và 108 ;     c) 13 và 15

Lời giải:

a) – Phân tích ra thừa số nguyên tố:

60 = 2².3.5; 280 = 2³.5.7

– Chọn ra các thừa số nguyên tố chung và riêng: 2; 3; 5; 7.

– Lập tích: mỗi thừa số lấy với sỗ mũ lớn nhất: số mũ lớn nhất của 2 là 3; số mũ lớn nhất của 3; 5; 7 là 1.

BCNN(60; 280) = 2³.3.5.7 = 840.

b) 84 = 2².3.7; 108 = 2².3³

⇒ BCNN(84; 108) = 2².3³.7 = 756

c) 13 = 13; 15 = 3.5

⇒ BCNN(13; 15) = 3.5.13 = 195.

Kiến thức áp dụng

Muốn tìm BCNN của hai hay nhiều số ta làm như sau:

+ Phân tích các số ra thừa số nguyên tố.

+ Chọn ra các thừa số nguyên tố chung và riêng.

+ Lập tích các thừa số đã chọn; mỗi thừa số lấy số mũ lớn nhất của nó. Tích đó chính là BCNN cần tìm.

Bài 150 (trang 59 sgk Toán 6 Tập 1):

Tìm BCNN của:

a) 10, 12, 15 ;     b) 8, 9, 11 ;     c) 24, 40, 168

Lời giải:

a) 10 = 2.5; 12 = 2².3; 15 = 3.5

⇒ BCNN(10, 12, 15) = 2².3.5 = 60.

b) 8 = 2³ ; 9 = 3²; 11 = 11

⇒ BCNN(8; 9; 11) = 2³.3².11 = 792.

c) 24 = 2³.3; 40 = 2³.5; 168 = 2³.3.7

⇒ BCNN(24, 40, 168) = 2³.3.5.7 = 840.

Kiến thức áp dụng

Muốn tìm BCNN của hai hay nhiều số ta làm như sau:

+ Phân tích các số ra thừa số nguyên tố.

+ Chọn ra các thừa số nguyên tố chung và riêng.

+ Lập tích các thừa số đã chọn; mỗi thừa số lấy số mũ lớn nhất của nó. Tích đó chính là BCNN cần tìm.

Bài 151 (trang 59 sgk Toán 6 Tập 1):

Hãy tính nhẩm BCNN của các số sau bằng cách nhân số lớn nhất lần lượt với 1, 2, 3, ... cho đến khi được kết quả là một số chia hết cho các số còn lại:

a) 30 và 150 ;     b) 40, 28, 140 ;     c) 100, 120, 200

Lời giải:

a) Ta có: 150 ⋮ 30

⇒ BCNN(150, 30) = 150

b) Ta có : 140 ⋮̸ 40.

140. 2 = 280 ⋮ 40 và 280 ⋮ 28

Vậy BCNN (40, 28, 140) = 280.

c) 200 ⋮̸ 120.

200.2 = 400 ⋮̸ 120.

200.3 = 600 ⋮ 120 và 600 ⋮ 100.

Vậy BCNN(100, 120, 200) = 600.

Bài 152 (trang 59 sgk Toán 6 Tập 1):

Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a chia hết cho 15 và a chia hết cho 18.

Lời giải:

Ta có a ⋮ 15 và a ⋮18 ⇒ a ∈ BC(15, 18).

a là số nhỏ nhất nên a = BCNN(15 ; 18).

Mà 15 = 3.5; 18 = 2.3².

⇒ BCNN(15; 18) = 2.3².5 = 90.

Vậy a = 90.

Kiến thức áp dụng

Muốn tìm BCNN của hai hay nhiều số ta làm như sau:

+ Phân tích các số ra thừa số nguyên tố.

+ Chọn ra các thừa số nguyên tố chung và riêng.

+ Lập tích các thừa số đã chọn; mỗi thừa số lấy số mũ lớn nhất của nó. Tích đó chính là BCNN cần tìm. 

Bài 153 (trang 59 sgk Toán 6 Tập 1):

Tìm các bội chung nhỏ hơn 500 của 30 và 45.

Lời giải:

Có 30 = 2.3.5; 45 = 3².5

⇒ BCNN(30,45) = 2.3².5 = 90

⇒ BC(30; 45) = B(90) = {0; 90; 180; 270; 360; 450; 540; 630; …}

Vậy các bội chung nhỏ hơn 500 của 30 và 45 là: 0; 90; 180; 270; 360; 450.

Kiến thức áp dụng

Bội chung của hai hay nhiều số là bội của BCNN của các số đó.

Bài 154 (trang 59 sgk Toán 6 Tập 1):

Học sinh lớp 6C khi xếp hàng 2, hàng 3, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng từ 35 đến 60. Tính số học sinh lớp 6C.

Lời giải:

Gọi số học sinh lớp 6C là a.

Học sinh xếp hàng 2, hàng 3, hàng 4, hàng 8 đều vừa đủ nên a là bội của 2, 3, 4, 8.

Hay a ∈ BC(2; 3; 4; 8).

+ Tìm BC(2; 3; 4; 8):

Ta có: 2 = 2; 3 = 3; 4 = 2²; 8 = 2³

⇒ BCNN(2 ; 3 ; 4 ; 8) = 2³. 3 = 24.

⇒ BC(2; 3; 4; 8) = B(24) = {0; 24; 48; 72; …}.

Vì số học sinh trong khoảng từ 35 đến 60 nên a = 48.

Vậy lớp 6C có 48 học sinh.

Bài 155 (trang 60 sgk Toán 6 Tập 1):

Cho bảng:

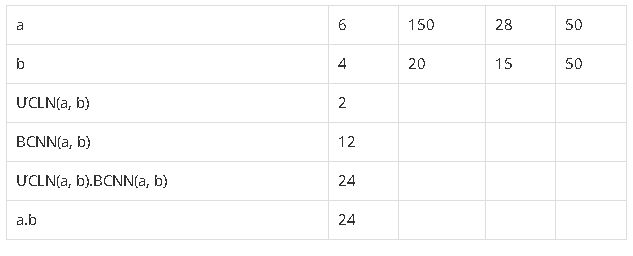
a) Điền vào các ô trống của bảng.

b) So sánh tích ƯCLN(a, b).BCNN(a, b) với tích a.b

Lời giải:

a)

– Ở cột thứ hai:

a = 150 = 2.3.5²; b = 20 = 2².5

⇒ ƯCLN(a; b) = 2.5 = 10; BCNN(a; b) = 2².3.5² = 300.

ƯCLN(a, b) . BCNN(a, b) = 10.300 = 3000.

a.b = 150.20 = 3000.

– Ở cột thứ ba:

a = 28 = 2².7; b = 15 = 3.5

⇒ ƯCLN(a; b) = 1; BCNN(a; b) = 2².3.5.7 = 420.

ƯCLN(a, b) . BCNN(a, b) = 1.420 = 420.

a.b = 28.15 = 420.

– Ở cột thứ tư:

a = b = 50.

⇒ ƯCLN(a; b) = 50; BCNN(a; b) = 50.

ƯCLN(a, b) . BCNN(a, b) = 50.50 = 2500.

a . b = 2500.

Ta có bảng sau:

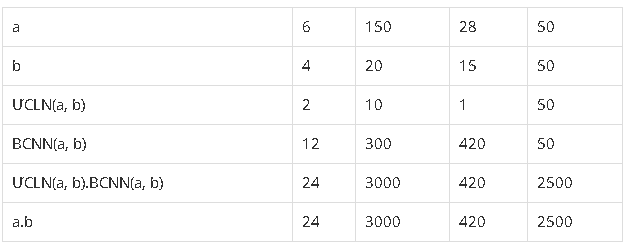
Bài 156 (trang 60 sgk Toán 6 Tập 1): Tìm số tự nhiên x biết rằng:

x ⋮ 12, x ⋮ 21, x ⋮ 28 và 150 < x < 300

Lời giải:

x ⋮ 12; x ⋮ 21; x ⋮ 28 nên x ∈ BC(12; 21; 28).

12 = 2².3; 21 = 3.7; 28 = 2².7

⇒ BCNN(12; 21; 28) = 2².3.7 = 84.

⇒ x ∈ BC(12; 21; 28) = B(84) = {0; 84; 168; 252; 336; 420; …}.

Vì 150 < x < 300 nên x = 168 hoặc x = 252.

Kiến thức áp dụng

+ x ⋮ a; x ⋮ b; x ⋮ c; x ⋮ d; … thì x ∈ BC(a; b; c; d; …).

+ Bội chung của hai hay nhiều số là bội của BCNN của các số đó.

Bài 157 (trang 60 sgk Toán 6 Tập 1):

Hai bạn An và Bách cùng học một trường nhưng ở hai lớp khác nhau. An cứ 10 ngày lại trực nhật, Bách cứ 12 ngày lại trực nhật. Lần đầu cả hai bạn cùng trực nhật vào một ngày. Hỏi sau ít nhất bao nhiêu ngày thì hai bạn lại cùng trực nhật?

Lời giải:

Giả sử sau x ngày An và Bách lại cùng trực nhật.

An cứ 10 ngày trực nhật một lần nên x là bội của 10.

Bách cứ 12 ngày trực nhật một lần nên x là bội của 12.

Suy ra x ∈ BC(10; 12).

Mà x ít nhất nên x = BCNN(10; 12).

10 = 2.5; 12 = 2². 3

⇒ x = BCNN(10; 12) = 2².3.5 = 60.

Vậy sau 60 ngày An và Bách lại cùng trực nhật.

Bài 158 (trang 60 sgk Toán 6 Tập 1):

Hai đội công nhân nhận trồng một số cây như nhau. Mỗi công nhân đội I phải trồng 8 cây, mỗi công nhân đội II phải trồng 9 cây. Tính số cây mỗi đội phải trồng biết rằng số cây đó trong khoảng từ 100 đến 200.

Lời giải:

Giả sử mỗi đội phải trồng x cây.

Mỗi công nhân đội I trồng 8 cây nên x ⋮ 8.

Mỗi công nhân đội II trồng 9 cây nên x ⋮ 9.

Do đó x ∈ BC(8; 9).

Mà BCNN(8; 9) = 72

nên x ∈ BC(8; 9) = B(72) = {0; 72; 144; 216; 288; …}.

Vì 100 < x < 200 nên x = 144.

Vậy mỗi đội phải trồng 144 cây.

Lý thuyết:

Định nghĩa: Bội chung nhỏ nhất (BCNN) của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Ví dụ:

B(4) = {0; 4; 8; 12; 16; 20; 24; ...}

B(6) = {0; 6; 12; 18; 24; ...}

⇒ BC(4; 6) = {0; 12; 24; ...}

⇒ BCNN(4; 6) = 12

Chú ý: Mọi số tự nhiên đều là bội của 1. Do đó: Với mọi số tự nhiên a và b ( khác 0) ta có:

BCNN(a; 1) = a; BCNN(a,b,1) = BCNN(a,b)

Ví dụ:

BCNN(6;1) = 6

BCNN(6;8;1) = BCNN(6;8)

Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố

Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:

+ Phân tích mỗi số ra thừa số nguyên tố.

+ Chọn ra các thừa tố nguyên tố chung và riêng.

+ Lập tích các thừa số đã chọn, mỗi thừa số lấy số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

Ví dụ: Tìm BCNN(8;12)

Ta có:

8 = 2³

12 = 2³

Chọn ra các thừa số chung và riêng, đó là 2 và 3. Số mũ lớn nhất của 2 là 3, số mũ lớn nhất của 3 là 1. Khi đó:

BCNN(8; 12) = 2³.3 = 24

Chú ý:

- Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó

Ví dụ: BCNN(3; 5; 7) = 3.5.7 = 105

- Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.

Ví dụ: BCNN(12;16;48) = 48

Cách tìm bội chung thông qua tìm BCNN

Để tìm bội chung của các số đã cho, ta có thể tìm các bội của BCNN của các số đó

Ví dụ: Tìm bội chung của 8 và 12

Ta đã chỉ ra ở VD trên: BCNN(8; 12) = 24

⇒ BC(8; 12) = B(24) = {0; 24; 48; 72;...}

File tải miễn phí bài soạn Toán Lớp 6 Bài 18: Bội chung nhỏ nhất đầy đủ:

Hy vọng tài liệu sẽ hữu ích cho các em học sinh và quý thầy cô tham khảo.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích hỗ trợ ôn luyện thi môn toán như đề kiểm tra, hướng dẫn giải sách giáo khoa, vở bài tập được cập nhật liên tục tại chuyên trang của chúng tôi.