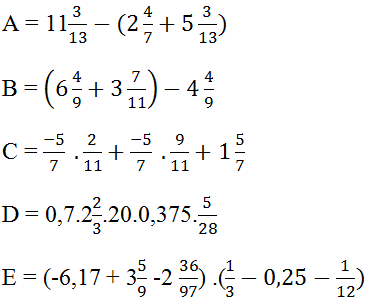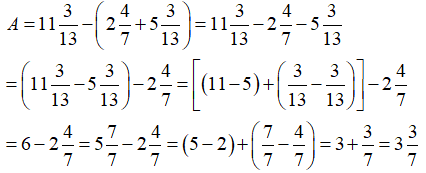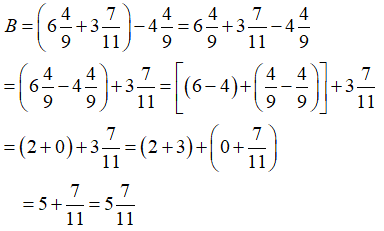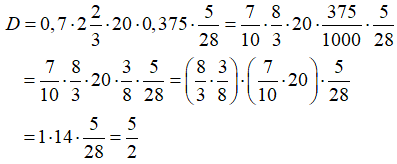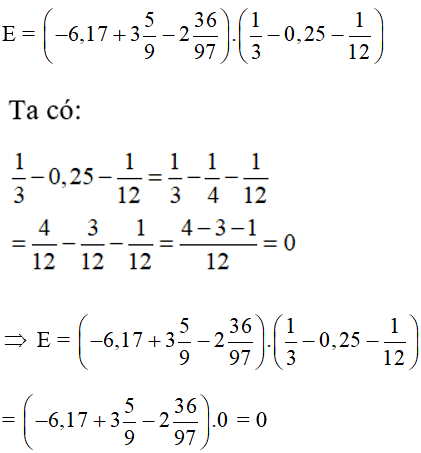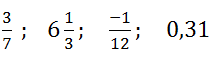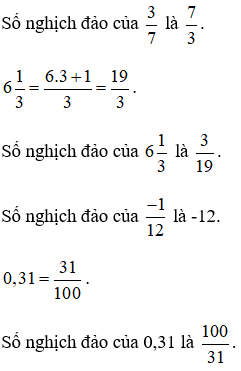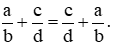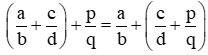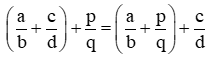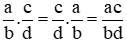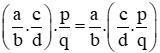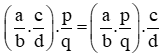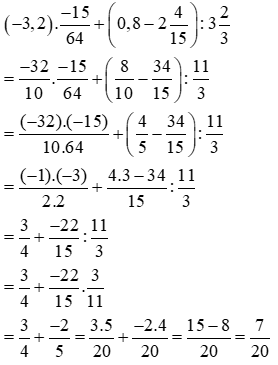Giải Toán 6 trang 46, 47, 48, 49, 50 SGK tập 2: Hỗn số - Số thập phân - Phần trăm
Giải Toán lớp 6 SGK tập 2 trang 46, 47, 48, 49, 50: Hỗn số - Số thập phân - Phần trăm bao gồm đáp án và hướng dẫn giải chi tiết tương ứng với từng bài tập trong sách. Lời giải bài tập Toán 6 này sẽ giúp các em học sinh ôn tập các dạng bài tập có trong sách giáo khoa. Sau đây mời các em cùng tham khảo lời giải chi tiết
Lý thuyết Hỗn số - Số thập phân - Phần trăm Toán lớp 6 tập 2
a. Hỗn số
+ Tổng quát: khi ta viết gọn tổng của một số nguyên dương và phân số dương bằng cách bỏ dấu cộng xen giữa chúng thì được gọi là một hỗn số.
+ Số đối của hỗn số này cũng được gọi là một hỗn số.
Như vậy, một hỗn số gồm hai phần: phần nguyên và phần phân số.
Lưu ý. Muốn đổi một phân số dương có tử lớn hơn mẫu thành một hỗn số ta chia tử cho mẫu. Thương tìm được chính là phần nguyên, phần phân số có tử là số dư còn mẫu là mẫu số của phân số đã cho.
b. Phân số thập phân. Số thập phân.
+ Phân số thập phân là phân số có mẫu là một lũy thừa của 10.
+ Các phân số thập phân có thể viết dưới dạng số thập phân.
+ Số thập phân gồm hai phần:
- Phần số nguyên viết bên trái dấu phẩy;
- Phần thập phân viết bên phải dấu phẩy.
Số chữ số thập phân bằng đúng số chữ số 0 ở mẫu của phân số thập phân.
c. Phần trăm
Phân số có mẫu là 100 được viết dưới dạng phần trăm, tức là dạng gồm tử số của phân số đã cho kèm theo kí hiệu %.
Giải bài 94 trang 46 SGK Toán lớp 6 tập 2
Viết các phân số sau dưới dạng hỗn số:
Hướng dẫn:
Để chuyển một phân số (có tử số lớn hơn mẫu số) sang hỗn số, ta làm như sau:
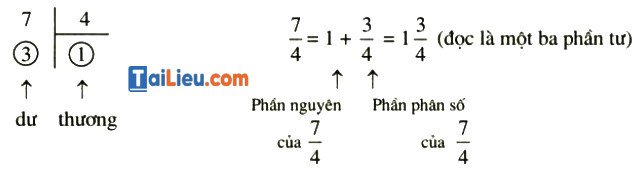
Lời giải:
Giải bài 95 trang 46 Toán lớp 6 tập 2 SGK
Viết các hỗn số sau dưới dạng phân số:
Hướng dẫn:
Để chuyển một hỗn số thành phân số, ta làm như sau:
Lời giải:
Giải bài 96 trang 46 Toán lớp 6 SGK tập 2
So sánh các phân số:
Hướng dẫn:
Viết các phân số dưới dạng hỗn số, nếu các hỗn số có phần nguyên giống nhau thì ta so sánh phần phân số.
Lời giải:
Có
Vì
Giải bài 97 trang 46 SGK tập 2 Toán lớp 6
Đổi ra mét (viết kết quả dưới dạng phân số thập phân rồi dưới dạng số thập phân).
3dm, 85cm, 52mm.
Hướng dẫn:
1dm =
Lời giải:
3dm =
Giải bài 98 trang 46 SGK Toán 6 tập 2
Dùng phần trăm với kí hiệu % để viết các số phần trăm trong các câu sau đây :
Để đạt tiêu chuẩn công nhận phổ cập giáo dục THCS, xã Bình Minh đã đề ra chỉ tiêu phấn đấu:
- Huy động số trẻ 6 tuổi đi học lớp 1 đạt chín mươi mốt phần trăm. Có ít nhất tám mươi hai phần trăm số trẻ ở độ tuổi 11 - 14 tốt nghiệp Tiểu học;
- Huy động chín mươi sáu phần trăm học sinh tốt nghiệp Tiểu học hàng năm vào lớp 6 THCS phổ thông và THCS bổ túc;
- Bảo đảm tỉ lệ học sinh tốt nghiệp THCS hàng năm từ chín mươi tư phần trăm trở lên.
Hướng dẫn:
Phân số có mẫu là 100 được viết dưới dạng phần trăm, tức là dạng gồm tử số của phân số đã cho kèm theo kí hiệu %.
Lời giải:
- Huy động số trẻ 6 tuổi đi học lớp 1 đạt 91%. Có ít nhất 82% số trẻ ở độ tuổi 11 - 14 tốt nghiệp Tiểu học;
- Huy động 96% học sinh tốt nghiệp Tiểu học hàng năm vào lớp 6 THCS phổ thông và THCS bổ túc;
- Bảo đảm tỉ lệ học sinh tốt nghiệp THCS hàng năm từ 94% trở lên.
Giải bài 99 trang 47 Toán 6 tập 2 SGK
Khi cộng hai hỗn số
a) Bạn Cường đã tiến hành cộng hai hỗn số như thế nào?
b) Có cách nào tính nhanh hơn không?
Hướng dẫn:
Muốn cộng hai hỗn số có hai cách như sau:
Cách 1: cộng hai phần nguyên với nhau, 2 phần phân số với nhau. Kết quả tìm được chính là ghép phần nguyên và phần phân số vừa thu được.
Cách 2: ta có thể đưa về dạng phân số rồi cộng các phân số với nhau.
Lời giải:
a) Bạn Cường đã tiến hành cộng hai hỗn số bằng cách đổi các hỗn số về dạng phân số và thực hiện phép cộng phân số.
b) Cách nhanh hơn: cộng hai phần nguyên với nhau, 2 phần phân số với nhau. Kết quả tìm được chính là ghép phần nguyên và phần phân số vừa thu được.
Giải bài 100 trang 47 SGK Toán lớp 6 tập 2
Tính giá trị của các biểu thức:
Hướng dẫn:
Để cộng (trừ) hai hỗn số có hai cách như sau:
Cách 1: cộng (trừ) hai phần nguyên với nhau, 2 phần phân số với nhau. Kết quả tìm được chính là ghép phần nguyên và phần phân số vừa thu được.
Cách 2: ta có thể đưa về dạng phân số rồi cộng (trừ) các phân số với nhau.
Lời giải:
Giải bài 101 trang 47 Toán 6 SGK tập 2
Thực hiện phép nhân hoặc chia hai hỗn số bằng cách viết hỗn số dưới dạng phân số:
| a) | b) |
Hướng dẫn:
Đổi các hỗn số về dạng phân số và thực hiện phép nhân và chia phân số.
Lời giải:
Giải bài 102 trang 47 SGK tập 2 Toán 6
Bạn Hoàng làm phép nhân
Có cách nào tính nhanh hơn không? Nếu có, hãy giải thích cách làm đó.
Hướng dẫn:
Muốn nhân hỗn số với một số nguyên ta có thể nhân phần nguyên với số nguyên, phần phân số với số nguyên rồi cộng các kết quả với nhau
Lời giải:
Giải bài 103 trang 47 SGK Toán lớp 6 tập 2
a) Khi chia một số cho 0,5 ta chỉ việc nhân số đó với 2.
Ví dụ: 37 : 0,5 = 37.2 = 74
102 : 0,5 = 102.2 = 204
Hãy giải thích tại sao lại làm như vậy?
b) Hãy tìm hiểu các làm tương tự khi chia một số cho 0,25; cho 0,125.
Cho các ví dụ minh họa.
Hướng dẫn:
Chuyển các số thập phân về dạng phân số.
Khi thực hiện phép chia phân số, ta nhân với nghịch đảo của phân số đó.
Lời giải:
a) Vì
b) Vì
Ví dụ: 15 : 0,25 = 15.4 = 60
Vì
ví dụ: 25 : 0,125 = 25.8 = 200
Giải bài 104 trang 47 Toán 6 tập 2 SGK
Viết các phân số sau dưới dạng số thập phân và dùng kí hiệu %:
Hướng dẫn:
Phân số có mẫu là 100 được viết dưới dạng phần trăm, tức là dạng gồm tử số của phân số đã cho kèm theo kí hiệu %.
Lời giải:
Giải bài 105 trang 47 Toán 6 SGK tập 2
Viết các phần trăm sau dưới dạng số thập phân:
7%; 45%; 216%
Hướng dẫn:
Phân số có mẫu là 100 được viết dưới dạng phần trăm, tức là dạng gồm tử số của phân số đã cho kèm theo kí hiệu %.
Lời giải:
Giải bài 106 trang 48 SGK Toán 6 tập 2
Hoàn thành các phép tính sau:
Hướng dẫn:
Thực hiện phép cộng và trừ phân số để hoàn thành phép tính.
Lời giải:
Giải bài 107 trang 48 SGK Toán lớp 6 tập 2
Tính:
| a) | b) |
| c) | d) |
Hướng dẫn:
Thực hiện các phép tính cộng, trừ phân số bằng cách quy đồng mẫu số.
Lời giải:
Giải bài 108 trang 48 Toán lớp 6 SGK tập 2
Hoàn thành các phép tính sau:
a) Tính tổng:
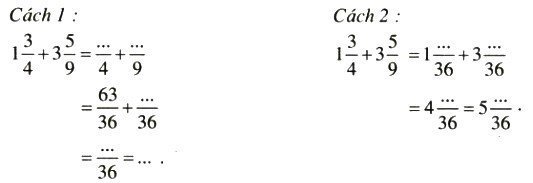
b) Tính hiệu:
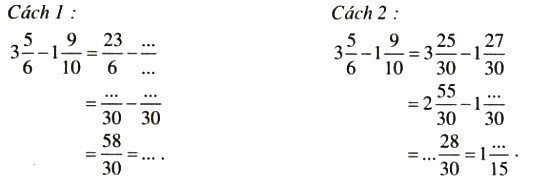
Hướng dẫn:
Để cộng (trừ) hai hỗn số có hai cách như sau:
Cách 1: cộng (trừ) hai phần nguyên với nhau, 2 phần phân số với nhau. Kết quả tìm được chính là ghép phần nguyên và phần phân số vừa thu được.
Cách 2: ta có thể đưa về dạng phân số rồi cộng (trừ) các phân số với nhau.
Lời giải:
a)
Cách 1:
Cách 2:
b)
Cách 1:
Cách 2:
Giải bài 109 trang 49 SGK Toán 6 tập 2
Tính bằng hai cách:
| a) | b) | c) |
Hướng dẫn:
Để cộng (trừ) hai hỗn số có hai cách như sau:
Cách 1: cộng (trừ) hai phần nguyên với nhau, 2 phần phân số với nhau. Kết quả tìm được chính là ghép phần nguyên và phần phân số vừa thu được.
Cách 2: ta có thể đưa về dạng phân số rồi cộng (trừ) các phân số với nhau.
Lời giải:
a)
Cách 1:
Cách 2:
b)
Cách 1:
Cách 2:
c)
Cách 1:
Cách 2:
Giải bài 110 trang 49 SGK Toán lớp 6 tập 2
Áp dụng tính chất các phép tính và quy tắc dấu ngoặc để tính giá trị các biểu thức sau:
Lời giải:
Giải bài 111 trang 49 SGK Toán 6 tập 2
Tìm số nghịch đảo của các số sau:
Lời giải:
Hướng dẫn giải:
+ Số a được gọi là số nghịch đảo của b nếu a.b = 1.
+ Số nghịch đảo của 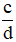
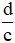
Giải bài 112 trang 49 Toán lớp 6 tập 2 SGK
Hãy kiểm tra các phép cộng sau đây rồi sử dụng kết quả của các phép cộng này để điền số thích hợp vào ô trống mà không cần tính toán:
Hướng dẫn giải:
+ Tính chất giao hoán của phép cộng phân số:
+ Tính chất kết hợp của phép cộng phân số:
+ Kết hợp cả tính chất giao hoán và tính chất kết hợp:
Lời giải:
- Các phép cộng đều cho kết quả đúng.
- Ta có:
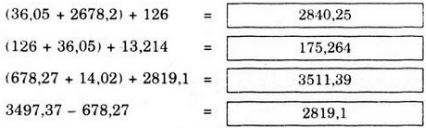
(36,05 + 2678,2) + 126
= 36,05 + (2678,2 + 126) (Tính chất kết hợp)
= 36,05 + 2804,2 (theo a)
= 2840,25 (theo c)
(126 + 36,05) + 13,214
= 126 + (36,05 + 13,214) (tính chất kết hợp)
= 126 + 49,264 (theo b)
= 175,264 (theo d)
(678,27 + 14,02) + 2819,1
= (678,27 + 2819,1) + 14,02 (Tính chất giao hoán và kết hợp)
= 3497,37 + 14,02 (theo e)
= 3511,39 (theo g)
3497,37 – 678,27 = 2819,1 (suy từ e)
Vì vậy ta có thể điền số thích hợp và ô trống mà không cần tính toán:
Giải bài 113 trang 50 Toán 6 SGK tập 2
Hãy kiểm tra các phép nhân sau đây rồi sử dụng kết quả của các phép tính này để điền số thích hợp vào ô trống mà không cần tính toán:
Hướng dẫn giải:
+ Tính chất giao hoán của phép nhân phân số:
+ Tính chất kết hợp của phép nhân phân số:
+ Kết hợp cả tính chất giao hoán và tính chất kết hợp:
+ Nếu có b, c là các số khác 0. Khi đó : a : (b . c) = a : b : c.
Lời giải:
- Các phép nhân đều cho kết quả đúng.
- Ta có:
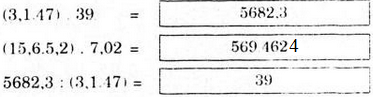
(3,1 . 47) . 39 = 3,1 .(47 . 39) (tính chất kết hợp)
= 3,1 .1833 (theo a)
= 5682,3 (theo c)
(15,6 . 5,2) . 7,02 = (15,6 . 7,02) . 5,2 (Tính chất giao hoán và kết hợp)
= 109,512 . 5,2 (theo b)
= 569,4624 (theo d)
5682,3 : (3,1 . 47) = (5682,3 : 3,1) : 47
= 1833 : 47 (suy từ c) = 39 (suy từ a)
Vì vậy ta có thể điền các số thích hợp vào ô trống mà không cần tính toán.
Giải bài 114 trang 50 SGK Toán 6 tập 2
Tính:
Lời giải:
►► CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải bài tập toán lớp 6 trang 46, 47, 48, 49, 50 tập 2 file word, pdf hoàn toàn miễn phí
- Giải Toán lớp 6 Bài 2: Phân số bằng nhau (Tập 2) | Hay nhất
- Giải Bài 3: Tính chất cơ bản của phân số lớp 6 (Tập 2)
- Giải bài tập Toán lớp 6 trang 75 Bài 2: Góc (Tập 2) chi tiết
- Giải bài tập Toán hình lớp 6 Bài 1 2 3 4 5 - Nửa mặt phẳng (Tập 2)
- Giải Toán lớp 6 trang 33, 34, 35 SGK tập 2: Phép trừ phân số
- Giải Toán lớp 6 trang 36, 37 SGK tập 2: Phép nhân phân số
- Giải Toán lớp 6 trang 64, 65 SGK tập 2: Ôn tập chương 3
- Giải Toán 6 trang 38, 39, 40, 41 SGK tập 2: Tính chất cơ bản của phép nhân phân số