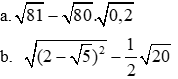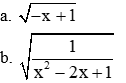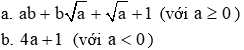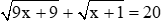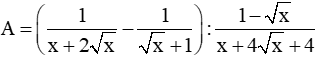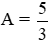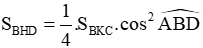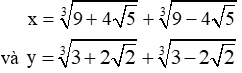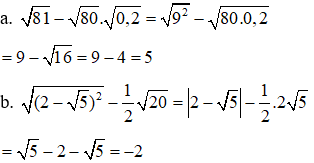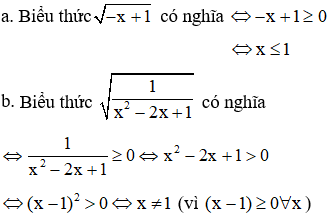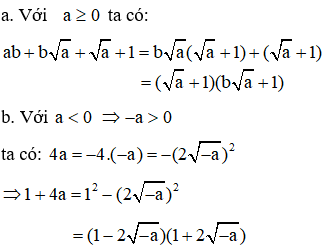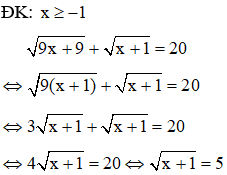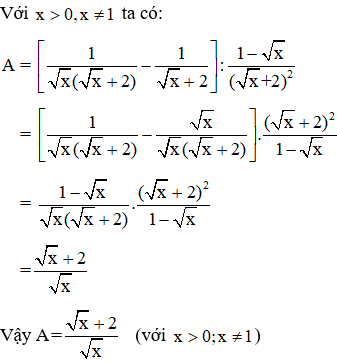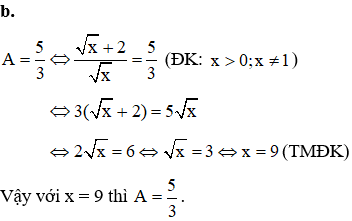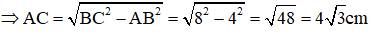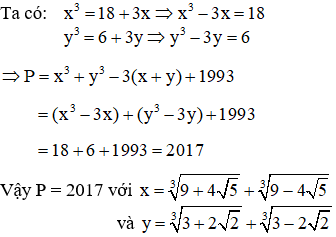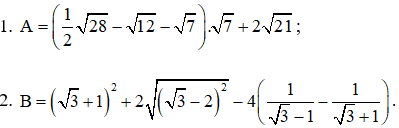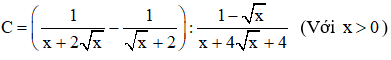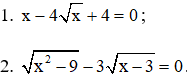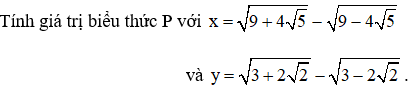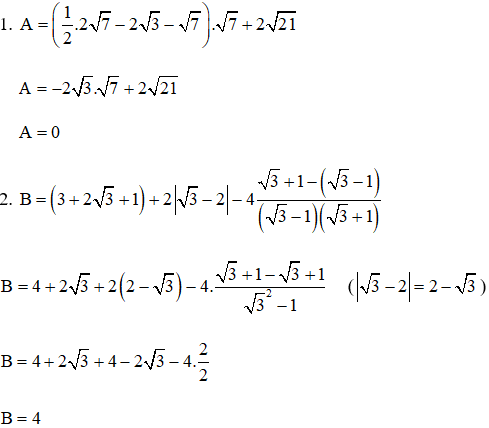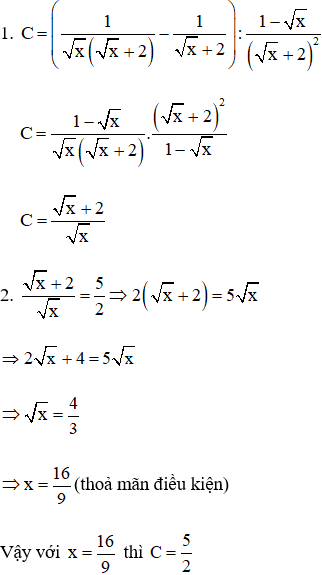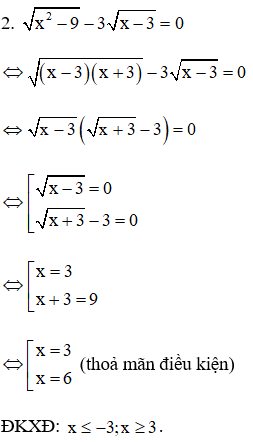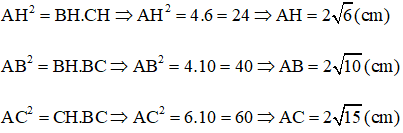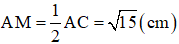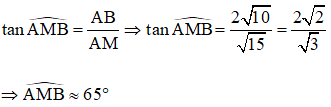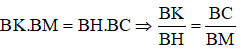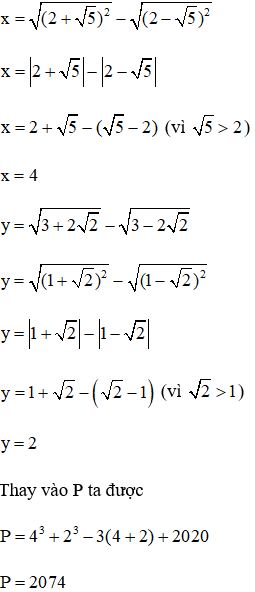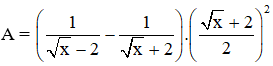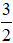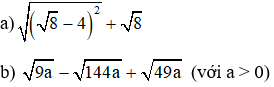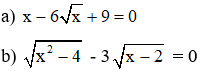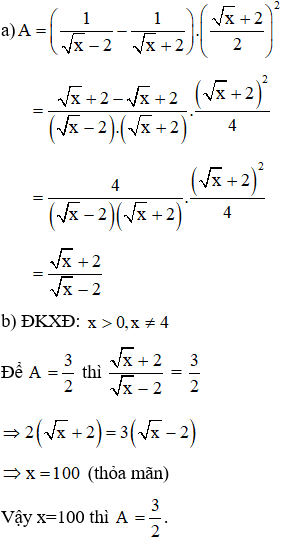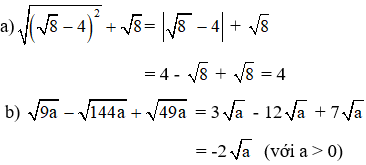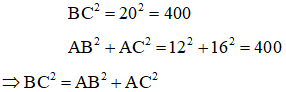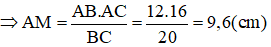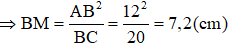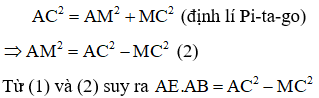Bộ đề kiểm tra giữa kì 1 Toán 9 năm 2021 - 2022 (có đáp án) Phần 1

Giới thiệu đến các em học sinh và quý thầy cô giáo bộ tài liệu ôn thi giữa học kì 1 môn Toán lớp 9 có đáp án và hướng dẫn giải chi tiết. Các bạn có thể tải về bản PDF hoặc Word miễn phí tại đường link cuối bài.

Đề thi Toán giữa kì 1 lớp 9 năm 2021 - 2022 (Đề số 1)

Bài 1 (2,0 điểm).

1. Thực hiện phép tính.

2. Tìm điều kiện của x để các biểu thức sau có nghĩa:

Bài 2 (2,0 điểm).

1. Phân tích đa thức thành nhân tử.

2. Giải phương trình: 

Bài 3 (2,0 điểm. Cho biểu thức:  

(với x > 0; x ≠ 1)

a. Rút gọn biểu thức A.

b. Tìm x để  

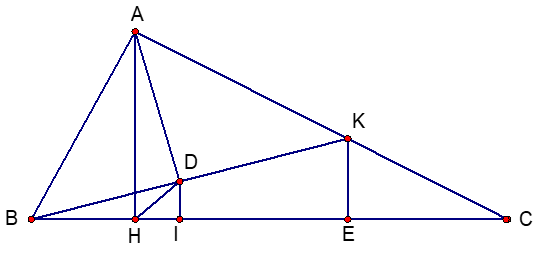
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.

a. Tính độ dài các đoạn thẳng AB, AC, AH.

b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.

c. Chứng minh rằng: 

Bài 5 (0,5 điểm).

Cho biểu thức P = x³ + y³ - 3(x + y) + 1993. Tính giá trị biểu thức P với:

Hướng dẫn giải chi tiết

Bài 1.

1. Thực hiện phép tính

2. Tìm điều kiện của x để biểu thức có nghĩa

Bài 2.

1. Phân tích đa thức thành nhân tử:

2. Giải phương trình

⇔ x + 1 = 25 ⇔ x = 24 (thỏa mãn điều kiện xác định)

Vậy phương trình có nghiệm duy nhất x = 24

Bài 3.

a. Rút gọn biểu thức

Bài 4.

a.

Ta có ΔABC vuông tại A, đường cao AH

⇒ AB² = BH.BC = 2.8 = 16 (hệ thức lượng trong tam giác vuông)

⇒  AB = 4cm (Vì AB > 0)

Mà BC² = AB² + AC² (Định lý Pitago trong tam giác vuông ABC)

Có HB + HC = BC ⇒ HC = BC – HB = 8 – 2 = 6 cm

Mà AH² = BH.CH = 2.6 = 12 (hệ thức lượng trong tam giác vuông)

⇒   (Vì AH > 0)

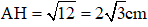
b.

Ta có ΔABK vuông tại A có đường cao AD

⇒ AB² = BD.BK (1)

Mà AB² = BH.BC (chứng minh câu a)  (2)

Từ (1) và (2) suy ra BD.BK = BH.BC

c.

Bài 5.

Đề thi giữa học kì 1 Toán 9 năm 2021 - 2022 (Đề số 2)

Bài 1. (2 điểm) Tính giá trị của biểu thức:

Bài 2.(2 điểm) Cho biểu thức:

1. Rút gọn C;

2. Tìm x để .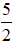

Bài 3.(2 điểm) Giải phương trình

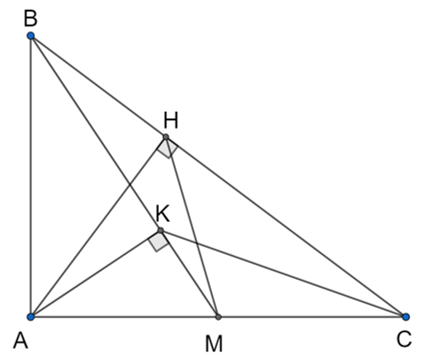
Bài 4.(3,5 điểm) Cho tam giác ABC vuông tại A có đường cao AH. Độ dài BH = 4cm và HC = 6cm.

1. Tính độ dài các đoạn AH, AB, AC.

2. Gọi M là trung điểm của AC. Tính số do góc AMB (làm tròn đến độ).

3. Kẻ AK vuông góc với BM (K ∈ BM). Chứng minh: ΔBKC đồng dạng với ΔBHM.

Bài 5.(0,5 điểm) Cho biểu thức: P = x³ + y³ - 3(x + y) + 2020

Hướng dẫn giải chi tiết

Bài 1.

Bài 2.

Bài 3.

ĐKXĐ: x ≤ -3; x ≥ 3. Vậy nghiệm của phương trình là x = 3 và x = 6.

Bài 4.

1. ΔABC vuông tại A, có đường cao AH.

Áp dụng hệ thức lượng trong tam giác vuông:

2. Do M là trung điểm của AC nên 

Xét ABM vuông tại A:

3. Xét ΔABM vuông tại A, có AK là đường cao

Áp dụng hệ thức lượng trong tam giác vuông

  AB² = BK.BM (1)

ΔABC vuông tại A, có đường cao AH.

Áp dụng hệ thức lượng trong tam giác vuông

  AB² = BH.BC (2)

Từ (1) và (2) ta có:

  

Xét ΔBKC và ΔBHM có:

  

⇒ ΔBKC đồng dạng với ΔBHM (c.g.c) (đpcm)

Bài 5.

Đề thi Toán 9 giữa học kì 1 năm 2021 - 2022 (Đề số 3)

Bài 1 (2,5 điểm). Cho biểu thức:

a) Rút gọn biểu thức

b) Tìm giá trị của x để A = 

Bài 2 (2 điểm). Thực hiện phép tính:

Bài 3 (2 điểm). Giải phương trình:

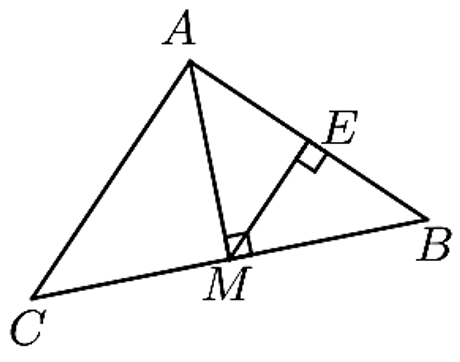
Bài 4 (3,5 điểm). Cho tam giác ABC có cạnh AB = 12cm, AC = 16cm, BC = 20cm. Kẻ đường cao AM. Kẻ ME vuông góc với AB.

a) Chứng minh tam giác ABC là tam giác vuông.

b) Tính độ dài AM, BM.

c) Chứng minh AE.AB = AC² - MC²

d) Chứng minh AE.AB = MB.MC = EM.AC

Hướng dẫn giải chi tiết:

Bài 1.

Bài 2.

Bài 3.

Vậy tập nghiệm của phương trình là S = {2;7}

Bài 4.

a)

Xét tam giác ABC có:

Nên tam giác ABC vuông tại A (theo định lí Pi-ta-go đảo)

b)

+ Xét tam giác ABC vuông tại A (cmt) có AM là đường cao nên:

AM. BC = AB. AC (hệ thức lượng trong tam giác vuông)

+ Lại có: AB² = BM. BC (hệ thức lượng trong tam giác vuông)

c) Xét tam giác AMB vuông tại M có ME là đường cao nên:

AE. AB = AM² (hệ thức lượng trong tam giác vuông) (1)

Xét tam giác AMC vuông tại M có:

d)

+ Xét tam giác ABC vuông tại A có AM là đường cao nên

MB.MC = MA² (hệ thức lượng trong tam giác vuông)

Lại có AE.AB = AM² (cmt)

Do đó AE.AB = AC.EM = MB.MC = AM²

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Bộ đề thi giữa kì 1 Toán 9 năm 2021 - 2022 (có đáp án) Phần 1 file PDF hoàn toàn miễn phí.