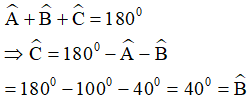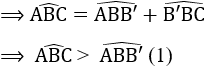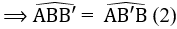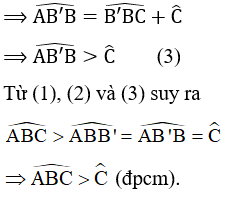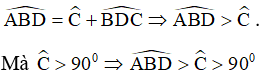Giải toán lớp 7 trang 53 - 56 SGK tập 2 đầy đủ nhất

Hướng dẫn giải Toán lớp 7: Quan hệ giữa góc và cạnh đối diện trong một tam giác trang 53 - 56 sách giáo khoa được trình bày chi tiết, dễ hiểu dưới đây sẽ giúp các em tham khảo và vận dụng giải các bài tập cùng dạng toán hiệu quả nhất.

Trả lời câu hỏi Toán 7 Tập 2 Bài 1 trang 53 SGK

Vẽ tam giác ABC với AC > AB. Quan sát hình và dự đoán xem ta có trường hợp nào trong các trường hợp sau:

1) ∠B = ∠C

2) ∠B > ∠C

3) ∠B < ∠C .

Lời giải

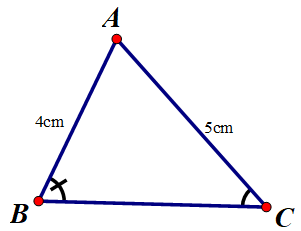
Ta vẽ ΔABC có AB = 4 cm; AC = 5 cm

Quan sát hình, ta dự đoán xảy ra trường hợp 2) ∠B > ∠C

Trả lời câu hỏi Toán lớp 7 Tập 2 Bài 1 trang 53

Gấp hình và quan sát:

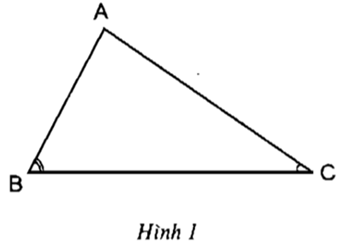
• Cắt một tam giác ABC bằng giấy với AC > AB (h.1)

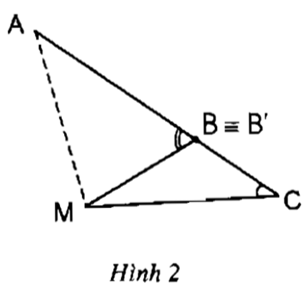
• Gấp tam giác ABC từ đỉnh A sao cho cạnh AB chồng lên cạnh AC để xác định tia phân giác AM của góc BAC, khi đó điểm B trùng với một điểm B’ trên cạnh AC (h.2).

Hãy so sánh góc AB’M và góc C.

Lời giải

Ta có: góc AB’M là góc ngoài của tam giác MB’C

Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C

Trả lời câu hỏi Toán 7 Tập 2 SGK Bài 1 SGK trang 55

Vẽ tam giác ABC với B^ > C^. Quan sát hình và dự đoán xem ta có trường hợp nào trong các trường hợp sau:

1) AB = AC

2) AB > AC

3) AC > AB.

Lời giải

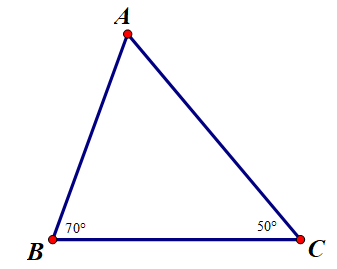
Ta vẽ tam giác ABC có ∠B = 70o; ∠C = 50o

Quan sát hình, ta dự đoán xảy ra trường hợp 3) AC > AB

Giải Bài 1 trang 55 SGK Toán 7 tập 2

So sánh các góc của tam giác ABC, biết rằng:

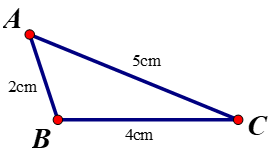
AB = 2cm,     BC = 4cm,     AC = 5cm

Lời giải:

Dựa vào hình vẽ, ta có:

Góc đối diện cạnh BC là Â

Góc đối diện cạnh AC là B̂

Góc đối diện cạnh AB là Ĉ

Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn

Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.

Giải Bài 2 trang 55 SGK Toán lớp 7 tập 2

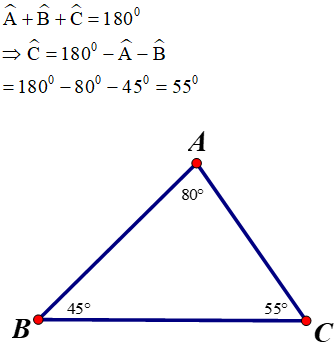
So sánh các cạnh của tam giác ABC, biết rằng: Â = 80º, B̂ = 45º

Lời giải:

Theo định lý tổng ba góc trong tam giác ABC, ta có:

Cạnh đối diện góc B là AC

Cạnh đối diện góc C là AB

Cạnh đối diện góc A là BC

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.

Giải Bài 3 Toán 7 tập 2 trang 56 SGK 

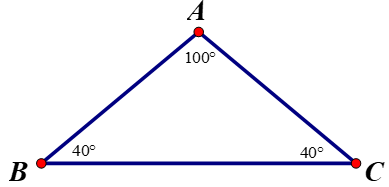
Cho tam giác ABC với góc A = 100o, góc B = 40o.

a) Tìm cạnh lớn nhất của tam giác ABC.

b) Tam giác ABC là tam giác gì?

Lời giải:

a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.

Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.

b) Tam giác ABC là tam giác tù vì có 1 góc A tù.

Áp dụng định lý tổng ba góc trong tam giác ABC ta có:

Suy ra ∆ABC cân tại A.

Giải Bài 4 SGK Toán 7 tập 2 trang 56 

Trong một tam giác, đối diện với cạnh nhỏ nhất là góc gì (nhọn, vuông, tù)? Tại sao?

Lời giải:

Trong một tam giác ta luôn có:

+ Góc đối diện với cạnh lớn hơn là góc lớn hơn

⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.

+ Góc nhỏ nhất luôn là góc nhọn.

(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn

⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.

Điều này vô lý vì tổng ba góc trong tam giác = 180º).

Do đó góc đối diện với cạnh nhỏ nhất là góc nhọn.

Giải Toán 7 tập 2 Bài 5 trang 56 SGK

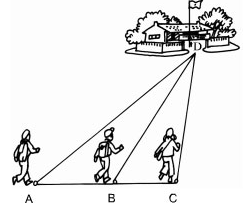
Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường AD, BD, và CD (h.5). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng và góc ACD là góc tù.

Hỏi ai đi xa nhất, ai đi gần nhất? Hãy giải thích.

Hình 5

Lời giải:

+ Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).

+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :

Giải Bài 6 tập 2 trang 56 SGK Toán 7

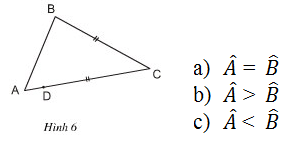
Xem hình 6, có hai đoạn bằng nhau BC và DC. Hỏi rằng kết luận nào trong các kết luận sau là đúng? Tại sao?

Lời giải:

Vì D nằm giữa A và C (giả thiết)

⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)

⇒ AC > BC

Mà trong tam giác ABC :

Góc đối diện cạnh AC là góc B

Góc đối diện cạnh BC là góc A

Giải Bài 7 SGK Toán 7 trang 56 tập 2

Một cách chứng minh khác của định lí 1:

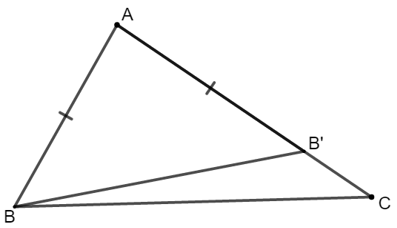
Cho tam giác ABC với AC > AB. Trên tia AC, lấy điểm B' sao cho AB' = AB.

a) Hãy so sánh góc ABC với góc ABB'.

b) Hãy so sánh góc ABB' với góc AB'B.

c) Hãy so sánh góc AB'B với góc ACB.

Lời giải:

a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.

⇒ tia B’B nằm giữa hai tia BA và BC.

b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.

c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C

Ta lại có: AC > BC (cmt)

⇒ B̂ > Â (theo định lí 1)

Hay  < B̂.

Vậy kết luận c) là đúng.

nên góc ABD cũng là góc tù.

Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD

(2).

Từ (1) và (2) suy ra AD > BD > CD.

Vậy Hạnh đi xa nhất, Trang đi gần nhất.

CLICK NGAY vào nút TẢI VỀ dưới đây để tải giải toán lớp 7 trang 53 - 56 file word, pdf hoàn taofn miễn phí