Giải toán lớp 7 trang 86, 87 SGK tập 2: Ôn tập chương III

Hướng dẫn giải bài tập từ trang 86, 87 sách giáo khoa Toán lớp 7 tập 2 bài Ôn tập chương III - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác được trình bày chi tiết, chính xác và dễ hiểu dưới đây bao gồm nội dung trả lời các câu hỏi và giải bài tập giúp các em học sinh củng cố kiến thức, vận dụng giải các dạng toán tương tự hiệu quả nhất.

Giải bài 1 trang 86 SGK Toán lớp 7 tập 2 

Đề bài

Cho tam giác ABC. Hãy viết kết luận của hai bài toán sau về quan hệ giữa góc và cạnh đối diện trong một tam giác.

Lời giải chi tiết

Giải bài 2 SGK trang 86 Toán 7 tập 2

Đề bài

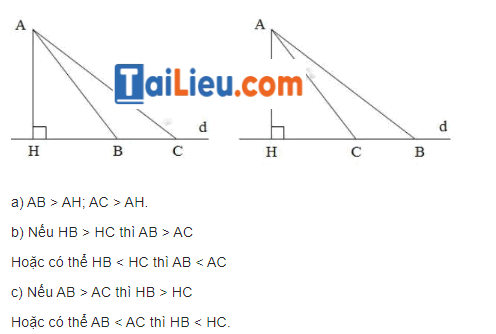
Từ điểm A không thuộc đường thẳng d, kẻ đường vuông góc AH, các đường xiên AB, AC đến đường thẳng d. Hãy điền dấu (<, >) vào các chỗ trống (…) dưới đây cho đúng:

a) AB … AH ; AC … AH.

b) Nếu HB … HC thì AB … AC.

c) Nếu AB … AC thì HB … HC.

Lời giải chi tiết

Giải bài 3 trang 86 tập 2 SGK Toán 7

Đề bài

Cho tam giác DEF. Hãy viết các bất đẳng thức về quan hệ giữa các cạnh của tam giác này.

Lời giải chi tiết

Với ∆DEF, giả sử DE < EF < DF, ta có các bất đẳng thức về quan hệ giữa các cạnh là:

+) DF – EF < DE < EF + DF

+) EF - DE < DF < EF + DE

+) DF - DE < EF < DE + DF

Giải bài 4 tập 2 trang 86 SGK Toán 7 

Đề bài

Hãy ghét đôi hai ý ở hai cột để được khẳng định đúng

Lời giải chi tiết

Ghép a – d’ ; b – a’ ; c – b’ ; d – c’.

Giải bài 5 Toán 7 tập 2 trang 86 SGK 

Đề bài

Hãy ghét đôi hai ý ở hai cột để được khẳng định đúng

Lời giải chi tiết

Ghép a – b’, b – a’, c – d’, d – c’.

Giải bài 6 trang 87 SGK Toán 7 tập 2

Đề bài

a) Hãy nêu tính chất của trọng tâm của một tam giác; các cách xác định trọng tâm.

b) Bạn Nam nói: Có thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác. Bạn Nam nói đúng hay sai?Tại sao?

Lời giải chi tiết

a) - Trọng tâm của một tam giác có tính chất như sau:

Trọng tâm cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.

- Các cách xác định trọng tâm

+ Cách 1: Vẽ hai đường trung tuyến ứng với hai cạnh tùy ý, rồi xác định giao điểm của hai đường trung tuyến đó.

+ Cách 2: Vẽ một đường trung tuyến của tam giác. Chia độ dài đường trung tuyến đó thành ba phần bằng nhau rồi xác định một điểm cách đỉnh hai phần bằng nhau.

b) Không thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác vì đường trung tuyến đi qua một đỉnh của tam giác và trung điểm một cạnh trong tam giác nên đường trung tuyến phải nằm giữa hai cạnh của tam giác tức nằm ở miền trong của tam giác nên ba đường trung tuyến cắt nhau chỉ có thể nằm ở bên trong của tam giác.

Giải bài 7 trang 87 SGK Toán 7 

Đề bài

Những tam giác nào có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao?

Lời giải chi tiết

Tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân.

Giải bài 8 Toán lớp 7 trang 87 SGK tập 2

Đề bài

Những tam giác nào có trọng tâm đồng thời là trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh?

Lời giải chi tiết

Tam giác có trọng tâm đồng thời là trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh là tam giác đều.

Giải Toán lớp 7 bài 63 trang 87 SGK  tập 2

Đề bài

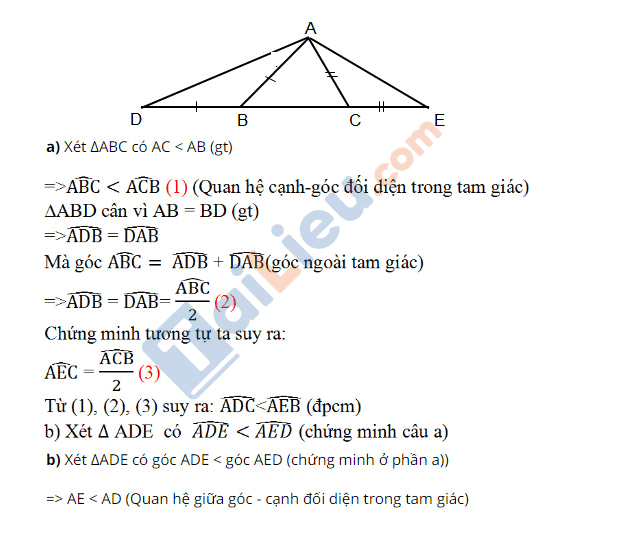
Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.

a) Hãy so sánh góc ADC và góc AEB.

b) Hãy so sánh các đoạn thẳng AD và AE

Lời giải chi tiết

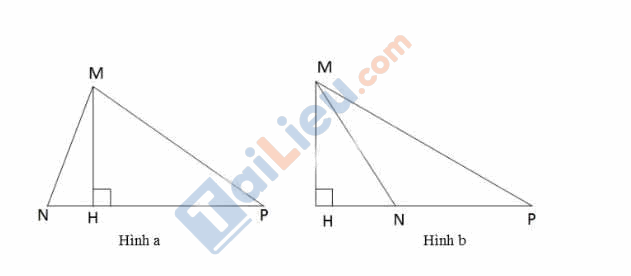
Giải bài 64 trang 87 Toán 7 SGK tập 2

 

Giải bài 65 trang 87 Toán 7 tập 2

Đề bài

Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài như sau: 1cm, 2cm, 3cm, 4cm và 5cm?

Lời giải chi tiết

Để tạo được một tam giác thì độ dài ba cạnh phải thoả mãn bất đẳng thức tam giác đó là tổng độ dài hai cạnh bất kỳ phải lớn hơn cạnh còn lại.

Vì vậy chỉ có bộ ba độ dài sau thoả mãn (2cm; 3cm; 4cm); (2cm; 4cm; 5cm); (3cm; 4cm; 5cm).

(Lưu ý: để xét cho nhanh, các bạn áp dụng phần Lưu ý (trang 63 sgk Toán 7 Tập 2)), tức là ta so sánh độ dài lớn nhất với tổng hai cạnh hoặc so sánh độ dài nhỏ nhất với hiệu hai cạnh.

Ví dụ với cặp 3 độ dài (1cm; 2cm; 3cm) không là ba cạnh của tam giác vì:

- bất đẳng thức 3 > 2 + 1 sai

- hoặc bất đẳng thức 3 - 2 < 1 sai)

Giải bài 66 trang 87 SGK Toán 7 tập 2

Đề bài

Đố: Bốn điểm dân cư được xây dựng như hình 58. Hãy tìm vị trí đặt một nhà máy sao cho tổng các khoảng cách từ nhà máy đến bốn điểm dân cư này là nhỏ nhất.

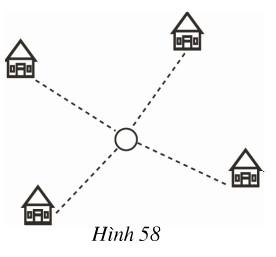
Lời giải chi tiết

Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.

Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: OA + OB + OC + OD.

CLICK NGAY vào nút TẢI VỀ dưới đây để tải Giải toán lớp 7 trang 86, 87 file word, pdf hoàn toàn miễn phí