Giải toán lớp 7 trang 78, 79, 80 SGK tập 2 đầy đủ nhất

Hướng dẫn giải Toán 7 bài 8: Tính chất ba đường trung trực của tam giác trang 78, 79, 80 sách giáo khoa được trình bày chi tiết, dễ hiểu dưới đây sẽ giúp các em tham khảo và vận dụng giải các bài tập cùng dạng toán hiệu quả nhất.

Trả lời câu hỏi Toán 7 Tập 2 Bài 8 trang 78 SGK

Em hãy vẽ hình, viết giả thiết, kết luận và chứng minh định lý trên.

Lời giải

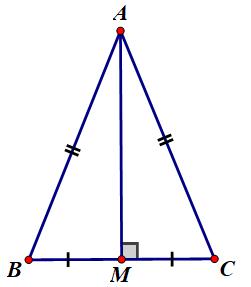
- Giả thiết: ΔABC cân tại A

AM là đường trung trực ứng với cạnh BC

- Kết luận: AM là trung tuyến ứng với cạnh BC

Giải Bài 52 trang 79 SGK Toán 7 tập 2

Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân.

Lời giải:

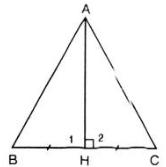
Xét ΔABC với AH là trung tuyến đồng thời là đường trung trực, nên ta có:

AH ⊥ BC và HB = HC

Xét hai tam giác vuông ΔHAB và ΔHAC có:

HB = HC

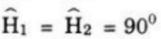
Cạnh AH chung

Vậy ΔHAB = ΔHAC => AB = AC

Hay ΔABC cân tại A (đpcm).

Giải Bài 53 trang 80 SGK Toán lớp 7 tập 2

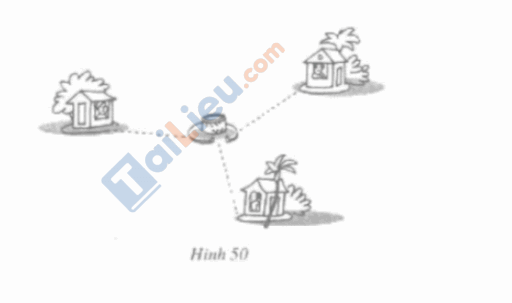
Ba gia đình quyết định đào chung một cái giếng (h.50). Phải chọn vị trí của giếng ở đâu để các khoảng cách từ giếng đến các nhà bằng nhau?

Lời giải:

Giả sử mỗi ngôi nhà là một đỉnh của tam giác ABC chẳng hạn. Để điểm đào giếng cách đều ba ngôi nhà (ba đỉnh của tam giác) thì điểm đó chính là giao điểm ba đường trung trực của tam giác đó (áp dụng định lí giao điểm của ba đường trung trực).

Giải Bài 54 SGK Toán 7 tập 2 trang 80 

Vẽ đường tròn đi qua ba đỉnh của tam giác ABC trong các trường hợp sau:

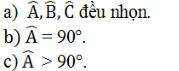
Lời giải:

Tâm đường tròn chính là giao điểm của hai đường trung trực của hai cạnh bất kì trong tam giác ABC.

a) Tam giác có ba góc đều nhọn thì tâm đường tròn nằm trong tam giác.

b) Tam giác vuông thì tâm đường tròn nằm trên cạnh huyền.

c) Tam giác có góc tù thì tâm đường tròn nằm ngoài tam giác.

Giải Toán 7 tập 2 Bài 55 trang 80 SGK

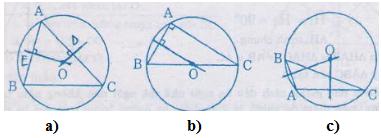
Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.

Hình 51

Lời giải:

Nối BD và CD.

Từ hình vẽ ta có DK là đường trung trực của AC, DI là đường trung trực của AB nên:

BD = AD = CD

Xét ΔADK và ΔCDK có:

AD = CD

DK chung

AK = KC

=> ΔADK = ΔCDK (c.c.c)

Vậy B, D, C thẳng hàng (đpcm).

Giải Bài 56 trang 80 tập 2 SGK Toán 7 

Sử dụng bài 55 để chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.

Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.

Lời giải:

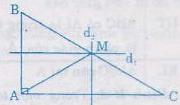
a) Giả sử ΔABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2 của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (Bài tập 55)

Vì M thuộc đường trung trực của AB nên MA = MB. (1)

Vì M thuộc đường trung trực của AC nên MA = MC.

=> MB = MC (2)

Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC

b) Từ (1) và (2) ở câu a) suy ra:

MA = MB = MC = BC/2

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

Giải Bài 57 Toán 7 tập 2 trang 80 SGK

Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy. Làm thế nào để xác định được bán kính của đường viền này?

Lời giải:

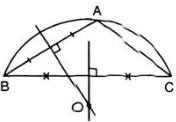
- Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.

- Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC

Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.

CLICK NGAY vào nút TẢI VỀ dưới đây đê tải Giải toán lớp 7 trang 78, 79, 80 file word, pdf hoàn toàn miễn phí