Giải toán lớp 7 trang 61 - 64 SGK tập 2 đầy đủ nhất

Giải Toán lớp 7 SGK tập 2 trang 61 - 64: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác bao gồm đáp án và hướng dẫn giải chi tiết tương ứng với từng bài tập trong sách. Lời giải bài tập Toán 7 này sẽ giúp các em học sinh ôn tập các dạng bài tập có trong sách giáo khoa. Sau đây mời các em cùng tham khảo lời giải chi tiết

Trả lời câu hỏi Toán 7 Tập 2 Bài 3 trang 61 SGK 

Hãy thử vẽ tam giác với các cạnh có độ dài 1cm, 2cm, 4cm. Em có vẽ được không?

Lời giải

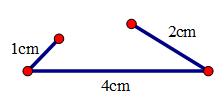
Không vẽ được tam giác thỏa mãn yêu cầu đề bài

Trả lời câu hỏi Toán lớp 7 Tập 2 Bài 3 trang 61

Dựa vào hình 17, hãy viết giả thiết, kết luận của định lý

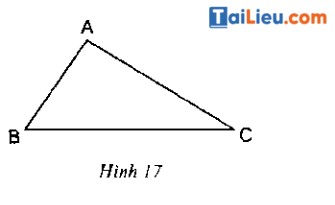
Lời giải

- Giả thiết: ΔABC

- Kết luận:

AB + AC > BC

BC + AC > AB

BC + AB > AC

Trả lời câu hỏi Toán 7 SGK Tập 2 Bài 3 trang 62

Em hãy giải thích vì sao không có tam giác với ba cạnh có độ dài 1cm, 2cm, 4cm (xem câu hỏi 1 trang 61).

Lời giải

Ba cạnh có độ dài 1cm, 2cm, 4cm có: 1cm + 2 cm = 3 cm < 4 cm

Trái với định lí về bất đẳng thức tam giác

⇒ Không có tam giác với ba cạnh có độ dài 1cm, 2cm, 4cm

Giải Bài 15 trang 63 SGK Toán 7 tập 2

Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. Trong những trường hợp còn lại, hãy thử dựng tam giác có độ dài ba cạnh như thế:

a) 2cm, 3cm, 6cm

b) 2cm, 4cm, 6cm

c) 3cm, 4cm, 6cm

Lời giải:

a) Ba độ dài này không phải là ba cạnh của một tam giác vì bất đẳng thức 6 < 3 + 2 sai.

b) Ba độ dài này không phải là ba cạnh của một tam giác vì bất đẳng thức 6 = 2 + 4 sai.

c) Vì ba độ dài thỏa mãn bất đẳng thức 4 – 3 < 6 < 4 + 3 nên chúng là 3 cạnh của một tam giác.

Dựng hình:

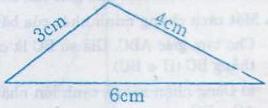
Giả Toán 7 tập 2 Bài 16 trang 63 SGK

Cho tam giác ABC với hai cạnh BC = 1cm, AC = 7cm.

Hãy tìm độ dài cạnh AB, biết rằng độ dài này là một số nguyên (cm). Tam giác ABC là tam giác gì?

Lời giải:

Theo bất đẳng thức tam giác ABC ta có:

AC – BC < AB < AC + BC

Thay BC = 1cm, AC = 7cm, ta được:

7 – 1 < AB < 7 + 1

6 < AB < 8 (1)

Vì độ dài AB là một số nguyên (cm) thỏa mãn (1) nên AB = 7cm

Vì AB = AC = 7cm nên ΔABC cân tại A

Giải Bài 17 Toán 7 tập 2 trang 63 SGK 

Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC.

a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA.

b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB.

c) Chứng minh bất đẳng thức MA + MB < CA + CB.

Lời giải:

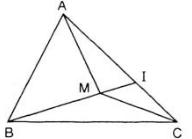
a) Trong ΔAMI ta có: MA < MI + IA

Cộng MB vào hai vế ta được:

MA + MB < MB + MI + IA

Vì MB + MI = IB nên MA + MB < IB + IA (1) (đpcm)

b) Trong ΔBIC ta có: IB < IC + CB

Cộng IA vào hai vế ta được:

IB + IA < IA + IC + CB

Vì IA + IC = CA nên IB + IA < CA + CB (2) (đpcm)

c) Từ (1) và (2) và theo tính chất bắc cầu ta suy ra:

MA + MB < CA + CB (đpcm)

Giải Bài 18 SGK trang 63 Toán 7 tập 2

Cho các bộ ba đoạn thẳng có độ dài như sau:

a) 2cm; 3cm; 4cm

b) 1cm; 2cm; 3,5cm

c) 2,2cm; 2cm; 4,2cm

Hãy vẽ tam giác có độ dài ba cạnh lần lượt là một trong các bộ ba ở trên (nếu vẽ được). Trong trường hợp không vẽ được hãy giải thích.

Lời giải:

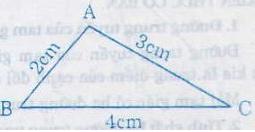
a) Ba độ dài thỏa mãn bất đẳng thức: 3 - 2 < 4 < 2 + 3 nên chúng là ba cạnh của một tam giác.

Vẽ tam giác:

b) Ba độ dài không là ba cạnh của tam giác vì bất đẳng thức 3,5 < 1 + 2 sai.

c) Ba độ dài không là ba cạnh của tam giác vì bất đẳng thức 4,2 = 2,2 + 2 sai.

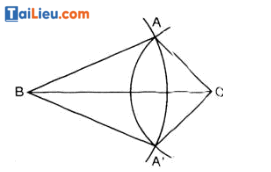
Tham khảo cách vẽ hình câu a)

Vẽ đoạn thẳng BC = 4cm. Lấy B làm tâm vẽ cung tròn có bán kính bằng 3cm và lấy C làm tâm vẽ cung tròn có bán kính bằng 2cm. Hai cung tròn cắt nhau tại hai điểm A và A'. Ta được ΔABC và ΔA'BC là hai tam giác cần vẽ.

Giải Bài 19 Toán 7 tập 2 trang 63 SGK

Tìm chu vi của một tam giác cân biết độ dài hai cạnh của nó là 3,9cm và 7,9cm.

Lời giải:

Cạnh 3,9cm không thể là cạnh bên vì bất đẳng thức 7,9 < 3,9 + 3,9 sai.

Vậy cạnh bên là 7,9cm nên chu vi tam giác là:

3,9 + 7,9 + 7,9 = 19,7cm

Giải Bài 20 Toán 7 trang 64 SGK tập 2

Một cách chứng minh khác của bất đẳng thức tam giác:

Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).

a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.

b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.

Lời giải:

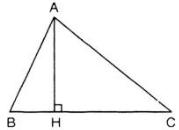
a) Ta biết rằng trong tam giác vuông thì cạnh huyền là cạnh lớn nhất, do đó:

Trong ΔAHC vuông tại H ta có: HC < AC

Trong ΔAHB vuông tại H ta có: HB < AB

Cộng vế theo vế hai bất đẳng thức ta có:

HB + HC < AC + AB

Vì HB + HC = BC nên BC < AC + AB ()

b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC

Vì AB, AC > 0 nên AB < BC + AC; AC < BC + AB (đpcm)

(Cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

Giải Toán 7 tập 2 Bài 21 trang 64 SGK 

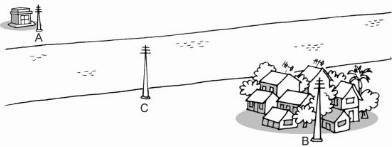
Một trạm biến áp và một khu dân cư được xây dựng cách xa hai bờ sông tại hai địa điểm A và B (h.19).

Hãy tìm trên bờ sông gần khu dân cư một địa điểm C để dụng một cột mắc dây đưa điện từ trạm biến áp về cho khu dân cư sao cho độ dài đường dây dẫn là ngắn nhất.

Lời giải:

Để độ dài đường dây là ngắn nhất thì C nằm trên đoạn thẳng AB, tức là:

AC + BC = AB.

Thật vậy, nếu C nằm ngoài đoạn thẳng AB thì ba điểm A, B, C tạo thành một tam giác ABC. Theo định lý tổng hai cạnh trong tam giác ta có:

AC + BC > AB

Vậy để độ dài đường dây là ngắn nhất thì C nằm trên đoạn thẳng AB.

Giải Bài 22 tập 2 trang 64 SGK Toán lớp 7 

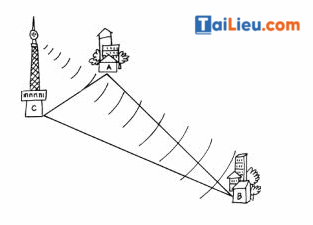
Ba thành phố A, B, C là ba đỉnh của một tam giác; biết rằng: AC = 30km, AB = 90km (h.20).

a) Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B có nhận được tín hiệu không? Vì sao?

b) Cũng câu hỏi như vậy với máy phát sóng có bán kính hoạt động bằng 120km?

Lời giải:

Trong ΔABC ta có:

AB - AC < BC < AB + AC (Bất đẳng thức trong tam giác)

Thay số ta được: 90 - 30 < BC < 90 + 30

hay 60 < BC < 120

a) Vì BC > 60 nên nếu đặt máy phát sóng có bán kính hoạt động bằng 60 km thì B không nhận được tín hiệu.

b) Vì BC < 120 nên nếu đặt máy phát sóng có bán kính hoạt động bằng 120 km thì B có nhận được tín hiệu.

CLICK NGAY vào nút TẢI VỀ dưới đây để tải giải toán lớp 7 trang 61 - 64 file word, pdf hoàn toàn miễn phí