Giải toán lớp 7 trang 81, 82, 83 SGK tập 2 đầy đủ nhất

Giải Toán lớp 7 SGK tập 2 trang 81, 82, 83: Tính chất ba đường cao của tam giác bao gồm đáp án và hướng dẫn giải chi tiết tương ứng với từng bài tập trong sách. Lời giải bài tập Toán 7 này sẽ giúp các em học sinh ôn tập các dạng bài tập có trong sách giáo khoa. Sau đây mời các em cùng tham khảo lời giải chi tiết

Trả lời câu hỏi Toán 7 Tập 2 Bài 9 trang 81 SGK

Dùng eke vẽ 3 đường cao của tam giác ABC.

Hãy cho biết ba đường cao của tam giác đó có cùng đi qua một điểm hay không.

Lời giải

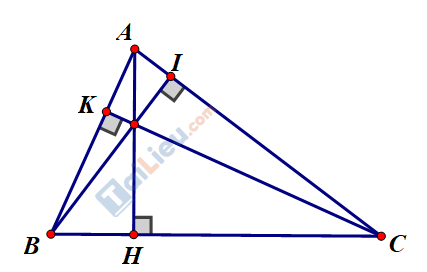
Ta vẽ đường ba đường cao của tam giác ABC như hình vẽ

Ba đường cao đó là: AH, BI, CK

Dựa vào hình vẽ ta thấy ba đường cao của tam giác cùng đi qua một điểm

Trả lời câu hỏi Toán lớp 7 Tập 2 Bài 9 trang 82

Hãy phát biểu và chứng minh các trường hợp còn lại của nhận xét trên (xem như những bài tập).

Lời giải

- Bài tập 1: Nếu một tam giác có một đường trung trực đồng thời là đường phân giác thì tam giác đó là một tam giác cân

Xét ΔABC có AI vừa là đường trung trực vừa là đường phân giác

AI là đường trung trực ⇒ AI ⊥ BC và I là trung điểm BC

Xét hai tam giác vuông ΔABI và ΔACI có:

AI chung

∠(BAI) = ∠(CAI) (do AI là phân giác góc BAC)

⇒ ΔABI = ΔACI (góc nhọn – cạnh góc vuông)

⇒ AB = AC (hai cạnh tương ứng)

⇒ ΔABC cân tại A

- Bài tập 2: Nếu một tam giác có một đường trung trực đồng thời là đường cao thì tam giác đó là một tam giác cân

Xét ΔABC có AI vừa là đường trung trực vừa là đường cao

⇒ AI ⊥ BC và I là trung điểm BC

Xét hai tam giác vuông ΔABI và ΔACI có:

AI chung

IB = IC (do I là trung điểm BC)

⇒ ΔABI = ΔACI (hai cạnh góc vuông)

⇒ AB = AC (hai cạnh tương ứng)

⇒ ΔABC cân tại A

- Bài tập 3: Nếu một tam giác có một đường phân giác đồng thời là đường cao thì tam giác đó là một tam giác cân

Xét ΔABC có AI vừa là đường phân giác vừa là đường cao

AI là đường cao ⇒ AI ⊥ BC

Xét hai tam giác vuông ΔABI và ΔACI có:

AI chung

∠(BAI) = ∠(CAI) (do AI là phân giác góc BAC)

⇒ ΔABI = ΔACI (góc nhọn – cạnh góc vuông)

⇒ AB = AC (hai cạnh tương ứng)

⇒ ΔABC cân tại A

- Bài tập 4: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là một tam giác cân

Xét ΔABC có AI vừa là đường trung tuyến vừa là đường cao

AI là đường cao ⇒ AI ⊥ BC

AI là đường trung tuyến ⇒ I là trung điểm BC

Xét hai tam giác vuông ΔABI và ΔACI có:

AI chung

IB = IC (do I là trung điểm BC)

⇒ ΔABI = ΔACI (hai cạnh góc vuông)

⇒ AB = AC (hai cạnh tương ứng)

⇒ ΔABC cân tại A

Giải Bài 58 trang 83 SGK Toán 7 tập 2

Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.

Lời giải:

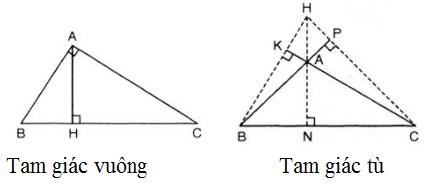
- Trường hợp tam giác vuông:

Xét tam giác ABC vuông tại A thì BA ⊥ CA hay A là giao điểm của hai đường vuông góc trong tam giác => A trực tâm của tam giác.

Vậy trong tam giác vuông thì trực tâm trùng với đỉnh góc vuông.

- Trường hợp tam giác tù:

Giả sử tam giác ABC có góc A tù => BC là cạnh lớn nhất hay BC > BA.

Từ B kẻ đường thẳng BK vuông góc với CA. Ta có: KA, KC lần lượt là hình chiếu của BA, BC.

Vì BC > BA nên KC > KA hay K phải nằm ngoài đoạn thẳng AC. Do đó ta có đường cao BK như hình vẽ.

Tương tự với đường cao CP.

Gọi H là giao điểm của BK và CP => H chính là trực tâm của tam giác. Ta thấy H ở bên ngoài tam giác.

Vậy trực tâm của tam giác tù nằm ở bên ngoài tam giác đó.

Giải Bài 59 trang 83 SGK Toán lớp 7 tập 2

Cho hình 57.

a) Chứng minh NS ⊥ LM

b) Khi góc LNP = 50o, hãy tính góc MSP và góc PSQ.

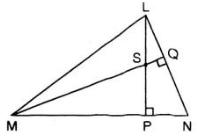
Hình 57

Lời giải:

a) Trong ΔNML có:

LP ⊥ MN nên LP là đường cao

MQ ⊥ NL nên MQ là đường cao

mà PL ∩ MQ = {S}

Suy ra S là trực tâm của tam giác nên đường thẳng SN chứa đường cao từ N hay SN ⊥ ML.

b) ΔNMQ vuông tại Q có

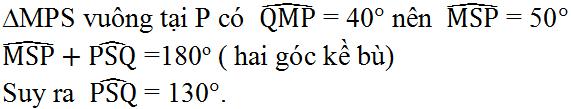
Giải Bài 60 Toán 7 tập 2 trang 83 SGK 

Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K).

Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.

Chứng minh KN ⊥ IM.

Lời giải:

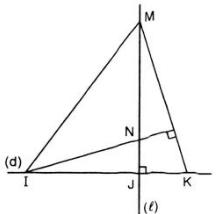
Nối M với I ta được ΔMIK.

Trong ΔMIK có: MJ ⊥ IK (do l ⊥ d) và IN ⊥ MK

Do đó N là trực tâm của ΔMIK.

Suy ra KN là đường cao thứ ba của ΔMIK hay NK ⊥ IM (đpcm).

Giải Toán 7 tập 2 Bài 61 trang 83 SGK

Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.

a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.

b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.

Lời giải:

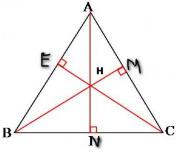
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E.

Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E.

a) ΔHBC có:

HN ⊥ BC nên HN là đường cao

BE ⊥ HC nên BE là đường cao

CM ⊥ BH nên CM là đường cao

Vậy A là trực tâm của ΔHBC.

b) Tương tự, trực tâm của ΔAHB là C; ΔAHC là B.

Giải Bài 62 Toán 7 tập 2 trang 83 SGK

Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.

Lời giải:

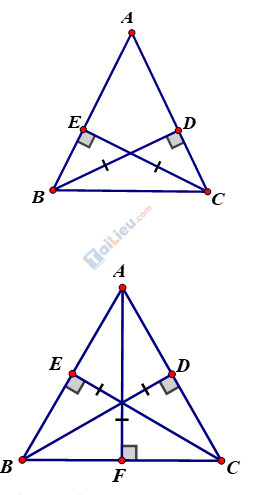
a) Hai đường cao bằng nhau

Vẽ BH ⊥ AC và CK ⊥ AB

Xét hai tam giác vuông KBC và HCB có:

Cạnh BC chung

BH = CK (gt)

a) Hai đường cao bằng nhau

Vẽ BH ⊥ AC và CK ⊥ AB

Xét hai tam giác vuông KBC và HCB có:

Cạnh BC chung

BH = CK (gt)

Vậy ΔABC cân tại A (đpcm).

b) Ba đường cao bằng nhau

Từ a) ta có:

Nếu BH = CK thì ΔABC cân tại A => AB = AC (1)

Nếu AI = BH thì ΔABC cân tại C => CA = CB (2)

Từ (1) và (2) ta có: AB = BC = AC

Vậy ΔABC là tam giác đều.

CLICK NGAY vào nút TẢI VỀ dưới đây để tải Giải toán 7 trang 81, 82, 83 file word, pdf hoàn toàn miễn phí