Giải SBT Toán 11 trang 163, 164, 165 tập 1: Giới hạn của hàm số

Giải SBT Toán 11 bài 2: Giới hạn của hàm số, hy vọng qua bộ tài liệu các bạn học sinh sẽ có kết quả cao hơn trong học tập.

Giải bài 1 SBT Toán 11 trang 163 Đại số và Giải tích

Dùng định nghĩa tìm các giới hạn

a) lim_x→5x+3/x−3

b) lim_x→+∞x³+1/x²+1

Giải:

a) - 4 ; b) + ∞

Giải bài 2 Toán 11 trang 163 Đại số và Giải tích SBT

a) Chứng minh rằng hàm số y=sinx không có giới hạn khi x→+∞

b) Giải thích bằng đồ thị kết luận ở câu a).

Giải:

a) Xét hai dãy số (a_n) với a_n=2nπ và (b_n) với (b_n)=π/2+2nπ(n∈N∗)

Ta có, lima_n=lim2nπ=+∞

limb_n=lim(π/2+2nπ)

=limn(π/2n+2π)=+∞

limsina_n=limsin2nπ=lim0=0

limsinb_n=limsin(π/2+2nπ)=lim1=1

Như vậy, an→+∞,bn→+∞ nhưng limsina_n≠limsinb_n. Do đó, theo định nghĩa, hàm số y=sinx không có giới hạn khi x→+∞

Giải bài 3 Toán 11 trang 163 SBT Đại số và Giải tích

Cho hai hàm số y=f(x) và y=g(x) cùng xác định trên khoảng (−∞,a). Dùng định nghĩa chứng minh rằng, nếu lim_x→−∞f(x)=L và lim_x→−∞g(x)=M thì lim_x→−∞f(x).g(x)=L.M

Giải:

Giả sử (x_n) là dãy số bất kì thoả mãn x_n<ax và x_n→−∞

Vì lim_x→−∞f(x)=L nên lim_n→+∞f(x_n)=L

Vì lim_x→−∞g(x)=M nên lim_n→+∞g(x_n)=M

Do đó, limn_→+∞f(xn).g(xn)=L.M

Từ định nghĩa suy ra lim_x→−∞f(x).g(x)=L.M

Giải bài 4 Toán 11 SBT trang 163 Đại số và Giải tích

Tìm giới hạn của các hàm số sau:

a) f(x)=x²−2x−3/x−1 khi x→3;

b) h(x)=2x³+15/(x+2)² khi x→−2;

c) k(x)= khi x→−∞;

d) f(x)=x³+x²+1 khi x→−∞

e) h(x)=x−15/x+2 khi x→−2+ và khi x→−2−

Giải:

a) 0;

b) −∞;

c) lim_x→−∞

=lim_x→−∞|x|

=lim_x→−∞=+∞

d) lim_x→−∞(x³+x²+1)=lim_x→−∞x³(1+1/x+1/x³)=−∞

e) −∞ và +∞

Giải bài 5 SBT trang 163 Đại số và Giải tích Toán 11

Tính các giới hạn sau:

a) lim_x→−3x+3/x²+2x−3

b) lim_x→0(1+x)³−1/x

c) lim_x→+∞x−1/x²−1

d) lim_x→5x−5/√x−√5

e) lim_x→+∞=x−5/√x+√5

f) lim_x→−2√x2+5−3/x+2

g) lim_x→1√x−1/√x+3−2

h) lim_x→+∞1−2x+3x³/x³−9

i) lim_x→01/x².(1/x²+1.−1)

j) lim_x→−∞(x²−1)(1−2x)⁵/x⁷+x+3

Giải:

a) lim_x→−3x+3/x²+2x−3=lim_x→−3x+3/(x−1)(x+3)=lim_x→−31/x−1=−1/4

b)

lim_x→0(1+x)³−1/x

=lim_x→0(1+x−1)[(1+x)²+(1+x)+1]/x

=lim_x→0x[(1+x)²+(1+x)+1]/x

=lim_x→0[(1+x)²+(1+x)+1]=3

c) lim_x→+∞x−1/x²−1=lim_x→+∞

d) lim_x→5x−5/√x−√5

=lim_x→5(√x−√5)(√x+√5)/√x−√5

=lim_x→5(√x+√5)=2√5

e)

lim_x→+∞x−5/√x+√5

=lim_{x→+∞=+∞}

(Vì 1/√x+√5/x>0 với mọi x>0).

f) lim_x→−2√x2+5−3/x+2

=lim_x→−2x²+5−9/(x+2)(√x²+5+3)

=lim_x→−2(x−2)(x+2)/(x+2)(√x²+5+3)

=lim_x→−2x−2/√x²+5+3=−2/3

g)

lim_x→1√x−1/√x+3−2

=lim_x→1(√x−1)(√x+3+2)/x+3−4

=lim_x→1(√x−1)(√x+3+2)/x−1

=lim_x→1(√x−1)(√x+3+2)/(√x−1)(√x+1)

=lim_x→1√x+3+2/√x+1=2

h) lim_x→+∞1−2x+3x³/x³−9=limx→+∞

i)

lim_x→01/x²(1/x²+1−1)

=lim_x→01/x².(−x²/x²+1)

=lim_x→0−1/x²+1=−1

j)

lim_x→−∞(x²−1)(1−2x)⁵/x⁷+x+3

=lim_x→−∞x²(1−1/x²).x⁵(1/x−2)⁵/x⁷+x+3

=lim_x→−∞(1−1/x²)(1/x−2)⁵/1+1/x⁶+3/x⁷

=(−2)⁵=−32

Giải bài 5 SBT trang 164 Toán 11 Đại số và Giải tích

Tính giới hạn của các hàm số sau khi x→+∞ và khi x→−∞

a) f(x)=

b) f(x)=x+

c) f(x)=

Giải:

a) Khi x→+∞

lim_x→+∞=lim_x→+∞

=lim_x→+∞=lim_x→+∞

Khi x→−∞

x_→−∞/x+2=lim_x→−∞|x|/x+2

=lim_x→−∞−x/x+2=lim_x→−∞

b) Khi x→+∞

lim_x→+∞(x+)

=lim_x→+∞

=lim_x→+∞x=+∞

Khi x→−∞

lim_x→−∞(x+)

=lim_x→−∞

=lim_x→−∞

=lim_x→−∞

=lim_x→−∞

=lim_x→−∞

c) Khi x→+∞

lim_x→+∞()

=lim_x→+∞

=lim_x→+∞

=lim_x→+∞

Khi x→−∞

lim_x→−∞

=lim_x→−∞

=lim_x→−∞

=_{limx→−∞}

Giải bài 6 SBT Toán 11 trang 164 Đại số và Giải tích

Cho hàm số f(x)=2x²−15x+12/x²−5x+4 có đồ thị như hình 4

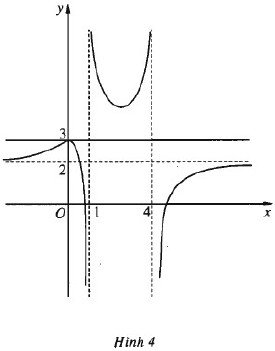
a) Dựa vào đồ thị, dự đoán giới hạn của hàm f(x) số khi x→1⁺;x→1⁻;x→4⁺;x→4⁻;x→+∞;x→−∞

b) Chứng minh dự đoán trên.

Giải:

a) Dự đoán:

lim_x→1+f(x)=+∞;lim_x→1−f(x)=−∞;lim_x→4+f(x)=−∞;

lim_x→4−f(x)=+∞;lim_x→+∞f(x)=2;lim_x→−∞f(x)=2.

b) Ta có

lim_x→1+(2x²−15x+12)=−1<0,lim_x→1+(x²−5x+4)=0

và x²−5x+4<0 với mọi x∈(1;4) nên lim_x→1+2x²−15x+12/x²−5x+4=+∞

Vì

lim_x→1−(2x²−15x+12)=−1<0,

lim_x→1−(x²−5x+4)=0

và x²−5x+4>0 với mọi x < 1 nên lim_x→1−2x²−15x+12/x²−5x+4=−∞

Vì

lim_x→4+(2x²−15x+12)=−16<0,

lim_x→4+(x²−5x+4)=0

và x²−5x+4>0 với mọi x > 4 nên lim_x→4+2x²−15x+12/x²−5x+4=−∞

Vì

lim_x→4−(2x²−15x+12)=−16<0,

lim_x→4−(x²−5x+4)=0

và x²−5x+4<0 với mọi x∈(1;4) nên lim_x→4−2x²−15x+12/x²−5x+4=+∞

lim_x→+∞2x²−15x+12/x²−5x+4=lim_x→+∞ 

lim_x→−∞2x²−15x+12/x²−5x+4=lim_x→−∞

Giải bài 7 SBT Toán 11 Đại số và Giải tích trang 164

Cho hàm số

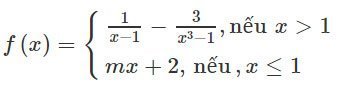
Với giá trị nào của tham số m thì hàm số f(x) có giới hạn khi x→1? Tìm giới hạn này.

Giải:

lim_x→1+f(x)=lim_x→1+(1/x−1−3/x3−1)

=lim_x→1+x²+x−2/(x−1)(x²+x+1)

=lim_x→1+(x−1)(x+2)/(x−1)(x²+x+1)

=lim_x→1+x+2/x²+x+1=1

lim_x→1−f(x)=lim_x→1−(mx+2)=m+2

f(x) có giới hạn khi x→1⇔m+2=1⇔m=−1. Khi đó lim_x→1f(x)=1

Giải bài 8 SBT Toán 11 trang 164 Đại số và Giải tích

Cho khoảng K,x₀∈K và hàm số y=f(x) xác định trên K∖{x₀}

Chứng minh rằng nếu lim_x→x0f(x)=+∞ thì luôn tồn tại ít nhất một số c thuộc K∖{x₀} sao cho f(c)>0

Giải:

Vì lim_x→x0f(x)=+∞ nên với dãy số (x_n) bất kì, x_n∈K∖{x₀} và x_n→x₀ ta luôn có lim_n→+∞f(x_n)=+∞

Từ định nghĩa suy ra f(x_n) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Nếu số dương này là 1 thì f(x_n)>1 kể từ một số hạng nào đó trởđi.

Nói cách khác, luôn tồn tạiít nhất một số x_k∈K∖{x_o} sao cho f(x_k)>1.

Đặt c=x_k ta có f(c)>0

Giải bài 9 Đại số và Giải tích SBT Toán 11 trang 165

Cho hàm số  xác định trên khoảng (a;+∞)

Chứng minh rằng nếu lim_x→+∞f(x)=−∞ thì luôn tồn tại ít nhất một sốc thuộc (a;+∞) sao cho f(c)<0

Giải:

Vì lim_x→+∞f(x)=−∞ nên với dãy số (x_n) bất kì, x_n>a và x_n→+∞ ta luôn có lim_n→+∞f(x)=−∞

Do đó lim_n→+∞[−f(x_n)]=+∞

Theo định nghĩa suy ra −f(x_n) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Nếu số dương này là 2 thì −f(x_n)>2 kể từ một số hạng nàođó trởđi.

Nói cách khác, luôn tồn tại ít nhất một số x_k∈(a;+∞) sao cho −f(x_k)>2 hay f(x_k)<−2<0

Đặt c=x_k ta có f(c)<0

CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn Giải SBT Toán 11 trang 163, 164, 165 file word, pdf hoàn toàn miễn phí.