Giải SBT Toán Hình 11 trang 38 tập 2: Đề toán tổng hợp chương 1

Giải SBT Toán 11 đề toán tổng hợp chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng, với nội dung tài liệu được tổng hợp chi tiết và chính xác sẽ là nguồn thông tin hay để giúp các bạn học sinh học tập tốt hơn môn Toán.

Giải bài 1 SBT Toán Hình 11 trang 38

Trong mặt phẳng Oxy cho đường thẳng d:2x−y+6=0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đối xứng tâm I(−2;1).

Giải:

Dùng công thức tọa độ của phép đối xứng tâm I(−2;1), ta có:

M′=D₁(M)

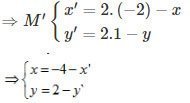
Thế (x;y) vào phương trình d, ta có phương trình

d′:2(−4−x′)−(2−y′)+6=0

⇒d′:2x′−y′+4=0. Đổi kí hiệu, ta có phương trình:

d′:2x−y+4=0

Giải bài 2 Toán Hình 11 trang 38 SBT

Trong mặt phẳng Oxy cho đường tròn (C):x²+y²+2x−4y−11=0. Tìm phép tịnh tiến biến (C) thành (C′):(x−10)²+(y+5)²=16

Giải:

(C) có tâm I(−1;2), bán kính R = 4. (C’) có tâm I′(10;−5), bán kính R’ = 4. Vậy (C′)=Tv^→(C),v^→=II′^→=(11;−7).

Giải bài 3 Toán Hình 11 SBT trang 38

Trong mặt phẳng Oxy cho hai đường thẳng d:x−5y+7=0 và d′:5x−y−13=0. Tìm phép đối xứng qua trục biến d thành d’.

Giải:

Nhận xét d và d’ không song song nên phép đối xứng trục biến d thành d’ có trục là phân giác của góc tạo bởi d và d’. Phương trình các đường phân giác là:

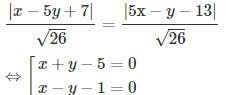
Giải bài 4 Toán SBT Hình 11 trang 38

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−y−3=0. Viết phương trình đường thẳng d₁ là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm I(−1;2) và phép quay tâm O góc quay -90°.

Giải:

Giả sử M₁=D_I(M) và M′=Q_(O;−90⁰)(M₁). Ta có

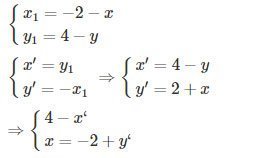
Thế (x;y) theo (x′;y′) vào phương trình d ta có:

3(y′−2)−(4−x′)−3=0

⇔x′+3y′−13=0

⇔x′+3y′−13=0

Vậy phương trình d’ là x+3y−13=0

Giải bài 5 Toán Hình học 11 trang 38 SBT

Trong mặt phẳng Oxy cho đường tròn (C):(x−1)²+(y−2)²=9. Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép đối xứng trục d:x=1

Giải:

Chỉ cần tìm ảnh của tâm đường tròn qua trục d.

Giải bài 6 trang 38 SBT Toán Hình học 11

Trong mặt phẳng Oxy cho đường tròn (C):(x−1)²+(y−2)²=9. Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay Q_(0;−90∘) với O là gốc tọa độ.

Giải:

(C) có tâm I(1;2), bán kính R = 3. Gọi I’; R lần lượt là tâm và bán kính của đường tròn ảnh, ta có:

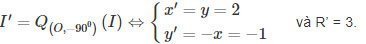
Vậy phương trình (C’) là (x−2)²+(y+1)²=9

Giải bài 7 trang 38 Toán Hình học 11 SBT

Cho tam giác ABC. Trong nửa mặt phẳng có bờ là đường thẳng BC không chứa điểm A, ta dựng hình vuông BCDE. Kẻ DM vuông góc với AB, EN vuông góc với AC, và kẻ đường cao AH của tam giác ABC. Chứng minh rằng ba đường thẳng AD, EN, và AH đồng quy.

Giải:

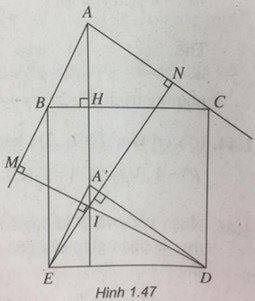
Nếu ta “kéo“ tam giác ABC xuống theo phương AH sao cho B trùng E, C trùng D thì A trùng với A’. Khi đó MD, EN, AH là ba đường cao của tam giác A’ED nên chúng đồng quy.

Thực hiện phép tịnh tiến theo vectơ BE^→ ta có

T_BE^→:A↦A′

B↦E

C↦D

Khi đó, ta có: A′E∥AB,A′D∥AC

Gọi I=DM∩EN

Ta có:

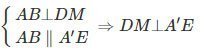
Tương tự, ta có: EN⊥A′D.

Xét ∆A’ED, vì I là giao điểm của hai đường cao nên I là trực tâm của tam giác trên.

Suy ra A′I⊥ED

⇒AI⊥BC′ hay I∈AH

Vậy AH, DM, EN đồng quy tại I.

Giải bài 8 Toán Hình học 11 SBT trang 38

Cho hai đường tròn có cùng bán kính R cắt nhau tại hai điểm M, N. Đường trung trực của MN cắt hai đường tròn tại hai điểm A, B và nằm cùng phía đối với MN. Chứng minh rằng MN²+AB²=4R².

Giải:

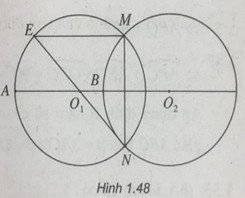
^→:B↦A

M↦E

BA^→=ME^→=O₂O₁^→

∆NME vuông tại M (vì ME∥AB và AB⊥MN), do đó NE là đường kính. Từ đó ta có:

NE²=NM²+ME²

⇔(2R)²=MN²+AB²

⇔MN²+AB²=4R²

Giải bài 9 Toán Hình học 11 trang 38 SBT

Cho đường tròn (O, R) , gọi BC là dây cung cố định của đường tròn và A là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác ABC.

Giải:

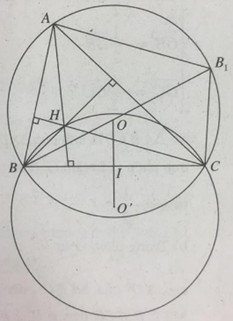
Vẽ đường kính BB1. Vì AB₁∥HC và AH∥B₁C nên AHCB₁ là hình bình hành, suy ra: AH^→=B₁C^→. B, C cố định nên B₁C^→ không đổi.

Như vậy H=T_B1C^→(A). Suy ra tập hợp các điểm H là đường tròn C′(O′;R), chính là ảnh của đường tròn C(O;R) qua phép tịnh tiến T_B1C^→.

+ Xác định tâm của (C’):

Ta có:

O′=T_B1C^→(O),OO′^→=B₁C^→=2OI^→

(I là trung điểm của BC). Vậy O’ đối xứng với O qua BC

Giải bài 10 Toán 11 Hình học trang 38 SBT

Cho tam giác đều ABC và điểm P nằm trong tam giác, sao cho PC = 3, PA = 4 và PB = 5. Tìm chu vi của tam giác ABC.

Giải:

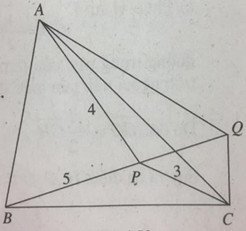
Xét phép quay Q_(C,60⁰):ΔCBP↦ΔCAQ

Ta có:

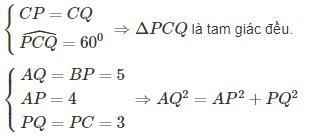
⇒APQ^=90⁰

APC^=APQ^+QPC^=90⁰+60⁰=150⁰

Áp dụng định lí hàm số côsin trong tam giác APC ta tính được chu vi tam giác ABC là: p=3AC=3

CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn Giải SBT Toán Hình 11 trang 38 file word, pdf hoàn toàn miễn phí.