Giải SBT Toán Hình 11 trang 37, 38 tập 2: Ôn tập chương 1

Giải SBT Toán 11 ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng, hy vọng qua bộ tài liệu các bạn học sinh sẽ có kết quả cao hơn trong học tập.

Giải bài 1 SBT Toán Hình 11 trang 37

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−5y+3=0 và vectơ v^→=(2;3). Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến theo vectơ v^→.

Giải:

Gọi M′(x′;y′)∈d′ là ảnh của M(x,y)∈d qua phép tịnh tiến theo vecto v^→(2;3)

Do M(x,y)∈d nên

3x−5y+3=0

⇒3(x′−2)−5(y′−3)+3=0

⇔3x′−5y′+12=0(d′)

Vậy M′(x′;y′)∈d′: 3x′−5y′+12=0

Giải bài 2 Toán SBT Hình 11 trang 37

Cho hình bình hành ABCD có AB cố định, đường chéo AC có độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.

Giải:

Xem D là ảnh của C qua phép tịnh tiến theo vectơ BA^→. Do C chạy trên đường tròn (C) tâm A bán kính m, trừ ra giao điểm của (C) với đường thẳng AB, nên D thuộc đường tròn là ảnh của đường tròn nói trên qua phép tịnh tiến theo vectơ BA^→.

Giải bài 3 Toán Hình 11 SBT trang 37

Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

Giải:

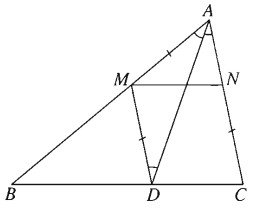
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó MAD^=MDA^=DAC^. Suy ra AD là phân giác trong của góc A. Do đó AD dựng được.Ta lại có NM^→=CD^→, nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ DC^→.

Từ đó suy ra cách dựng:

- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.

- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ CD^→. d cắt AB tại M.

- Dựng N sao cho NM^→=CD^→.

Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.

Giải bài 4 Toán Hình 11 trang 37 SBT

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−2y−6=0

a) Viết phương trình của đường thẳng d₁ là ảnh của d qua phép đối xứng qua trục Oy

b) Viết phương trình của đường thẳng d₂ là ảnh của d qua phép đối xứng qua đường thẳng ∆ có phương trình x+y−2=0.

Giải:

a) d₁:3x+2y+6=0

b) Giao của d và ∆ là A(2;0). Lấy B(0;−3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng ∆ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x−3y−4=0

Giải bài 5 Toán Hình lớp 11 SBT trang 37

Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.

Giải:

Tập hợp các điểm N thuộc đường tròn (C') là ảnh của (C) qua phép đối xứng qua trung điểm của AB.

Giải bài 6 Toán trang 37 Hình học 11 SBT

Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và r, (R>r). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho CD=3AB.

Giải:

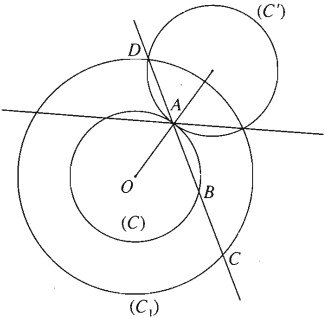
Gọi (C) là đường tròn tâm O bán kính r, (C₁) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và (C₁). Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') với (C₁).

Giải bài 7 Toán Hình học 11 trang 37 SBT

Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y−2=0. Hãy viết phương trình của đường thẳng d’ là ảnh của d qua phép quay tâm O góc 45°.

Giải:

Dễ thấy d chứa điểm H(1;1) và OH⊥d. Gọi H' là ảnh của H qua phép quay tâm O góc 45° thì H′=(0;√2). Từ đó suy ra d' phải qua H' và vuông góc với OH'. Vậy phương trình của d' là y=√2

Giải bài 8 SBT Toán Hình học 11 trang 38

Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng 60°. Chứng minh rằng tứ giác MNPQ là một hình thang cân.

Giải:

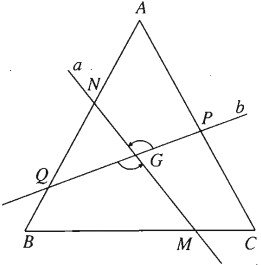
Gọi Q_(G;1200) là phép quay tâm G góc 120⁰. Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.

Tương tự Q_(G;1200) cũng biến Q thành M. Từ đó suy ra GP=GN, GQ=GM. Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì Q_(G;1200) biến PQ thành NM nên PQ=NM. Từ đó suy ra hai tam giác NQM và PMQ bằng nhau. Do đó NQM^=PMQ^. Tương tự QNP^=MPN^.

Từ đó suy ra PNQˆ+NQMˆ=1800

Do đó NP∥QM. Vậy ta có tứ giác MPNQ là hình thang cân.

Giải bài 9 SBT trang 38 Toán Hình học 11

Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng:A′B′^→.A′C′^→=k²AB.^→AC^→

Giải:

Theo định nghĩa của phép đồng dạng ta có B′C′=kBC, từ đó suy ra B′C′²=k²BC². Hay (A'C'^→ - A'B'^→)²=k²(AC^→ - AB^→)²

Suy ra:

A′C′²−2A′C′^→.A′B′^→+A′B′²

=k²(AC²−2AC^→.AB^→+AB²).

Để ý rằng A′C′²=k²AC²,A′B′²=k²AB² ta suy ra điều phải chứng minh.

Giải bài 10 Toán Hình học 11 SBT trang 38

Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng AB^→=pAC^→ nếu  thì trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.

Giải:

Để ý rằng

A′C′²=k²AC²,A′B′²

=k²AB²,A′C′^→.A′B′^→

=k²AC^→.AB^→

Ta có:

(A′B′^→−pA′C′^→)²=A′B′²−2pA′B′^→.A′C′^→+p²A′C′²

=k²(AB²−2pAB^→.AC^→+p²AC²)

=k²(AB^→−pAC^←)²=0

Từ đó suy ra A′B′^→−pA′C′^→=0^→

Giả sử ba điểm A,B,C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó AB^→=tAC^→, với 0<t<1. Áp dụng bài 1.39 ta cũng có A′B→=tA′C′^→, với 0<t<1. Do đó ba điểm A′,B′,C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.

CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn Giải SBT Toán Hình 11 trang 39, 40 file word, pdf hoàn toàn miễn phí.