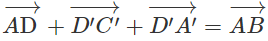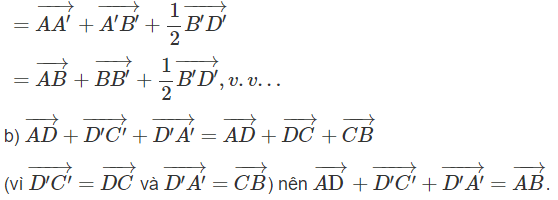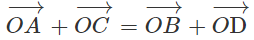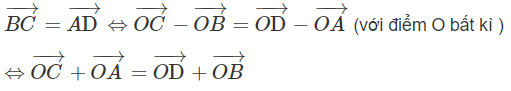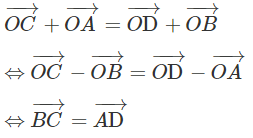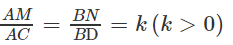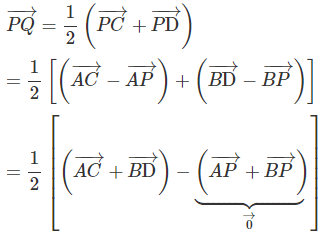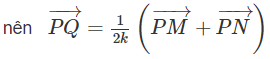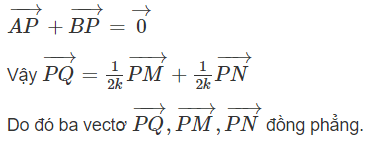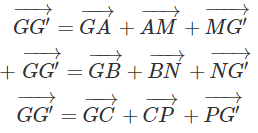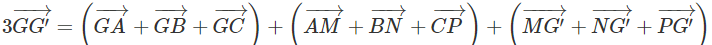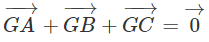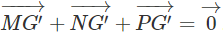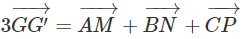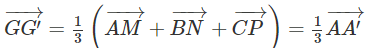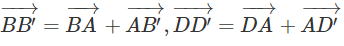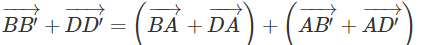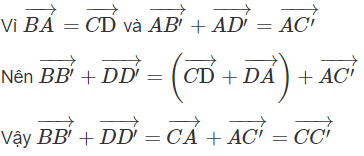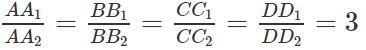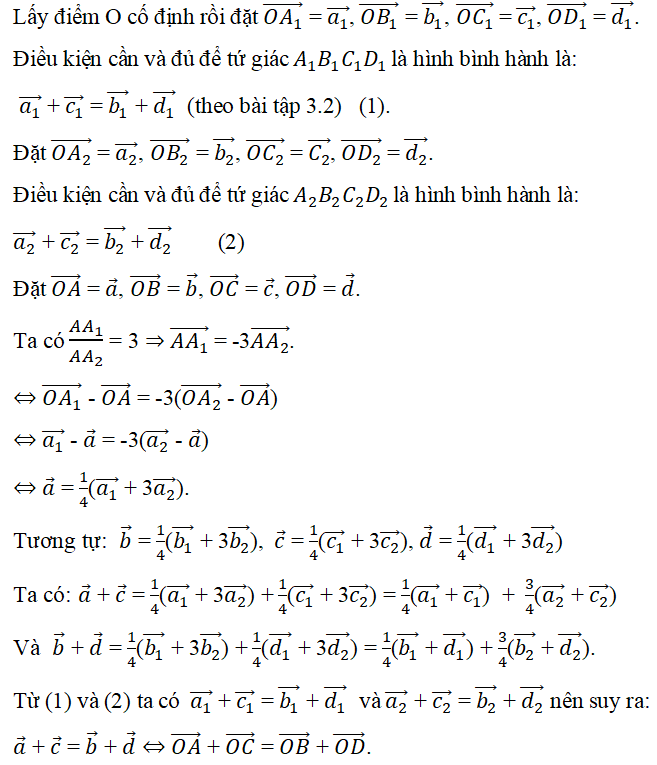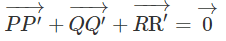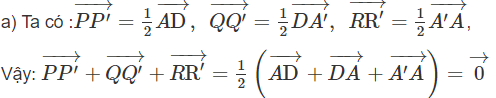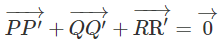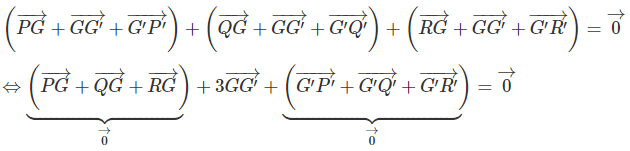Giải SBT Toán Hình 11 trang 129, 130 tập 2: Vectơ trong không gian

Để học tốt Toán lớp 11, dưới đây là các bài giải bài tập Sách bài tập Toán 11 Hình học Bài 1: Vectơ trong không gian.

Giải bài 1 SBT trang 129 Toán Hình 11 

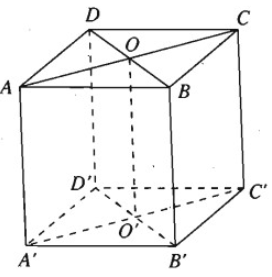
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.

a) Hãy biểu diễn các vectơ AO→, AO'→, theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.

b) Chứng minh rằng 

Lời giải:

 

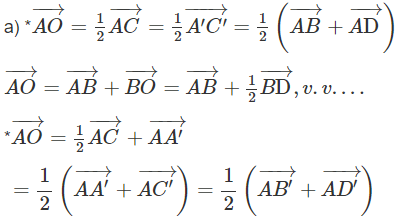
Giải bài 2 trang 129 Toán Hình 11 SBT

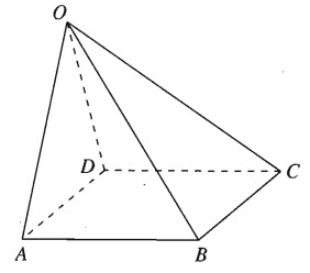
Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là:

Lời giải:

Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:

Ngược lại, giả sử ta có hệ thức:

Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.

Giải bài 3 trang 129 Toán SBT Hình 11

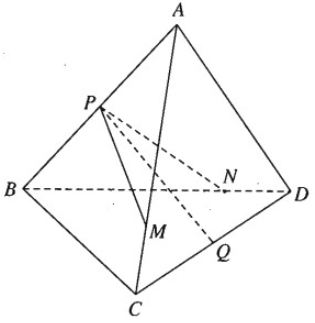
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho

Chứng minh rằng ba vectơ PQ→, PM→, PN→ đồng phẳng.

Lời giải:

Ta có:

   

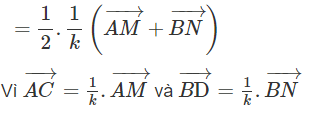
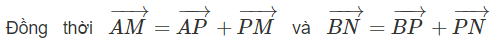
vì

Giải bài 4 trang 130 SBT Toán Hình 11

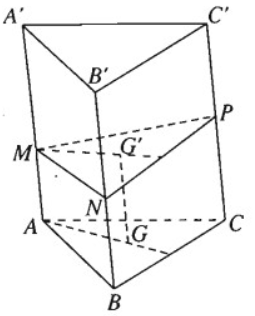
Cho hình lăng trụ tam giác ABC.A'B'C' có độ dài cạnh bên bằng a. Trên các cạnh bên AA', BB', CC' ta lấy tương ứng các điểm M, N, P sao cho AM + BN + CP = a

Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.

Lời giải:

Gọi G và G' lần lượt là trọng tâm của tam giác ABC và tam giác MNP . Ta có:

Cộng từng vế với vế ta có:

Vì G là trọng tâm của tam giác ABC nên 

và G' là trọng tâm của tam giác MNP nên:

Do đó: 

Hay 

Vì điểm G cố định và 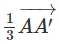 là vectơ không đổi nên G' là điểm cố định. Vậy mặt phẳng (MNP) luôn luôn đi qua điểm G' cố định.

Giải bài 5 SBT Toán Hình 11 trang 130

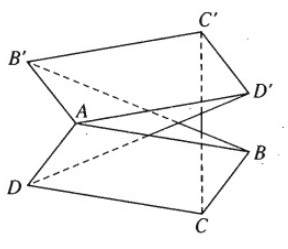
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ BB'→, CC'→, DD'→ đồng phẳng.

Lời giải:

Ta có: 

Do đó: 

Hệ thức 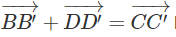 biểu thị sự đồng phẳng của ba vectơ BB'→, CC'→, DD'

Giải bài 6 SBT Toán trang 130 Hình 11

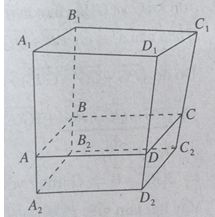
Trên mặt phẳng (α) cho hình bình hành A₁B₁C₁D₁. Về một phía đối với mặt phẳng (α) ta dựng hình bình hành A₂B₂C₂D₂. Trên các đoạn A₁A₂, B₁B₂, C₁C₂, D₁D₂ ta lần lượt lấy các điểm A, B, C, D sao cho

Chứng minh rằng tứ giác ABCD là hình bình hành

Lời giải:

⇔ tứ giác ABCD là hình bình hành.

Giải bài 7 SBT trang 130 Toán Hình 11

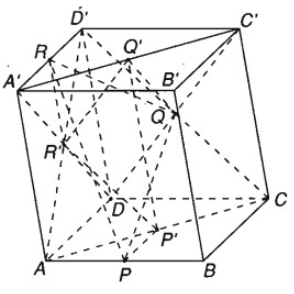
Cho hình hộp ABCD.A'B'C'D' có P và R lần lượt là trung điểm các cạnh AB và A'D'. Gọi P', Q, Q' lần lượt là tâm đối xứng của các hình bình hành ABCD, CDD'C', A'B'C'D', ADD'A'

a) Chứng minh rằng 

b) Chứng minh hai tam giác PQR và P'Q'R' có trọng tâm trùng nhau.

Lời giải:

b) Gọi G và G' lần lượt là trọng tâm các tam giác PQR và P'Q'R'.

Theo câu a) ta có: 

Do đó:

 G trùng với G'

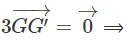
Vậy hai tam giác PQR và P'Q'R' có cùng trọng tâm.

CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn Giải SBT Toán Hình 11 trang 129, 130 file word, pdf hoàn toàn miễn phí.