Giải SBT Toán Hình 11 trang 10 tập 2: Phép biến hình - Phép tịnh tiến

Giải SBT Toán 11 bài 1, 2: Phép biến hình - Phép tịnh tiến, hy vọng qua bộ tài liệu các bạn học sinh sẽ làm bài tập Toán một cách chính xác nhất.

Giải bài 1 SBT Toán Hình học 11 trang 10

Trong mặt phẳng tọa độ Oxy cho v^→=(2;−1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho :

a) A=T_v^→(M)

b) M=T_v^→(A)

Giải:

a) Giả sử A=(x;y). Khi đó

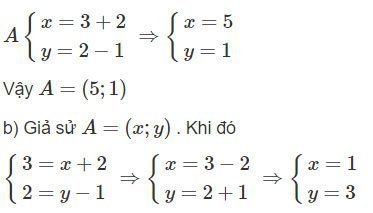
Vậy A=(1;3)

Giải bài 2 Toán Hình học 11 trang 10 SBT

Trong mặt phẳng v^→=(−2;1) cho, đường thẳng d có phương trình 2x−3y+3=0, đường thẳng d₁ có phương trình 2x−3y−5=0

a) Viết phương trình của đường thẳng d’ là ảnh của d qua T_v^→.

b) Tìm tọa độ của w^→ có giá vuông góc với đường thẳng d để d₁ là ảnh của d qua T_w^→.

Giải:

a) Lấy một điểm thuộc d, chẳng hạn M=(0;1).

Khi đó M′=T_v^→(M)=(0−2;1+1)=(−2;2) thuộc d'. Vì d' song song với d nên phương trình của nó có dạng 2x−3y+C=0. Do M′∈d′ nên 2.(−2)−3.2+C=0. Từ đó suy ra C = 10. Do đó d' có phương trình 2x−3y+10=0

b) Lấy một điểm thuộc d, chẳng hạn M=(0;1). Đường thẳng d₂ qua M vuông góc với có vectơ chỉ phương là v^→=(2;−3). Do đó phương trình của d₂ là x−0/2=y−1/−3. Gọi M' là giao của d₁ với d₂ thì tọa độ của nó phải thỏa mãn hệ phương trình:

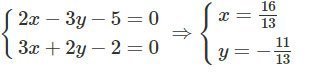
Từ đó suy ra w^→=MM′^→=(16/13;−24/13).

Giải bài 3 Toán Hình học 11 SBT trang 10

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−y−9=0. Tìm phép tịnh tiến theo vectơ có phương song song với trục Ox biến d thành đường thẳng d’ đi qua gốc tọa độ và viết phương trình đường thẳng d’.

Giải:

Giao của d với trục Ox là điểm A(3;0). Phép tịnh tiến phải tìm có vectơ tịnh tiến v^→=AO^→=(−3;0). Đường thẳng d' song song với d và đi qua gốc tọa độ nên nó có phương trình 3x−y=0.

Giải bài 4 Toán SBT Hình học 11 trang 10

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x²+y²−2x+4y−4=0. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ v^→=(−2;5).

Giải:

Cách 1. Dễ thấy (C) là đường tròn tâm I(1;−2), bán kính r=3. Gọi I′=T_v^→(I)=(1−2;−2+5)=(−1;3) và (C') là ảnh của (C) qua T_v^→ thì (C') là đường tròn tâm (I') bán kính r=3. Do đó (C') có phương trình:

(x+1)²+(y−3)²=9

Cách 2. Biểu thức tọa độ của T_v^→ là

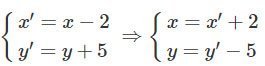
Thay vào phương trình của (C) ta được

(x′+2)²+(y′−5)²−2(x′+2)+4(y′−5)−4=0

⇔x′²+y′²+2x′−6y′+1=0

⇔(x′+1)²+(y′−3)²=9

Do đó (C') có phương trình (x+1)²+(y−3)²=9

Giải bài 5 SBT trang 10 Toán Hình học 11

Cho đoạn thẳng AB và đường tròn (C) tâm O, bán kính r nằm về một phía của đường thẳng AB. Lấy điểm M trên (C), rồi dựng hình bình hành ABMM’. Tìm tập hợp các điểm M’ khi M di động trên (C).

Giải:

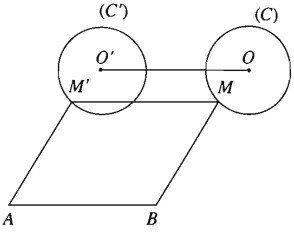
Do tứ giác ABMM’ là hình bình hành nên BA^→=MM′^→ là. Từ đó suy ra M' là ảnh của M qua phép tịnh tiến theo vectơ BA^→. Từ đó suy ra tập hợp các điểm M' là đường tròn (C'), ảnh của C qua phép tịnh tiến theo vectơ BA^→.

CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn Giải SBT Toán Hình 11 trang 10 file word, pdf hoàn toàn miễn phí.