Giải sách bài tập Toán 7 trang 111, 112, 113 tập 1 Định lí đầy đủ

Giải sách bài tập Toán lớp 7 tập 1 trang 111, 112, 113: Định lí bao gồm đáp án và hướng dẫn giải chi tiết tương ứng với từng bài tập trong sách. Lời giải bài tập SBT Toán 7 này sẽ giúp các em học sinh ôn tập các dạng bài tập có trong sách bài tập. Sau đây mời các em cùng tham khảo lời giải chi tiết

Giải Bài 39 trang 111 Sách bài tập Toán 7 Tập 1

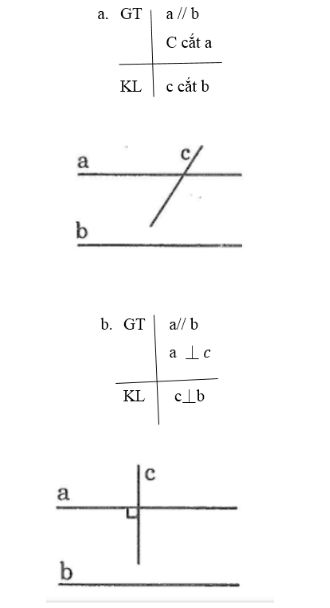
Vẽ hình và viết giả thiết, kết luận của các định lý sau:

a, Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng kia

b, Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.

Lời giải:

Giải Bài 40 Toán 7 Tập 1 trang 112 Sách bài tập 

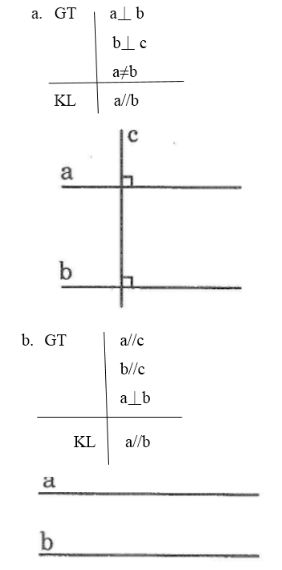
Vẽ hình và viết giả thiết, kết luận của các định lý sau:

a, Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau

b, Hai đường thẳng song song với một đường thẳng thứ ba thì chúng song song với nhau

Lời giải:

Giải Bài 41 trang 112 Sách bài tập Toán lớp 7 Tập 1

Với hai góc kề bù ta có định lý sau:

Hai tia phân giác của hai góc kề bù tạo thành một góc vuông

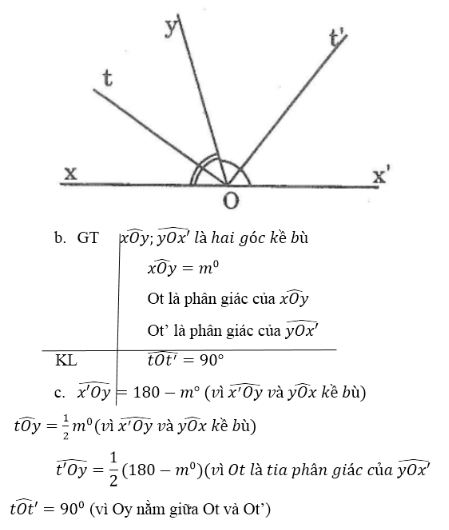
a, Hãy vẽ hai góc xOy và yOx’ kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot’ của góc yOx’ và gọi số đo của góc xOy là m0.

b, Hãy viết giả thiết và kết luận của định lí

c, Hãy điền vào chỗ trống và sắp xếp bốn câu sau đây một cách hợp lí để chứng minh định lí trên.

∠(tOy) =(1/2).m0 vì…

∠(t'Oy) =(1/2 )(180o-m0)vì…

∠(tOt') =90o vì…

∠(x'Oy) =(180o - m0) vì…

Lời giải:

a, Hình vẽ:

Giải Sách bài tập Toán 7 Tập 1 Bài 42 trang 112

Điền vào chỗ trống để chứng minh bài toán sau:

Gọi DI là tia phân giác của góc MND. Gọi EDK là góc đối đỉnh của góc IDM. Chứng minh rằng ⊥(EDK) =⊥(IDN)

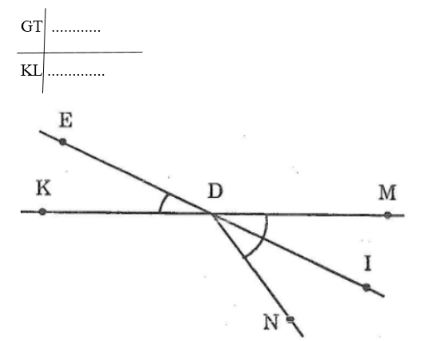
Chừng minh:

∠(IDM) =∠(IDN) (vì…) (1)

∠(IDM) =∠(EDK) (vì…) (2)

Từ (1) và (2) suy ra...

Đó là điều phải chứng minh

Lời giải:

Chứng minh:

∠(IDM) =∠(IDN) (vì DI là tia phân giác của ∠(MDN) (1)

∠(IDM) =∠(EDK) (vì 2 góc đối đỉnh) (2)

Từ (1) và (2) suy ra ∠(EDK) =∠(IDN) (điều phải chứng minh)

Giải Toán 7 Bài 43 trang 112 Sách bài tập Tập 1

Hãy chứng minh định lí:

Nếu một đường thẳng cắt hai đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.

Hướng dẫn: chứng minh tương tự bài tập 30.

Lời giải:

Chứng minh

Giả sử ∠(A1 ) ≠∠(B1 )

Qua B kẻ đường thẳng xy tạo với đường thẳng c có ∠(ABy) =∠(A1)

Theo dấu hiệu của hai đường thẳng song song, ta có xy //a

Vì xy và a tạo ra với đường thẳng c cắt chúng hai góc đồng vị bằng nhau.

Như vậy qua điểm B ở ngoài đường thẳng a kẻ được hai đường thẳng b và xy cùng song song với a. Theo tiên đề Ơ clit thì đường thẳng xy trùng với đường thẳng b. vậy ∠(ABy) ̂ trùng với ∠(B1) nên (A1) = ∠(B1 )

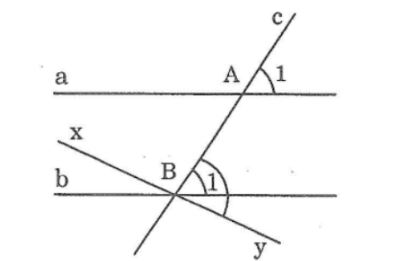
Giải 44 trang 113 Sách bài tập Toán 7 

Chứng minh rằng:

Nếu hai góc nhọn xOy và x’Oy’ có Õ// O’x’; Oy//O’y’ thì ∠(xOy) =∠(x'Oy')

Hướng dẫn: sử dụng tính chất của hai đường thẳng song song (bài 5)

Lời giải:

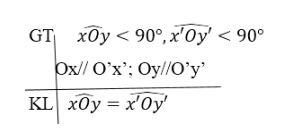
Chứng minh:

Vẽ đường thẳng OO’

Vì Ox // O’x’ nên hai góc đồng vị ∠(O1 ) và ∠(O1 ) bằng nhau

Suy ra: ∠(O1 ) =∠(O')1 (1)

Vì Oy // O’y’ nên hai góc đồng vị ∠(O2 ) và ∠(O')2 bằng nhau

Suy ra: ∠(O2 ) =∠(O')2(2)

Từ (1) và (2) suy ra: ∠(O1 ) - ∠(O')2 =∠(O'1) - ∠(O')2

Vậy ∠(xOy) =∠(x'Oy')

CLICK NGAY vào nút TẢI VỀ dưới đây để tải Giải SBT Toán 7 trang 111, 112, 113 file word, pdf hoàn toàn miễn phí