Giải sách bài tập Toán 7 trang 137, 138, 139 tập 1 đầy đủ

Giải sách bài tập Toán lớp 7 tập 1 trang 137, 138, 139: Tổng ba góc của một tam giác bao gồm đáp án và hướng dẫn giải chi tiết tương ứng với từng bài tập trong sách. Lời giải bài tập SBT Toán 7 này sẽ giúp các em học sinh ôn tập các dạng bài tập có trong sách bài tập. Sau đây mời các em cùng tham khảo lời giải chi tiết

Giải Bài 1 trang 137 Sách bài tập Toán 7 Tập 1

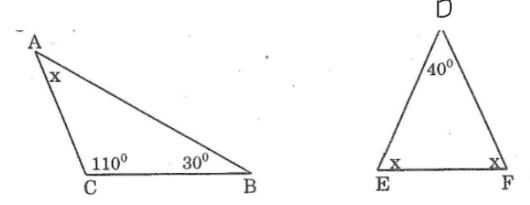
Tính giá trị x ở hình dưới:

Lời giải:

Trong ΔABC ta có:

∠A +∠B +∠C =180o(tổng ba góc trong tam giác)

∠A =180^o-(∠B +∠C)

x=180^o-(30^o+110^o)=40

Trong ΔDEF có:

∠D +∠E +∠F =180^o (tổng ba góc trong tam giác)

Mà ∠E =∠F (gt)

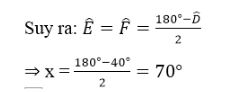
Giải Toán 7 Tập 1 Bài 2 trang 137 Sách bài tập 

Cho tam giác ABC có ∠A =60^o, ∠C =50^o. Tia phân giác của góc B cắt AC ở D. Tính ∠ADB, ∠CDB

Lời giải:

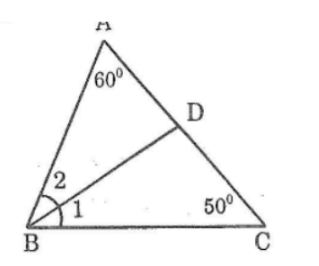
Trong ΔABC ta có:

∠A +∠B +∠C =180^o(tổng ba góc trong tam giác)

⇒∠B =180^o-(∠A +∠C)

⇒x = 180^o-(60^o+50^o) = 70^o

(∠B1) =(∠B2 ) =(1/2 )∠B (vì BD là tia phân giác)

⇒∠B =70^o:2=35^o

Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D

⇒ ∠(ADB) =∠(B1 ) +∠C (tính chất góc ngoài tam giác)

∠(ADB) +∠(BDC) =180^o(hai góc kề bù)

⇒∠(BDC) =180^o-∠(ADB) =180^o-85^o=95^o

Giải Bài 3 trang 137 Sách bài tập Toán lớp 7 Tập 1

Cho tam giác ABC, điểm M nằm trong ta, giác đó. Tia BM cắt AC ở K.

So sánh ∠(AMK) và ∠(ABK)

So sánh ∠(AMC) và ∠(ABC)

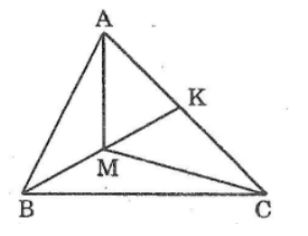
Lời giải:

Trong ΔAMB ta có AMK là góc ngoài tại đỉnh M.

⇒ ∠(AMK) > ∠(ABK) (tính chất góc ngoài tam giác) (1)

Trong ΔCBM ta có KMC là góc ngoài tại đỉnh M

⇒∠(KMC) > ∠(MBC) (tính chất góc ngoài tam giác) (2)

Cộng từng vế (1) và (2) ta có: ∠(AMK) +∠(KMC) > ∠(ABM) +∠(MBC)

Suy ra: ∠(AMC) > ∠(ABC)

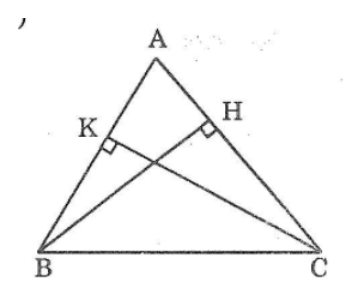
Câu 4: Cho tam giác nhọn ABC. Kẻ BH vuông góc với AC (H thuộc AC), kẻ CK vuông góc với AB (K thuộc AC). Hãy so sánh ∠(ABH) và ∠(ACK)

Lời giải:

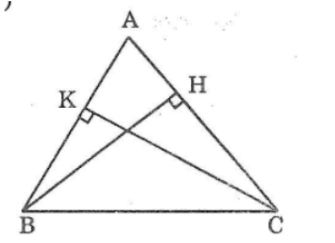
Tam giác nhọn ABH bvuông tại H

⇒ ∠(ABH) +∠A =90^o (tính chất tam giác vuông)

⇒∠(ABH) =90^o - ∠A (1)

Tam giác AC vuông tại K

⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)

⇒∠(ACK) =90^o-∠A (2)

từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)

Giải trang 137 sách bài tập Toán 7 Bài 4 

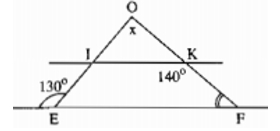
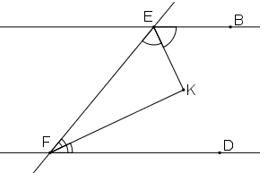
Hãy chọn giá trị đúng của x trong các kết quả A, B, C, D (xem hình dưới , trong đó IK//EF)

A) 100^o

B) 70^o

C) 80^o

D) 90^o

Lời giải:

Ta có: IK //EF suy ra ∠IKF + ∠F = 180^o(hai góc trong cùng phía)

Do đó ∠ F = 180^o - ∠(IKF) =180^o - 140^o = 40^o

Trong ΔOEF ta có góc ngoài tại đỉnh E bằng 130^o nên: ∠ E = ∠ O + ∠ F

suy ra: ∠O = ∠ O + ∠F = 130^o-∠F = 130^o-40^o = 90^o

Vậy chọn đáp án D

Giải Bài 5 trang 137 sách bài tập Toán 7 

Cho tam giác nhọn ABC. Kẻ BH vuông góc với AC ( H thuộc AC), kẻ CK vuông góc với AB ( K thuộc AB). Hãy so sánh ∠(ABH) và ∠(ACK.)

Lời giải:

Tam giác ABH vuông tại H

⇒ ∠(ABH) +∠A =90^o (tính chất tam giác vuông)

⇒∠(ABH) =90^o - ∠A (1)

Tam giác ACK vuông tại K

⇒∠(ACK) +∠A =90^o(tính chất tam giác vuông)

⇒∠(ACK) =90^o-∠A (2)

từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)

Giải Bài 6 trang 137 SBT Toán 7 Tập 1

Cho tam giác ABC có ∠B =∠C =50^o. Gọi Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ rằng Am // BC.

Lời giải:

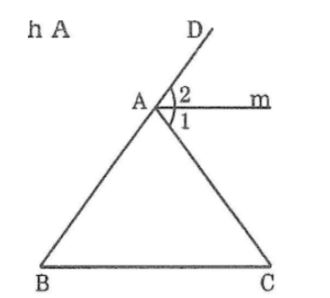
Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A

⇒∠(CAD ) =∠B +∠C =50+50=100^o

(tính chất góc ngoài tam giác)

∠(A1 ) =∠(A2 ) =1/2 ∠(CAD) =50^o (vì tia Am là tia phân giác của ∠(CAD)

Suy ra: ∠(A1) =∠C =50^o

⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

Giải Bài 7 Tập 1 trang 137 Sách bài tập Toán 7

a, Một góc nhọn của eke bằng 30o. Tính góc nhọn còn lại.

b, Một góc nhọn của eke bằng 45o.tính góc nhọn còn lại

Lời giải:

Vì eke là một tam giác vuông , nên:

Một góc nhọn của eke bằng 30o thì góc còn lại bằng:

90^o- 30^o= 60^o

Một góc nhọn của eke bằng 45o thì góc còn lại bằng:

90^o - 45^o= 45^o

Giải Bài 8 Sách bài tập trang 138 Toán 7 Tập 1

Cho tam giác ABC có ∠A =100o,∠B -∠C =20^o. Tính ∠B và∠C

Lời giải:

Trong ΔABC, ta có:

∠A +∠B +∠C =180^o (tổng ba góc trong tam giác)

∠B -∠C =20^o (2)

Từ (1) và (2) suy ra: 2B =100^o⇒B =50^o

Vậy: ∠C =80^o-50^o=30^o

Giải Bài 9 Toán 7 Tập 1 trang 138 Sách bài tập 

Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Tìm góc B.

Lời giải:

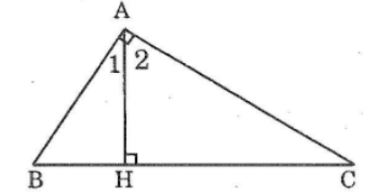
Có thể tìm góc B bằng hia cách:

Cách 1

Ta có: ∠(A1) +∠(A2) =∠(BAC) =90^o (1)

Vì ΔAHB vuông tại H nên:

∠B +∠(A1) =90^o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra ∠B =∠(A2)

Cách 2

Vì ΔABC vuông tại A nên:

∠B +∠C =90^o (theo tính chất tam giác vuông) (1)

Vì ΔAHC vuông tại H nên:

∠(A2) +∠C =90^o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B =∠(A2)

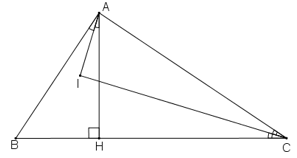
Giải Bài 10 trang 138 sách bài tập Toán 7 

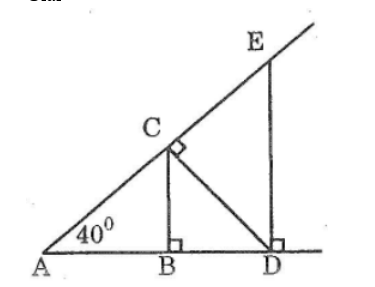
Cho hình dưới:

a. Có bao nhiêu tam giác vuông trong hình?

b. Tính số đo các góc nhọn ở các đỉnh C,D,E

Lời giải:

Có 5 tam giác vuông trong hình:

ΔABC vuông tại B

Δ CDB vuông tại B

Δ EDA vuông tại D

Δ DCA vuông tại C

Δ DCE vuông tại C

ΔABC vuông tại B suy ra:

∠A +∠(ACB) =90^o (theo tính chất tam giác vuông)

⇒ ∠(ACB) =90^o-∠A =90^o-40^o=50^o

∠(ACB) +∠(BCD) =∠(ACD) =90^o

⇒∠(BCD) =90^o-∠(ACB) =90^o-50^o=40^o

ΔACD vuông tại C suy ra:

∠A +∠(CDA) =90^o (theo tính chất tam giác vuông)

⇒ ∠(CDA) =90^o-∠A =90^o-40^o=50^o

∠(CDA) +∠(CDE) =∠(ADE) =90^o

⇒∠(CDE) =90^o-∠(CDA) =90^o-50^o=40^o

ΔDAE vuông tại D suy ra:

∠A +∠E =90^o (theo tính chất tam giác vuông)

⇒∠ E =90^o-∠A =90^o-40^o=50^o

Giải Bài 11 trang 138 SBT Toán 7 Tập 1 

Cho tam giác ABC có ∠B =70^o; ∠C =30^o. Tia phân giác của góc A cắt BC tại D. kẻ AH vuông góc vói BC (H thuộc BC)

Tinh ∠(BAC)

Tính ∠(ADH)

Tính ∠(HAD)

Lời giải:

Trong ΔABC có:

∠(BAC) +∠B +∠C =180^o (tổng ba góc trong tam giác)

Mà ∠(BAC) +70^o+30^o=180

Vậy ∠(BAC) =180^o-70^o-30^o=80^o

Ta có: ∠(A1) =(1/2)∠(BAC) =(1/2).80^o=40^o

(vì Ad tia phân giác của góc BAC)

Trong ΔADC ta có ∠(ADH) là góc ngoài tạ đỉnh D

Do đó: ∠(ADH) =∠(A1) +∠C (tính chất góc ngoài của tam giác)

Vậy ∠(ADH) =40^o+30^o=70^o

ΔADH vuông tại H nên:

∠(HAD) +∠(ADH) =90^o (tính chất tam giác vuông)

⇒∠(HAD) =90^o-∠(ADH)o=90^o-70^o=20^o

Giải Bài 12 trang 138 Toán 7 Tập 1 Sách bài tập 

Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. tính (BIC) ̂biết rằng:

∠B =80^o,∠C =40^o

∠A =80^o

∠A =m^o

Lời giải:

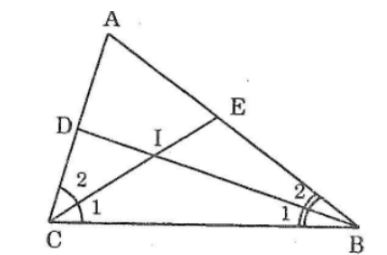
Ta có:

∠(B1) =(1/2)∠(ABC) =(1/2).80^o=40^o (vì BD là tia phân giác ∠(ABC))

∠(C1) =(1/2)∠(ACB) =(1/2).20^o=10^o (vì CE là tia phân giác∠(ACB))

Trong ΔIBC, ta có: ∠(BIC) +∠(B1) +∠(C1) =180o(tổng 3 góc trong tam giác)

Vậy: ∠(BIC) =180o-(∠(B1) +∠(C1))=180^o-(40^o+20^o)=120^o

Ta có:

∠(B1) =(1/2)∠B (vì BD là tia phân giác B)

∠(C1) =(1/2)C (vì CE là tia phân giác∠(C))

Trong ΔABC có:

∠(BIC) +∠(B1) +∠(C1) =180^o (tổng ba goác trong tam giác)

Vậy ∠(BIC) =180^o-((B) +∠(C1))=180^o-(∠B +∠C)/2=180^o-(100^o)/2=130^o

Ta có:∠B +∠C =180^o-m^o

Suy ra: ∠(BIC) =180^o-(180^o-m^o)/2=180-90^o+(m^o)/2=90^o+ (1/2)m^o

Giải Toán lớp 7 Bài 13 trang 138 Sách bài tập Tập 1

Trên hình bên có Ax song sog với By, ∠(CAx) =50^o,∠(CBy) =40^o. Tính ∠(ACB) bằng cách xem nó là góc ngoài của một tam giác.

Lời giải:

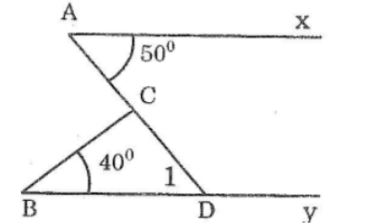
Kéo dài AC cắt By tại D

Vì By // Ax suy ra ∠(D1) =∠A (hai góc so le trong)

Mà ∠A =50^o(gt) nên ∠(D1) =50^o

TrongΔBCD ta có ∠(ACB) là góc ngoài tại đỉnh C

⇒∠(ADC) =∠B +∠(D1) (tính chất góc ngoài của tam giác)

⇒∠(ADC) =40^o+50^o=90^o

Giải Bài 14 trang 138 Tập 1 Sách bài tập Toán 7 

Chứng minh rằng tổng ba goc ngoài ở ba đỉnh của một tam giác thì bằng 360

Lời giải:

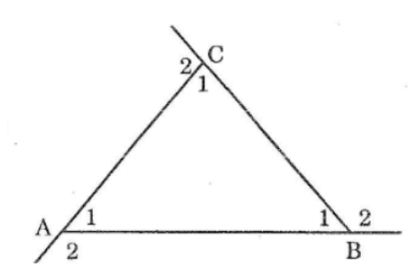
Ta có: ∠(A1) +∠(A2) =180^o(hai goác kề bù)

∠(B1) +∠(B2) =180^o(hai goác kề bù)

∠(C1) +∠(C2)=180^o(hai goác kề bù)

Suy ra: ∠(A1) +∠(A2) +∠(B1) +∠(B2) +∠(C1) +∠(C2) =180.3=540^o

⇒∠(A2) + ∠( B2) +∠(C2) =540^o-(∠(A1) +∠(B1) +∠(C1)) (1)

Trong ΔABC, ta có:

∠(A1) +∠(B1) +∠(C1) =180^o (tổng ba góc trong tam giác) (2)

Từ (1) và (2) suy ra: ∠(A2) +∠(B2) +∠(C2) =540^o-180^o=360^o

Giải SBT trang 138 Bài 15 Toán 7 Tập 1

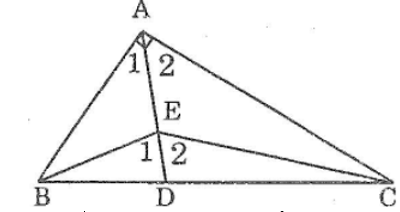
Cho tam giác ABC có ∠A =90^o. Gọi E là điểm nằm trên tam giác đó. Chứng minh rằng góc BEC là góc tù.

Lời giải:

Kéo dài AE cắt BC tại D

Trong ∆ABE ta có ∠E₁ là góc ngoài tại đỉnh E

Suy ra: ∠E₁ > ∠A₁ (tính chất góc ngoài tam giác)(1)

Trong ∆AEC ta có ∠E₂ là góc ngoài tại đỉnh E

Suy ra: ∠E₂ > ∠A₂ (tính chất góc ngoài tam giác)(2)

Cộng từng vế (1) và (2) ta có:

∠E₁ + ∠E₂ > ∠A₁ +∠A₂

Hay ∠ (BEC) > ∠ (BAC) = 90º

Vậy góc (BEC) là góc tù.

Giải Bài 16 trang 139 sách bài tập Toán 7 Tập 1

Cho tam giác ABC có ∠A=90^o, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác của ∠C và ∠BAH cắt nhau ở I. Chứng minh rằng: ∠(AIC)=90^o

Lời giải:

Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H

Trong tam giác vuông AHB ta có: ∠BHA = 90^o

⇒ ∠B + ∠BAH = 90^o (1)

Trong tam giác vuông ABC ta có: ∠BAC = 90^o

⇒ ∠B + ∠C = 90^o (2)

Từ (1) và (2) suy ra: ∠BAH = ∠C (3)

+) Vì AI là tia phân giác của góc BAC nên:

∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)

Do CI là tia phân giác của góc ACB nên:

∠(ACI) = ∠(ICB) = 1/2.∠C (5)

+) Từ (3); (4) và (5) suy ra:

∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)

+) Lại có:

∠BAI + ∠IAC = 90º

Suy ra: ∠ICA + ∠IAC = 90º

Trong ΔAIC có: ∠ICA+ ∠IAC = 90º

Vậy: ∠AIC = 90º.

Giải Bài 17 trang 139 Toán 7 Tập 1 sách bài tập 

Chứng minh rằng nếu một đường thẳng cắt hai đường thẳng song song thì hai tia phân giác của các cặp góc trong cùng phía vuông goác với nhau.

Lời giải:

Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F

Ta có: ∠BEF + ∠EFD = 180^o (hai góc trong cùng phía)

+) Do EK là tia phân giác của góc ∠ BEF nên:

∠E₁ = 1/2 .∠ (BEF) (1)

+) Do FK là tia phân giác của góc EFD nên :

∠F₁ = 1/2 .∠EFD (2)

Từ (1) và (2) suy ra:

∠E₁ +∠F₁ =1/2 .(∠BEF + ∠EFD ) = 1/2 . 180º = 90º ( ∠BEF + ∠EFD = 180º hai góc trong cùng phía)

Trong ΔEKF,ta có:

∠EKF = 180^o-(∠E₁ + ∠F₁) = 180^o-90^o=90^o

Vậy EK ⊥FK

CLICK NGAY vào nút TẢI VỀ dưới đây để tải Giải SBT Toán 7 trang 137, 138, 139 file word, pdf hoàn toàn miễn phí