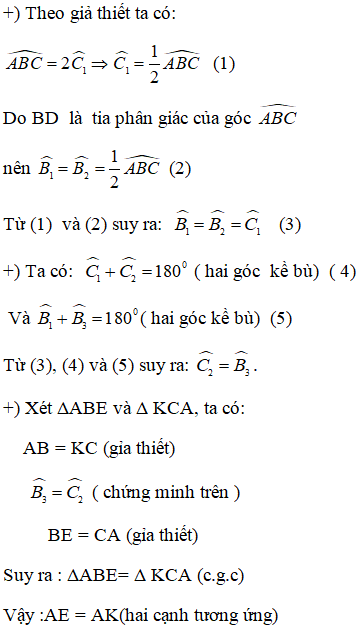Giải sách bài tập Toán 7 trang 142, 143 tập 1 đầy đủ

Hướng dẫn giải sách bài tập Toán lớp 7 trang 142, 143 tập 1: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c) đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài học sắp tới được tốt nhất.

Giải Bài 36 trang 142 Sách bài tập Toán 7 Tập 1

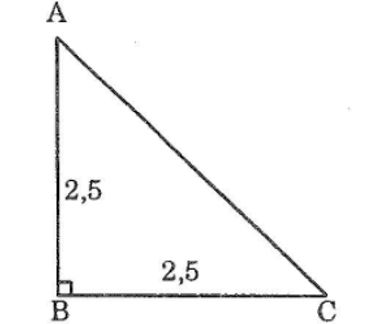
Vẽ tam giác ABC biết BA = Bc = 2,5 cm; ∠B =90o. Sau đó đo các góc A và C để kiểm tra rằng ∠A =∠C =45o

Lời giải:

Ta có: BA = BC = 2,5 cm

Suy ra : ΔABC cân tại B

Vậy: ∠A∠C =(180-∠B )/2=(180-90)/2=45o

Giải Toán 7 Tập 1 Bài 37 trang 142 Sách bài tập 

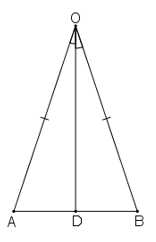
Dựa vào hình dưới, hãy nêu đề toán chứng minh ΔAOC=ΔBOC theo trường hợp cạnh-góc-cạnh.

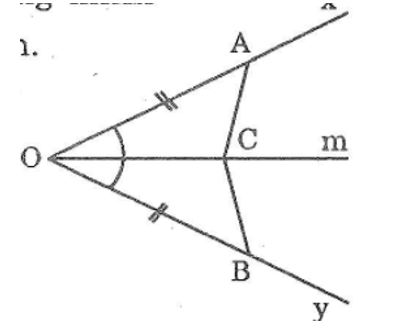
Lời giải:

Cho góc nhọn xOy. Trên tia Ox lấy điểm A trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm C trên tia Om của góc xOy. Chứng minh rằng ΔAOC=ΔBOC

Giải Bài 38 trang 142 Sách bài tập Toán lớp 7 Tập 1

Qua trung điểm I của đoạn thẳng AB, kẻ đường vuông góc với AB, trên đường vuông góc đó lấy hai điểm C và D. nối CA, CB, DA, DB. Tìm các cặp tam giác bằng nhau trong hình vẽ.

Lời giải:

Có hai trường hợp:

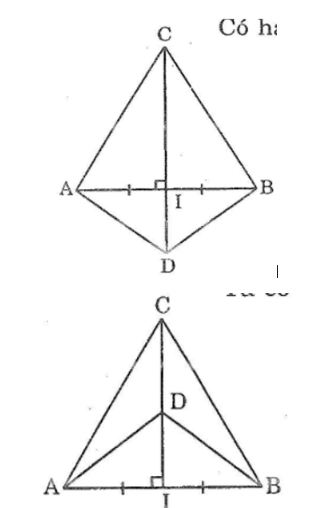
ta có: ΔAIC= ΔBIC(c.g.c)

ΔAID= ΔBID(c.g.c)

ΔACD= ΔBCD(c.c.c)

Giải Sách bài tập Toán 7 Tập 1 Bài 39 trang 142 

Vẽ ΔABC có ∠A= 90o, AB = 3cm, AC = 1cm. Sau đó đo góc C để kiểm tra rằng ∠C ̂≈72o.

Lời giải:

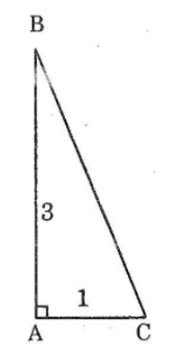
Ta có: ΔABC có ∠A =90o, AB = 3cm, AC = 1cm

Suy ra: ∠C ≈72o.

Giải Bài 40 Tập 1 trang 142 Sách bài tập Toán 7 

Qua trung điểm M của đoạn AB, kẻ đường thẳng vuông góc với AB lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB

Lời giải:

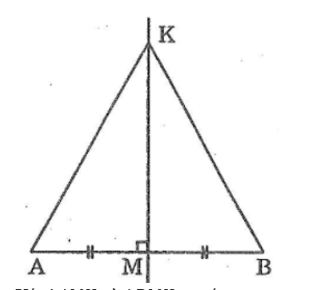
Xét ΔAMK và ΔBMK, ta có:

AM = BM (gt)

∠(AMK) =∠(BMK) =90o (vì KM⊥AB)

Mk cạnh chung

Suy ra: ΔAMK= ΔBMK(c.g.c)

∠(AKM) = ∠(BKM)

Vậy KM là tia phân giác của góc AKB

Giải Bài 41 Sách bài tập trang 142 Toán 7 Tập 1

Hai đoạn thẳng AB và CD căt nhau tại trung điểm O của mối đoạn. Chứng minh rằng AC // BD

Lời giải:

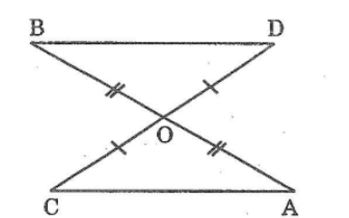
Xét Δ AOC và Δ BOD, ta có:

OA = OB (gt)

∠(AOC) =∠(BOD) ̂(đối đỉnh)

OC=OD

Suy ra: ΔAOC = ΔBOD (c.g.c)

∠A = ∠B ̂(hai góc tương ứng)

Vậy: AC // BD (vì có hai góc so le trong bằng nhau)

Giải Toán 7 Bài 42 trang 142 Sách bài tập Tập 1

Cho tam giác ABC có ∠A =90o. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính số đo góc CDE

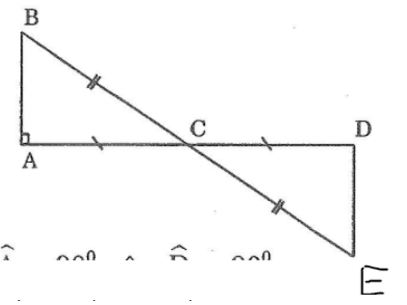
Xét ΔABC và ΔDEC, ta có:

AC = DC (gt)

∠(ACB) =∠(ECD) (đối đỉnh)

BC=EC (gt)

Suy ra: ΔABC= ΔDEC (c.g.c)

=> ∠A = ∠D ̂(hai góc tương ứng). Mà ∠A = 90o nên ∠D =90o

Giải Bài 43 trang 142 SBT Toán 7 Tập 1

Cho tam giác ABC có ∠A =90o, trên cạnh BC lấy điểm E sao cho BE = BA. Trên tia phân giác của góc B cắt AC ở D

a, So sánh các độ dài DA và DE

b, Tính số đo góc BED

Lời giải:

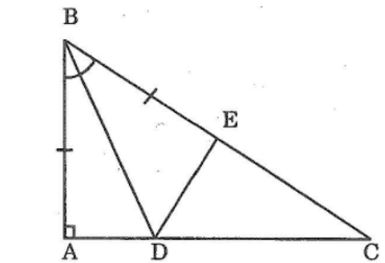
a, Xét ΔABD và ΔEBD, ta có:

AB = BE (gt)

∠(ABD) =∠(DBE) ̂(vì Bd là tia phân giác)

BC cạnh chung

Suy ra: ΔABD và ΔEBD(c.g.c)

⇒ DA = DE (hai cạnh tương ứng)

b, Ta có: ΔABD và ΔEBD(chứng minh trên)

Suy ra: ∠A = ∠(BED) ̂(hai góc tương ứng)

Mà ∠A =90o nên ∠(BED) =90o

Giải Bài 44 trang 143 sách bài tập Toán 7 

Cho tam giác AOB có OA = OB. Tia phân giác của góc O cắt AB ở D. Chứng minh rằng:

a. DA = DB

b. OD ⊥AB

Lời giải:

a, Xét ΔAOD và ΔBOD, ta có:

OA = OB (gt)

∠(AOD) = ∠(BOD)(vì OD là tia phân giác)

OD cạnh chung

Suy ra: ΔAOD= ΔBOD(c.g.c)

Vậy: DA = DB (hai cạnh tương ứng)

b, ΔAOD= ΔBOD (chứng minh trên)

⇒ ∠(ADO) = ∠(BDO) (hai góc tương ứng) (1)

Ta có: ∠(ADO) + ∠(BDO) =180^o(hai góc kề bù) (2)

Từ (1) và (2) suy ra: ∠(ADO) = ∠(BDO) =90^o

Vậy: OD ⊥AB

Giải Toán 7 Tập 1  Bài 45 trang 143 sách bài tập 

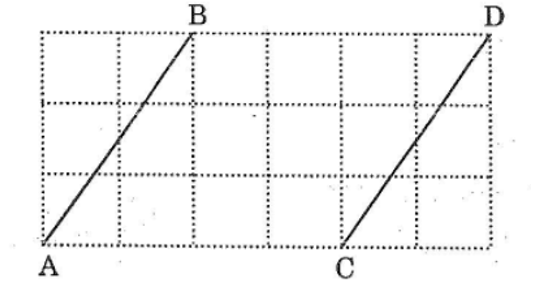
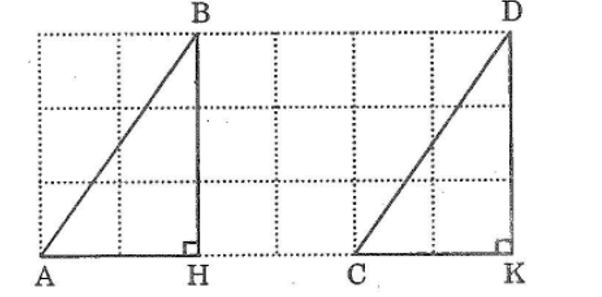
Cho các đoạn thẳng AB và CD trên giấy kẻ ô vuông (hình dưới ). Chứng minh rằng AB = CD, AB // CD

Lời giải:

Gọi giao điểm của đường kẻ ngang đi qua điểm A và đường kẻ dọc đi qua điểm B cắt nhau tại H.

Giao điểm đường kẻ ngang đi qua C và đường kẻ dọc đi qua D là K

Giải Bài 46 sách bài tập Toán 7 trang 143 Tập 1

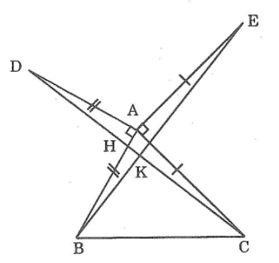
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC).Chứng minh rằng:

a. DC = BE

b. DC ⊥BE

Lời giải:

a, ∠DAC = ∠DAB + ∠BAC = 90^o + ∠BAC

∠BAE = ∠BAC + ∠CAE = ∠BAC + 90^o

⇒ ∠DAC = ∠BAE

Xét ΔABE và ΔADC, ta có:

b, Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K

Ta có: ΔABE = ΔADC (cmt)

⇒ ∠ABE = ∠ADC (hai góc t.ư)

hay ∠HBK = ∠ADH

+ ΔADH và ΔBKH đều có tổng ba góc trong mỗi tam giác bằng 180^o nên có:

∠ADH + ∠DAH + ∠AHD = ∠BKH + ∠KHB + ∠HBK

Mà ∠AHD = ∠BHK (hai góc đối đỉnh)

∠ADH = ∠HBK (chứng minh trên)

Suy ra ∠DAH = ∠HKB

Mà ∠DAH = 90^o nên ∠HKB = 90^o

⇒ DC ⊥ BE (điều phải chứng minh)

Giải Bài 47 trang 143 sách bài tập Toán 7 Tập 1

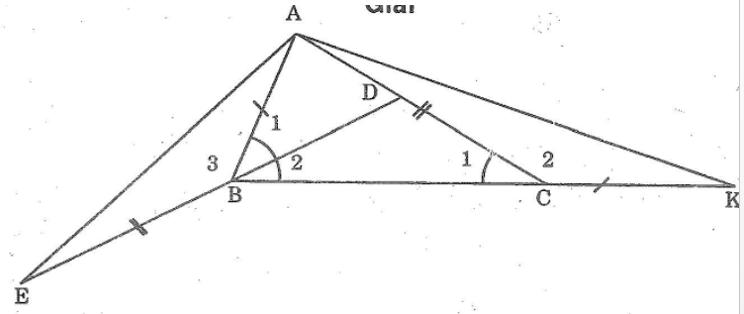
Cho tam giác ABC có ∠B =2∠C . Tia phân giác của góc B cắt AC ở D. trên tia đối của tia BD lấy điểm E sao cho BE = AC. Trên tia đối của tia CB lấy điểm K sao cho CK = AB. Chứng minh rằng AE = AK.

Lời giải:

Giải Bài 48 trang 143 Toán 7 sách bài tập

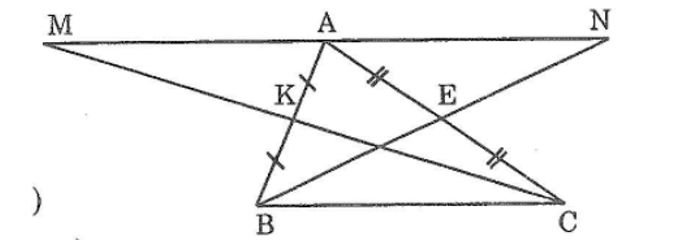
Cho tam giác ABC, K là trung điểm của AB, E là trung điểm của AC. Trên tia đối của tia KC lấy điểm M sao cho KM = KC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng A là trung điểm của MN

Lời giải:

Xét ΔAKM và ΔBKC ta có:

AK = BK (Vì K là trung điểm AB)

∠(AKM) =∠(BKC) (đối đỉnh)

KM=KC (giả thiết)

Suy ra: ΔAKM = ΔBKC(c.g.c)

⇒AM =BC (hai cạnh tương ứng)

Và ∠(AMK) =∠(BCK) (2 góc tương ứng)

Suy ra: AM // BC ( vì có cặp góc so le trong bằng nhau)

Tương tự: ΔAEN= ΔCEB(c.g.c)

⇒ AN = BC (2 cạnh tương ứng)

Và ∠(EAN) =∠(ECB) (2 góc tương ứng)

Suy ra: AN // BC (vì có cặp góc so le trong bằng nhau)

Ta có: AM // BC và AN // BC nên hai đường thẳng AM và AN trùng nhau hay A,M,N thẳng hàng (1)

Lại có: AM = AN ( vì cùng bằng BC) (2)

Từ (1) và (2) suy ra: A là trung điểm của MN

Xét ΔAHB và ΔCKD, ta có:

AH = CK (bằng 2 ô vuông)

∠(AHB) =∠(CKD) =90^o

BH = DK (bằng 3 ô vuông)

Suy ra ΔAHB= ΔCKD (c.g.c)

⇒ AB = CD (hai cạnh tương ứng) và ∠(BAH) =∠(DCK) (hai góc tương ứng)

Hai đường thẳng AB Và CD cắt đường thẳng AK có 2 góc ∠(BAH) và ∠(DCK) ̂ở vị trí đồng vị bằng nhau nên AB // CD.

CLICK NGAY vào nút TẢI VỀ dưới đây để tải Giải SBT Toán 7 trang 142, 143 file word, pdf hoàn toàn miễn phí