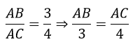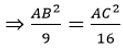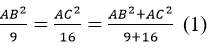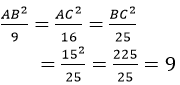Giải sách bài tập Toán 7 trang 152, 153 tập 1 đầy đủ

Hướng dẫn giải sách bài tập Toán lớp 7 trang 152, 153 tập 1: Ôn tập chương 2 đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài học sắp tới được tốt nhất.

Giải Bài 103 trang 152 Sách bài tập Toán 7 Tập 1

Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. Chứng minh rằng CD là đường trung trực của AB.

Lời giải:

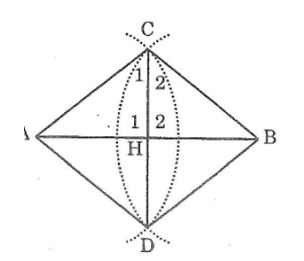
Gọi H là giao điểm của AB và CD

Nối AC, AD, BC, BD

Xét ΔACD và ΔBCD, ta có:

AC = BC (bán kính hai cung tròn bằng nhau)

AD = BD

CD cạnh chung

Suy ra: ΔACD= ΔBCD (c.c.c)

Suy ra: ∠C2 =∠C2 ̂(hai góc tương ứng)

Xét hai tam giác AHC và BHC. Ta có:

AC = BC (bán kính hai cung tròn bằng nhau)

∠C2 =∠C2 (chứng minh trên)

CH cạnh chung

Suy ra: ΔAHC= ΔBHC(c.g.c)

Suy ra: AH = BH (hai cạnh tương ứng) (1)

Ta có: ∠H1 =∠H2 (hai góc tương ứng)

∠H1 + ∠H2 =180° (hai góc kề bù)

Suy ra: ∠H1 =∠H2 =90° => CD ⊥ AB (2)

Từ (1) và (2) suy ra CD là đường trung trực của AB

Giải Bài 104 trang 152 Sách bài tập Toán lớp 7 Tập 1

Cho tam giác ADE cân tại A. Trên cạnh DE lấy các điểm B và C sao cho DB = EC =1/2 DE

a, Tam giác ABC là tam giác gì? Chứng minh điều đó?

b, Kẻ BM ⊥AD, kẻ CN⊥AE. Chứng minh rằng BM = CN

c, Gọi I là giao điểm của MB và NC. Tam giác IBC là tam giác gì? Chứng minh điều đó?

d, Chứng minh rằng AI là tia phân giác của góc BAC

Lời giải:

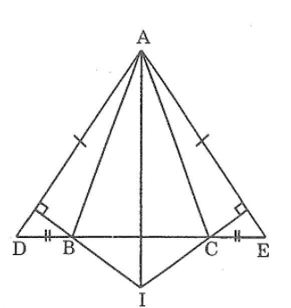
ΔADE cân tại A nên ∠D =∠E

Xét ΔABD và ΔACE, ta có:

AD = AE (gt)

∠D =∠E (chứng minh trên)

DB=EC (gt)

Suy ra: ΔABD= ΔACE (c.g.c)

Suy ra: AB = AC (hai cạnh tương ứng)

Vậy: ΔABC cân tại A

Xét hai tam giác vuông BMD và CNE, ta có:

(BMD) =(CNE) =90o

BD = CE (gt)

∠D =∠E (chứng minh trên)

Suy ra: ΔBMD= ΔCNE (cạnh huyền, góc nhọn)

Ta có: ΔBMD=ΔCNE (chứng minh trên)

Suy ra: ∠DBM =∠ECN (hai góc tương ứng)

∠DBM =∠IBC (đối đỉnh)

∠ECN =∠ICB (đối đỉnh)

Suy ra: ∠IBC =∠ICB hay ΔIBC cân tại I

Xét ΔABI và ΔACI, ta có:

AB = AC (chứng minh trên)

IB = IC (vì ΔIBC cân tại I)

AI cạnh chung

Suy ra: ΔABI= ΔAC I (c.c.c) =>∠BAI =∠CAI ̂(hai góc tương ứng)

Vậy AI là tia phân giác của góc ∠BAC

Giải Toán 7 Tập 1 Bài 105 trang 153 Sách bài tập 

Cho hình dưới trong đó AE ⊥BC. Tính AB biết AE = 4m; AC = 5m; BC = 9m

Lời giải:

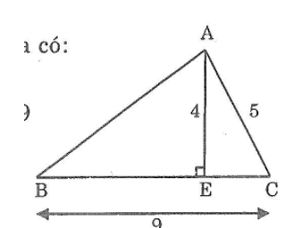
Áp dụng định lý pitago vào tam giác vuông AEC ta có:

AC2=AE2+EC2

=>EC2=AC2-AE2=52-42=25-16=9

=>EC=3M

Ta có: BC = BE + EC

BE = BC – EC = 9 – 3 = 6(m)

Áp dụng định lí pitago vào tam giác vuông AEB, ta có:

AB2=AE2+EB2=42+62=16+36=52

Suy ra: AB = √52(m) ≈7,2m

Giải Sách bài tập Toán 7 Tập 1 Bài 106 trang 153 

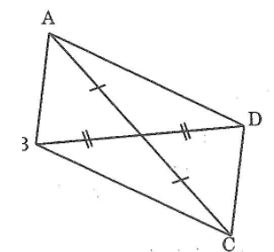
Tìm các tam giác bằng nhau trong hình bên

Lời giải

Ta có: ΔACB=ΔECD (c.g.c)

ΔABD=ΔEDB(c.c.c)

ΔABE=ΔEDA (c.c.c)

Giải Bài 107 Sách bài tập Toán 7 trang 153 Tập 1

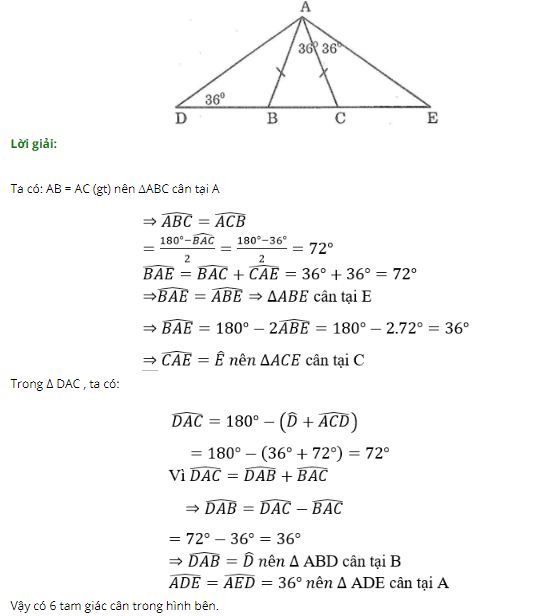
Tìm các tam giác cân trên hình dưới

Giải Bài 108 Toán lớp 7 Tập 1 trang 153 sách bài tập

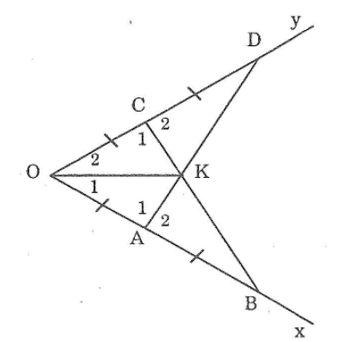
Bạn Mai vẽ tia phân giác của một góc như sau: đánh dấu trên hai cạnh của bốn góc bốn đoạn thẳng bằng nhau: OA = AB = OC = CD (hình dưới). Kẻ các đoạn AD, BC chúng cắt nhau ở K. Hãy giải thích vì sao OK là tia phân giác của góc O.

Hướng dẫn: chứng minh rằng:

a. ΔOAD=ΔOCB

b. ΔKAB=ΔKCD

Lời giải:

+) Ta có: OC = OA; CD = AB nên:

OC + CD = OA + AB hay OD = OB.

+) Xét ΔOAD và ΔOCB. Ta có:

OA = OC (gt)

∠O chung

OD = OB (chứng minh trên )

Suy ra: ΔOAD= ΔOCB (c.g.c)

Suy ra: ∠D = ∠B(hai góc tương ứng)

Và ∠C₁ =∠A₁ (hai góc tương ứng)

Lại có: ∠C₁+∠C₂ =180°(hai góc kề bù)

Và ∠A₁+∠A₂=180°(hai góc kề bù)

Suy ra: ∠C₂ =∠A₂

Xét ΔKCD và ΔKAB, ta có:

∠B = ∠D (chứng minh trên )

CD=AB (gt)

∠C₂ =∠A₂ (chứng minh trên)

suy ra: ΔKCD= ΔKAB,(g.c.g)

=>KC=KA (hai cạnh tương ứng)

Xét ΔOCK và ΔOAK, ta có:

OC = OA (gt)

OK chung

KC = KA (chứng minh trên)

Suy ra: ΔOCK = ΔOAK (c.c.c)

=> ∠O₁=∠O₂̂(hai góc tương ứng)

Vậy OK là tia phân giác góc O

Giải Bài 109 Tập 1 trang 153 sách bài tập Toán 7 

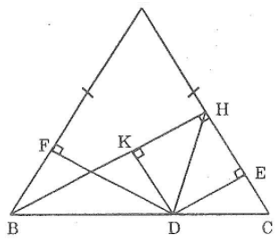
Cho tam giác ABC cân tại A, kẻ BH ⊥ AC. Gọi D là một điểm thuộc cạnh đáy BC. Kẻ DE ⊥ AC, DF ⊥ AB.

Chứng minh rằng DE + DF = BH

Lời giải:

Kẻ DK ⊥ BH

Ta có: BH ⊥AC(gt)

Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)

⇒ ∠KDB = ∠C (hai góc đồng vị)

VìΔABC cân tại A nên ∠B = ∠C (tính chất tam giác cân)

Suy ra: ∠KDB = ∠B

Xét hai tam giác vuông BFD và DKB, ta có:

∠BFD = ∠DKB = 90^o

BD cạnh huyền chung

∠FBD = ∠KDB (chứng minh trên)

Suy ra:ΔBFD=ΔDKB (cạnh huyền góc nhọn)

⇒ DF = BK (hai cạnh tương ứng)(1)

Nối DH. Xét ΔDEH và ΔHKD, ta có:

∠DEH = ∠DKH = 90^o

DH cạnh huyền chung

∠EHD = ∠KDH (hai góc so le trong)

Suy ra:ΔDEH = ΔDKH( cạnh huyền , góc nhọn)

Suy ra: DE = HK ( hai cạnh tương ứng) (2)

Mặt khác: BH = BK + KH (3)

Từ (1), (2) và (3) suy ra: DF + DE = BH

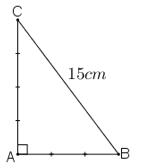
Giải Bài 110 trang 153 sách bài tập Toán 7 

Cho tam giác ABC vuông tại A có AB/AC = 3/4 và BC = 15cm. Tính độ dài AB, AC

Lời giải:

Theo đề bài ta có:

Theo tính chất dãy tỉ số bằng mhau ta có:

tam giác ABC vuông tại A

Áp dụng định lí pitago vào tam giác ABC ta có:

BC² = AB² + AC² (2)

Từ (1) và (2) suy ra:

AB² = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)

AC² = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)

CLICK NGAY vào nút TẢI VỀ dưới đây đê tải Giải SBT Toán 7 trang 152, 153  file word, pdf hoàn toàn miễn phí