Giải sách bài tập Toán 7 trang 147, 148 tập 1 đầy đủ

Giải sách bài tập Toán lớp 7 tập 1 trang 147, 148: Tam giác cân bao gồm đáp án và hướng dẫn giải chi tiết tương ứng với từng bài tập trong sách. Lời giải bài tập SBT Toán 7 này sẽ giúp các em học sinh ôn tập các dạng bài tập có trong sách bài tập. Sau đây mời các em cùng tham khảo lời giải chi tiết

Giải Bài 67 trang 147 Sách bài tập Toán 7 Tập 1

a, Tính góc ở đáy của một tam giác cân biết góc ở đỉnh bằng 50o, bằng ao.

b, Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng 50o, bằng ao

Lời giải:

Vì tam giác cân có hai gốc ở đáy bằng nhau nên số đo của mỗi góc bằng 180o trừ góc ở đỉnh rồi chia cho 2.

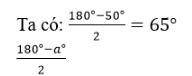
Vì tam giác cân có hai góc ở đáy bằng nhau nên góc ở đỉnh bằng 180o trừ đi hai lần góc ở đáy.

Ta có: 180o-50o.2=180o-100o=80o

180o-a.2

Giải Toán 7 Tập 1 Bài 68 trang 147 Sách bài tập

Cho tam giác ABC cân tại A có ∠A= 100°. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Chứng minh rằng MN // BC

Lời giải:

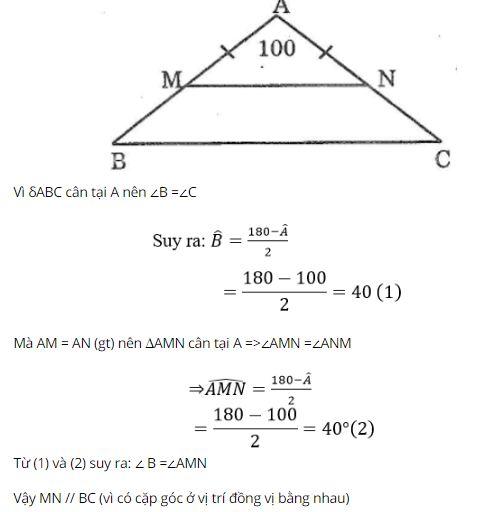
Giải Bài 69 trang 147 Sách bài tập Toán lớp 7 Tập 1

Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB. Chứng minh rằng BM = CN

Lời giải:

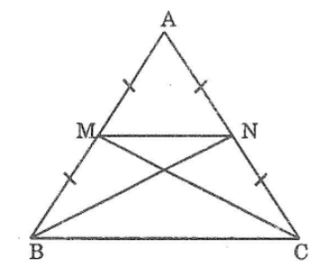
Xét ΔABM và ΔCAN, ta có:

AB = AC (gt)

∠A chung

AM=AN (cùng bằng một nửa AB, AC)

Suy ra: ΔABM = ΔCAN(c.g.c)

Vậy DM = CN ( hai cạnh tương ứng)

Giải Sách bài tập Toán 7 Tập 1 Bài 70 trang 147 

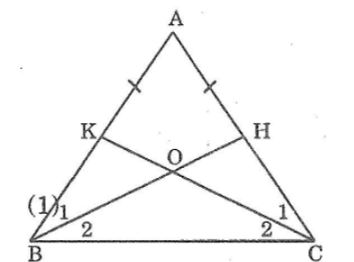
Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK.

Chứng minh rằng ΔOBClà tam giác cân.

Lời giải

Xét ΔABH và ΔACK, ta có:

AB = AC (gt)

A chung

AH=AK (gt)

Suy ra: ΔABH= ΔACK(c.g.c)

⇒B1 =C1 (hai góc tương ứng)

∠ABC= B1 +B29(2)

∠ACB=C1+C2 (3)

∠ABC=∠ACB (tính chất tam giác cân) (4)

Từ (1),(2),(3) và (4) suy ra: B2=C2 hay BOC cân tại O

 

Giải Bài 71 Sách bài tập Toán 7 trang 147 Tập 1

Vẽ lại hình bên vào vở rồi đặt bài toán vẽ tam giác để có hình bên.

Lời giải:

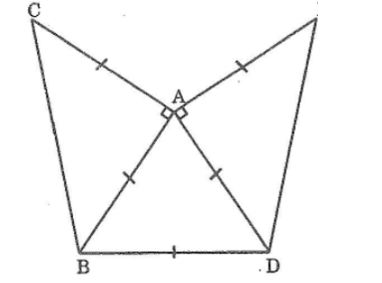
- Vẽ tam giác ABC vuông tại A

- Vẽ tam giác đều ABD sao cho D và C nằm trên 2 nửa mặt phẳng đối nhau có bờ chứa đường thẳng AB.

- Vẽ tam giác vuông cân ADE sao cho E và B nằm trên 2 nửa mặt phẳng đối bờ chứa đường thẳng AD.

Giải Bài 72 trang 147 Tập 1 Sách bài tập Toán 7

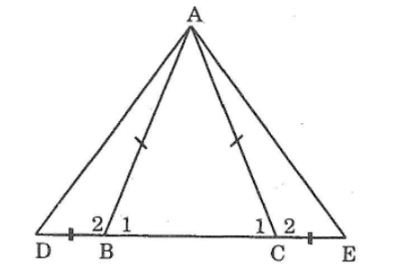
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng ΔADE là tam giác cân.

Lời giải:

Ta có: ΔABC cân tại A

Suy ra:B1=C1 (tính chất tam giác cân)

Lại có:B1 +B2 =180o (kề bù)

C1 +C1 =180o (kề bù)

Suy ra: C1 =B1

Xét ΔABD và ΔACE, ta có:

AB = AC (gt)

C1 =B2 (chứng minh trên)

BD=CE (gt)

Suy ra: ΔABD=ΔACE(c.g.c)

⇒AD=AE (hai cạnh tương ứng)

Vậy ΔADE cân tại A (theo định nghĩa tam giác cân)

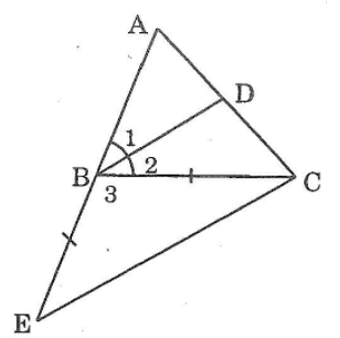
Giải Bài 73 trang 147 sách bài tập Toán 7 

Cho tam giác ABC. Tia phân giác của góc B cắt AC ở D. trên tia đối của tia BA lấy E sao cho BE = BC. Chứng minh rằng BD // EC

Lời giải:

Ta có: BD là tia phân giác của ∠ABC (giả thiết)

Suy ra: 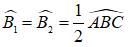 (1)

Lại có: BE = BC (giả thiết)

=>∆BEC cân tại B (theo định nghĩa)

Suy ra: ∠E= ∠BCE (tính chất tam giác cân)

∆BEC có ABC là góc ngoài đỉnh B

=>∠ABC= ∠E + ∠BCE (tính chất góc ngoài tam giác)

Suy ra: ∠ABC=2∠E

Hay ∠E = (1/2)∠ABC (2)

Từ (1) và (2) suy ra: ∠E = ∠B₁ = (1/2)∠ABC

Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)

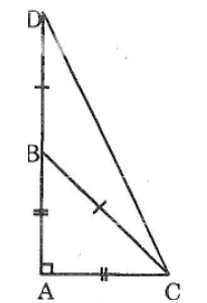
Giải Bài 74 trang 147 sách bài tập Toán lớp 7 Tập 1

Tính số đo các góc của tam giác ACD như hình bên.

Lời giải:

Ta có: ∆ABC vuông cân tại A

Suy ra: ∠ACB=∠ABC=45^o

Lại có: ∆BCD vuông cân tại B (BC = BD)

Suy ra: ∠BCD=∠Dtính chất tam giác cân)

Trong ∆BCD ta có ∠ABC góc ngoài tại đỉnh B

Do vậy: ∠ABC=∠BCD + ∠D (tính chất góc ngoài của tam giác)

Suy ra: ∠ABC= ∠2∠BCD

Do đó: ∠BCD = 1/2 . ∠ABC = 1/2. 45º= 22º30’

=> ∠ACD = ∠ACB + ∠BCD = 45^o+22^o30'=67^o30'

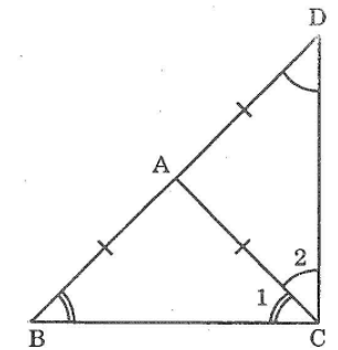
Giải sách bài tập Bài 75 trang 147 Toán 7 Tập 1

Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD

Lời giải:

Ta có: ∆ABC cân tại A

⇒ AB = AC và ∠B = ∠C₁ (tính chất tam giác cân) (1)

Lại có: AD = AB ( do A là trung điểm BD).

Suy ra: AD = AC do đó ∆ACD cân tại A

Nên ∠D =∠C₂(tính chất tam giác cân) (2)

Mà ∠BCD =∠C₁+ ∠C₂ (3)

Từ (1); (2) và (3) suy ra: ∠BCD =∠B +∠D (4)

Trong ∆BCD, ta có:

∠BCD +∠B +∠D =180^o (tổng 3 góc trong tam giác) (5)

từ (4) và (5) suy ra : 2 ∠BCD =180° hay∠BCD =90°

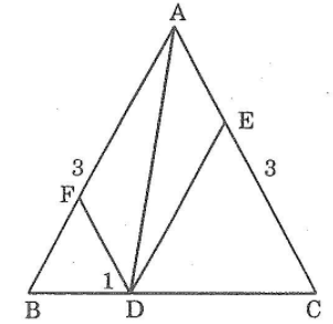
Giải Bài 76 Toán 7 trang 147 sách bài tập Tập 1

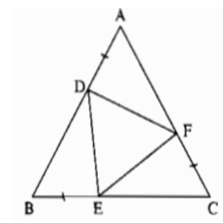
Cho tam giác ABC cân tại A có cạnh bên bằng 3cm. Gọi D là một điểm thuộc đáy BC. Qua D, kẻ cac đường thẳng song song vói các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E.

Tính tổng DE + DF

Lời giải:

Ta có: DF // AC(gt)

=> ∠D₁ = ∠C (hai góc đồng vị) (1)

Lại có: ΔABC cân tại A

=> ∠B = ∠C (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: ∠B = ∠D₁

Hay ΔBFD cân tại F =>BF = DF (3)

Nối AD. Xét ΔAFD và ΔDEA có:

∠ADF =∠EAD(so le trong vì DF // AC)

AD cạnh chung

∠DAF =∠ADE (so le trong vì DE // AB)

Suy ra: ΔAFD= ΔDEA(g.c.g)

Nên AF = DE (hai cạnh tương ứng) (4)

Từ(3) và (4) suy ra: DE + DF = AF + BF = AB = 3cm

Giải Bài 77 trang 148 sách bài tập Toán 7 Tập 1

Cho tam giác đều ABC. Lấy các điểm D, E , F theo thứ tự thuộc các cạnh AB, BC và CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều?

Lời giải:

Ta có: AB = AD +DB (1)

BC = BE + EC (2)

AC = AF + FC (3)

AB = AC = BC ( vì tam giác ABC là tam giác đều) (4)

AD = BE = CF ( giả thiết) (5)

Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF

Xét ΔADF và ΔBED, ta có:

AD = BE (gt)

∠A =∠B =60^o (vì tam giác ABC đều)

AF = BD (chứng minh trên)

suy ra: ΔADF= ΔBED (c.g.c)

⇒ DF=ED (hai cạnh tương ứng) (6)

Xét ΔADF và ΔCFE, ta có:

AD = CF (gt)

∠A =∠C =60^o (vì tam giác ABC đều)

AF = CE (chứng minh trên)

suy ra: ΔADF= ΔCFE (c.g.c)

Nên: DF = FE (hai cạnh tương ứng) (7)

Từ (6) và (7) suy ra: DF = ED = FE

Vậy tam giác DFE đều

Giải Bài 78 Tập 1 trang 148 sách bài tập Toán 7 

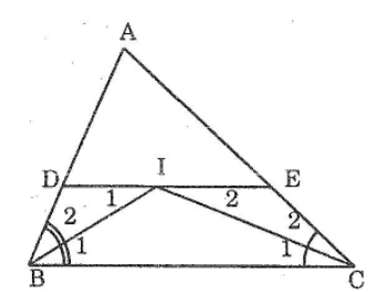
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D,E.

Chứng minh rằng: DE = BD + CE

Lời giải:

Ta có: DI // BC (giả thiết)

Suy ra:∠I₁ =∠B₁(so le trong) (1)

Lại có:∠B₁ =∠B₂ (2)

(vì BI là tia phân giác góc ABC)

Từ (1) và (2) suy ra:∠I₁ =∠B₂

=>∆BDI cân tại D =>BD=DI (3)

Mà IE // BC (gt) => ∠I₂ =∠C₁ (so le trong) (4)

Đồng thời: ∠C₁=∠C₂ (vì CI là phân giác của góc ACB) (5)

Từ (4) và (5) suy ra: ∠I₂=∠C₂. Suy ra ∠CEI cân tại E

Suy ra: CE = EI (6)

Từ (3) và (6) suy ra: BD + CE = DI + EI = DE

Giải Bài 79 trang 148 SBT Toán 7 Tập 1

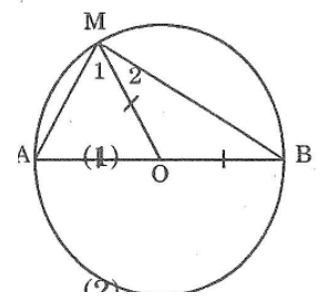
Cho đường tròn tâm O đường kính AB. Gọi M là điểm nằm trên đường tròn, tính số đo góc AMB.

Lời giải:

Nối OM, ta có:

OA = OM (bán kính đường tròn tâm O)

Nên ΔOAM cân tại O

⇒∠A =∠M₁(tính chất tam giác cân)(1)

OM = OB (bán kính đường tròn tâm O)

Suy ra: ΔOBM cân tại O

⇒∠B =∠M₂(tính chất tam giác cân) (2)

Trong ΔAMB ta có:

∠A + ∠AMB + ∠B = 180º (tổng ba góc trong tam giác)

⇒∠A +∠B +∠M₁+∠M₂ =180 (3)

Từ (1), (2) và (3) suy ra: 2(∠M₁ + ∠M₂)=180^o

Vậy: ∠M₁+∠M₂=90^o hay ∠(AMB) =90^o

Giải trang 148 sách bài tập Toán 7 Bài 80 Tập 1

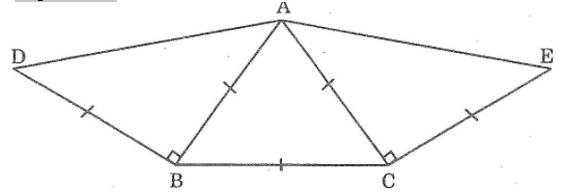
Đặt đề toán theo hình dưới đây. Sau đó vẽ lại hình theo đề toán rồi đo goác DAE

Lời giải:

Đề toán:

Vẽ tam giác ABC đều

Vẽ tam giác ABD vuông cân tại B sao cho D và C nằm trên hai nửa mặt phẳng bờ chứa đường thẳng AB.

Vẽ tam giác ACE vuông cân tại C sao cho E và B nằm trên hai nửa mặt phẳng đối có bờ chứa đường thẳng AC

Đo ∠DAE =150^o

Chứng minh:

Giải Bài 81 trang 148 sách bài tập Toán 7 

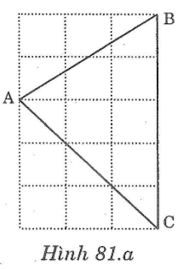
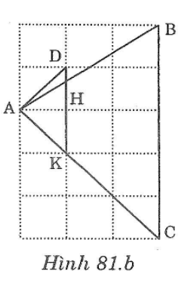
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới ) là tam giác nhọn.

Lời giải:

Nối A với D tạo thành đường chéo ô vuông

Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ngang ô vuông đi qua A. ( như hình vẽ)

Ta có: ΔAHK vuông cân tại H =>∠HAK =45^o

ΔAHD vuông cân tại H=>∠HAD =45^o

=>∠DAK =∠HAK +∠HAD =45^o+45^o=90^o

hay ∠DAC =90^o

=>∠BAC <90^o

Hình vuông có 4 góc, mỗi góc bằng 900. Từ hình vẽ suy ra: ∠ACB <90^o và ∠ABC <90^o

Vậy tam giác ABC là tam giác nhọn

CLICK NGAY vào nút TẢI VỀ dưới đây để tải Giải SBT Toán 7 trang 147, 148 file word, pdf hoàn toàn miễn phí