Giải Toán lớp 9 VNEN Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

Nội dung hướng dẫn giải Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông được chúng tôi biên soạn bám sát bộ sách giáo khoa môn Toán chương trình mới (VNEN). Là tài liệu tham khảo hữu ích giúp các em học tốt môn Toán lớp 9.

A.B. Hoạt động khởi động và hình thành kiến thức - Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

a) Em thực hiện hoạt động sau

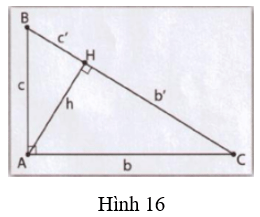
- Dựa vào các tỉ số đồng dạng của các tam giác tìm được, em hoàn thành các đẳng thức sau:

AC² = CH x ….

AB² = BH x ….

b² = ……….

c² = ………..

Trả lời:

- Các tam giác đồng dạng với tam giác ABH là tam giác CBA, tam giác CAH.

- AC² = CH x CB

b² = b'.(b' + c') ;

AB² = BH x BC

c² = c'.(b' + c').

b) Đọc kĩ nội dung sau

Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của các cạnh góc vuông đó trên cạnh huyền.

Cụ thể, trong tam giác vuông ABC, AB = c, BC = a, CA = b, đường cao AH = h, BH = c’, CH = b’ ta có: b² = ab’ ; c² = ac’. (1)

Áp dụng: Cho a = 8cm, b = 6cm. Tính b’, c’.

Ta có: b² = ab’

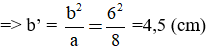
c' = a – b’ = 8 – 4,5 = 3,5 (cm)

c) Áp dụng công thức b² = ab’, c² = ac’ để làm bài tập sau

Bài tập 1. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6, BC = 10

 

Tính độ dài x, y trên hình 17. Điền vào chỗ chấm (…) để hoàn thành lời giải.

Gợi ý. Áp dụng công thức b² = ab’, c² = ac’ cho tam giác vuông ………, đường cao ………… :

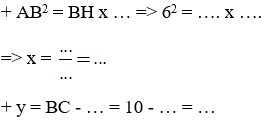
Trả lời:

Áp dụng công thức b² = ab', c² = ac' cho tam giác vuông ABC đường cao AH:

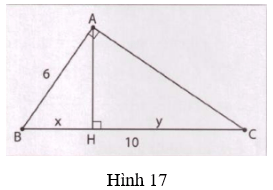
+ AB² = BH x BC ⇒ 62 = x.(x + y)

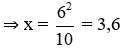
+ y = BC - 3,6 = 10 - 3,6 = 6,4.

2. Một số hệ thức liên quan tới đường cao

a) Em điền vào chỗ chấm (…) để hoàn thành chứng minh sau

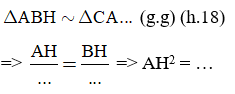
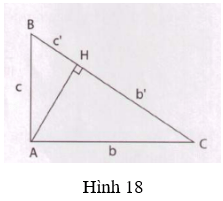
Lời giải:

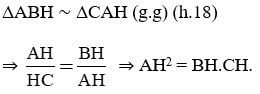
b) Đọc kĩ nội dung sau

Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.

h² = b’.c’ (2)

Bài tập 2. Áp dụng công thức h² = b’.c’, tính x trong hình 19. Điền vào chỗ chấm (…) để hoàn thành lời giải.

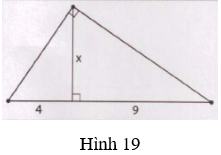
Áp dụng công thức h² = b’.c’, ta có:

x² = ………….. ⇒ x = …………

Trả lời:

Áp dụng công thức h² = b'.c', ta có:

x² = 4.9

⇒ x = 6

c) Đọc kĩ nội dung sau

Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.

bc = ah (3)

Bài tập 3. Cho tam giác vuông với hai cạnh góc vuông lần lượt là 6cm và 8cm (h.20). Tính độ dài đường cao ứng với cạnh huyền của tam giác. Em hãy điền vào chỗ chấm (…) để hoàn thành lời giải.

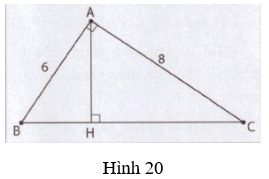
Gợi ý. Theo định lý Py-ta-go

BC² = ……… = ……… = ……….

- Áp dụng công thức bc = ah, ta có

AB x …. = ….. x AH ⇒ AH = ...

Trả lời:

Theo định lý Py-ta-go

BC² = AB² + AC² = 6² + 8² = 100.

- Áp dụng công thức bc = ah, ta có:

AB.AC = BC.AH

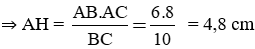
d) Đọc kĩ nội dung sau

Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.

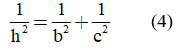
• Em hãy sử dụng công thức 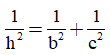 để tính độ dài đường cao trong bài tập 3 và ghi vào vở.

- So sánh kết quả với cách làm ở trên.

Trả lời:

Áp dụng công thức 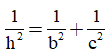 , ta có:

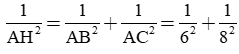
⇒ AH = 4,8 cm.

- Kết quả tính AH ở hai cách làm bằng nhau.

C. Hoạt động luyện tập - Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

Câu 1: (trang 60 SGK VNEN Toán 9 tập 1 chương 1)

Tính x, y trong mỗi hình sau:

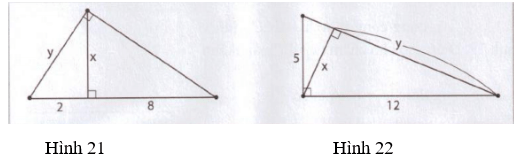
Lời giải:

* Hình 21

Áp dụng công thức b² = b'.a', ta có:

y² = 2.(2 + 8) = 20 ⇒ y = 2

Áp dụng công thức h2 = b'.c', ta có:

x² = 2.8 = 16 ⇒ x = 4.

* Hình 22:

Áp dụng công thức 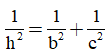 , ta có:

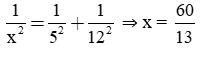
Áp dụng định lý Py-ta-go, ta có:

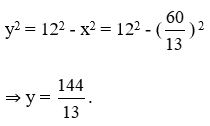
Câu 2: (trang 61 SGK Toán 9 VNEN tập 1 chương 1)

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 3cm và 12cm. Hãy vè hình và tính các cạnh góc vuông của tam giác này.

Bài làm:

Ta được hình vẽ:

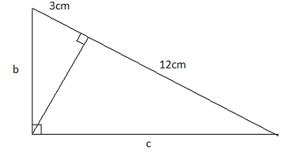
* Áp dụng công thức c² = c'.a, ta có:

c² = 12.(12 + 3) = 180

⇒ c = 6 cm.

* Áp dụng công thức b² = b'.a, ta có:

b² = 3.(12 + 3) = 45

⇒ c = 3 cm

Câu 3: (trang 61 SGK Toán lớp 9 VNEN tập 1 chương 1)

Nam vẽ một tam giác vuông trên giấy kẻ ô li, hai cạnh góc vuông nằm tương ứng trên hai đường kẻ dọc và ngang của quyển vở, lần lượt ứng với 3 ô li và 4 ô li. Tiếp theo Nam kẻ đường cao ứng với cạnh huyền. Tính độ dài đường cao đó.

Lời giải:

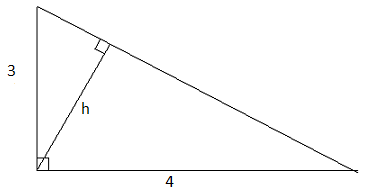
Gọi đường cao của tam giác vuông Nam kẻ được là h

Áp dụng công thức 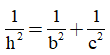 , ta có:

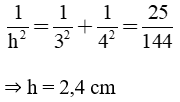
Câu 4: (trang 61 SGK Toán VNEN lớp 9 tập 1 chương 1)

Cho hình chữ nhật ABCD có cạnh BC = 6cm, AB = 8cm. Đường thẳng kẻ từ B vuông góc với AC tại E, cắt cạnh AD tại F

a) Tính độ dài các đoạn thẳng AC, AE, BE.

b) Tính độ dài các cạnh và diện tích tam giác ABF

Lời giải:

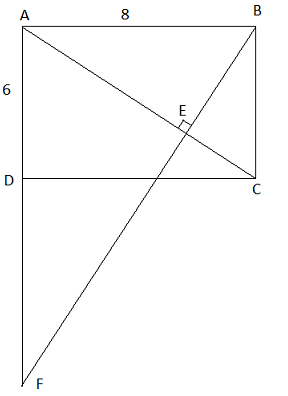
a) * AC² = AB² + BC² = 6² + 8² = 100

⇒ AC = 10 cm

* Áp dụng công thức b² = b.a', ta có:

AB² = AE.AC

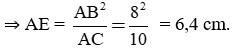
* Áp dụng định lý Py-ta-go, ta có:

BE² = AB² - AE² = 8² - 6,4² = 23,04

⇒ BE = 4,8 cm.

b) Tam giác ABF có cạnh AB = 8 cm

* Áp dụng công thức 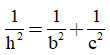 , ta có:

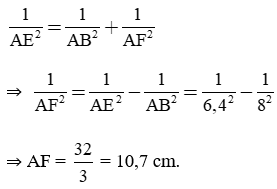
* Áp dụng định lý Py-ta-go, ta có:

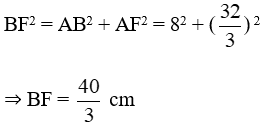
* Diện tích tam giác ABF là

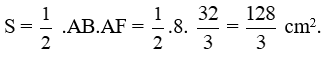
D.E. Hoạt động vận dụng và tìm tòi, mở rộng - Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

1. Kiểm chứng công thức h² = b’c’ bằng cắt ghép hình

Chuẩn bị:

- Hai miếng bìa hình tam giác vuông bằng nhau có đường cao bằng h, hình chiếu của hai cạnh góc vuông xuống cạnh huyền lần lượt là b’, c’; một miếng bìa hình vuông cạnh h và một miếng bìa hình chữ nhật cạnh b’, c’ (h.23a).

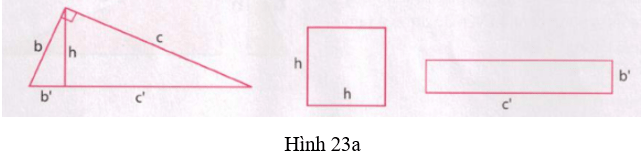
Bước 1: Cắt hai miếng bìa hình tam giác vuông theo đường cao hạ từ đỉnh góc vuông xuống cạnh huyền để được 4 tam giác vuông (h.23b)

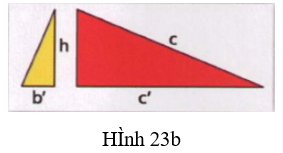
Bước 2: Dùng 2 miếng bìa hình tam giác vuông vừa được cắt ra từ tam giác vuông ban đầu và một miếng bìa hình vuông cạnh h ghép thành tam giác vuông như hình 23c.

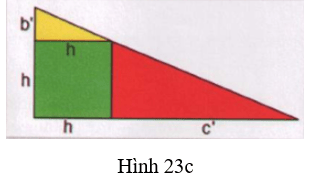
Bước 3: Dùng 2 miếng bài hình tam giác vuông vừa được cắt ra từ tam giác vuông ban đầu và một miếng bìa hình chữ nhật ghép thành tam giác vuông như hình 23d.

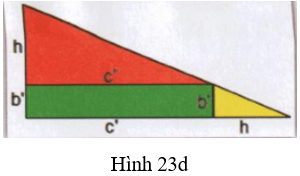
Hãy:

- So sánh hai tam giác vuông tạo thành từ hai lần ghép hình trên (hình 23c, 23d).

- So sánh diện tích hình vuông cạnh h và hình chữ nhật cạnh b’ và c’ ban đầu. Từ đó rút ra nhận xét gì về h2 và b’.c’.

2. Kiểm chứng công thức bc = ah bằng cắt ghép hình

Chuẩn bị: Hai miếng bìa hình tam giác vuông bằng nhau có ba cạnh lần lượt là: a, b, c đường cao d=ứng với cạnh huyền a là h (h.24a).

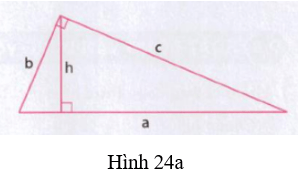
Bước 1: Cắt hai miếng bìa hình tam giác theo đường cao hạ từ đỉnh góc vuông xuống cạn huyền để được 4 tam giác vuông (h.24b).

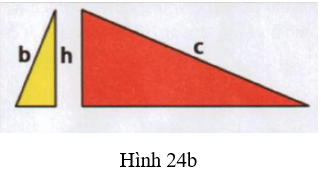
Bước 2: Ghép 4 tam giác vuông này thành một hình chữ nhật như hình 24c.

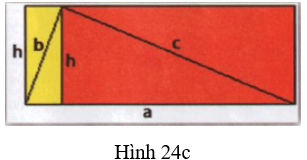
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông VNEN Toán 9 file PDF hoàn toàn miễn phí.