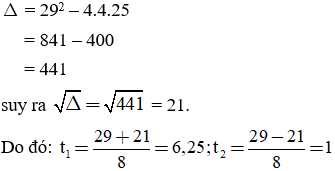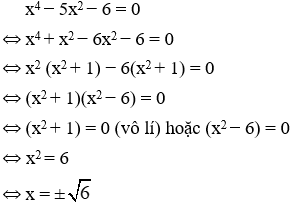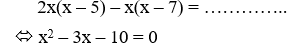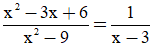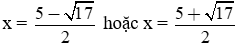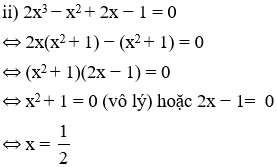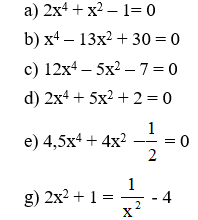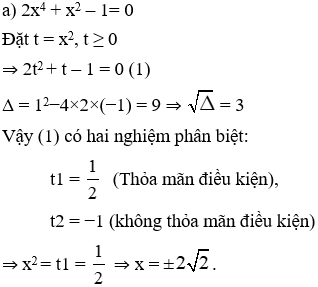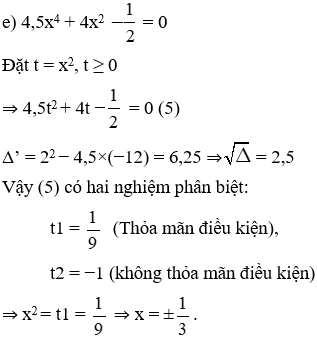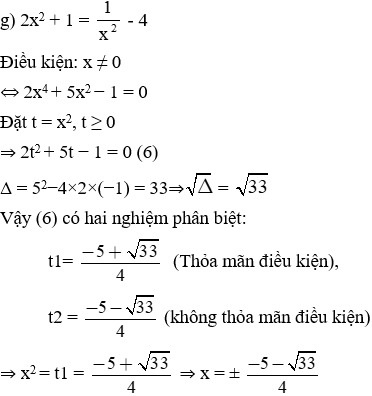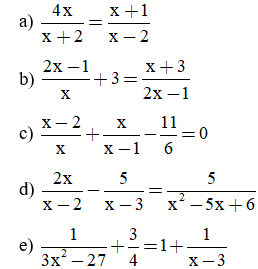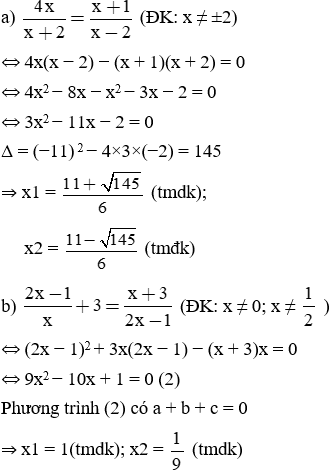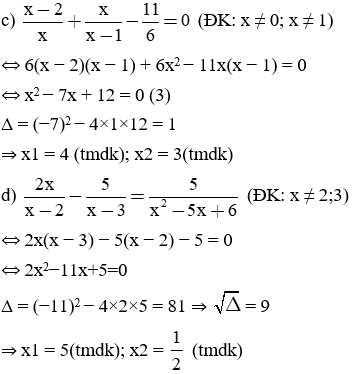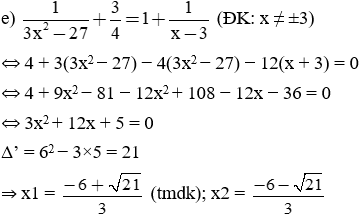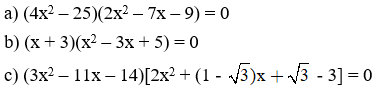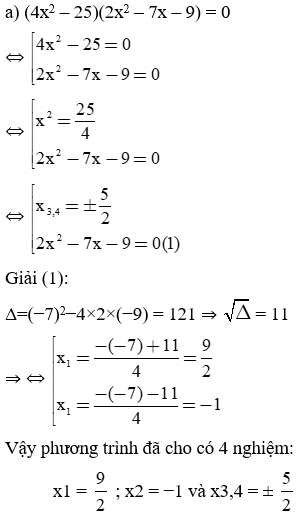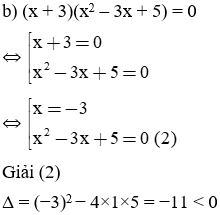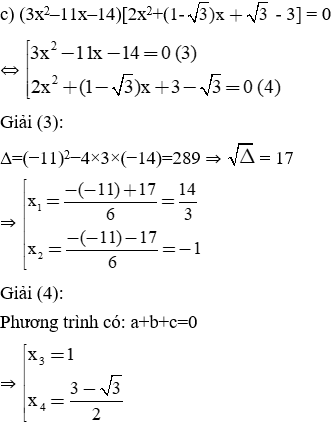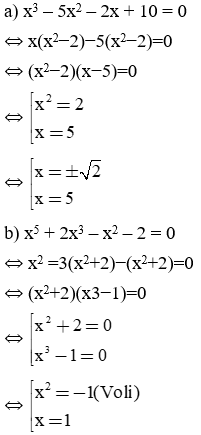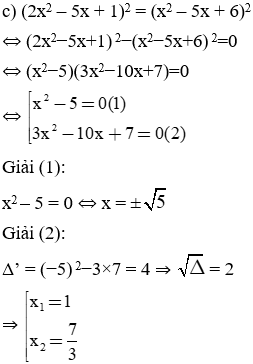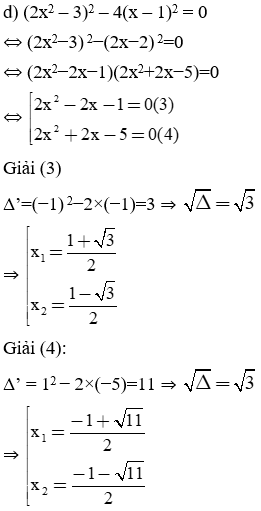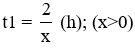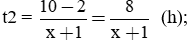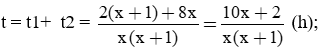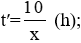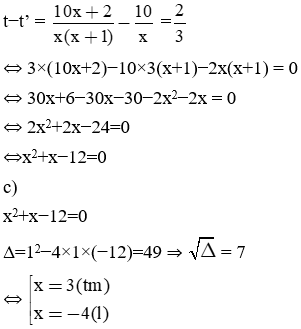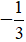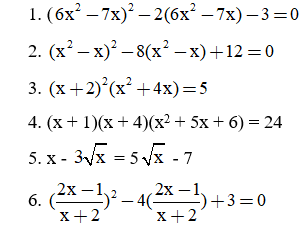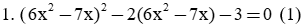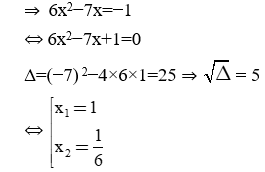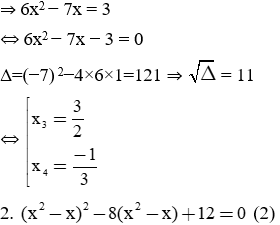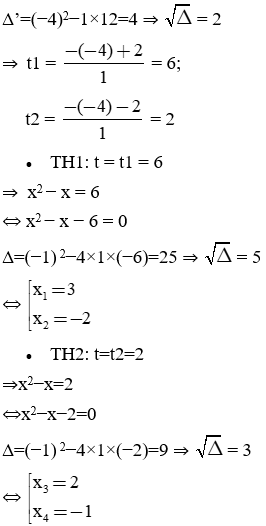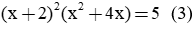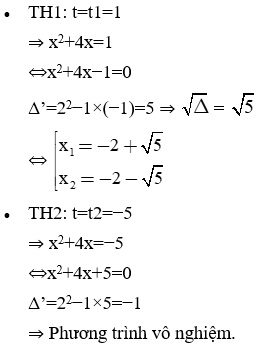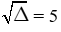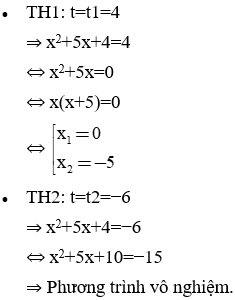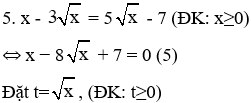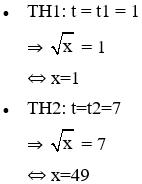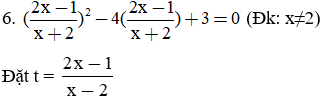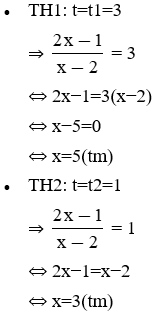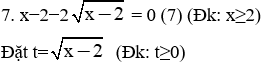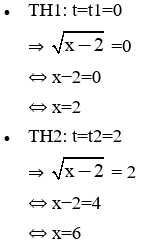Giải Toán lớp 9 VNEN Bài 8: Phương trình quy về phương trình bậc hai

Nội dung hướng dẫn giải Bài 8: Phương trình quy về phương trình bậc hai được chúng tôi biên soạn bám sát bộ sách giáo khoa môn Toán chương trình mới (VNEN). Là tài liệu tham khảo hữu ích giúp các em học tốt môn Toán lớp 9.

A.B. Hoạt động khởi động và hình thành kiến thức - Bài 8: Phương trình quy về phương trình bậc hai

1. a) Thực hiện các hoạt động sau

Xét các phương trình

i) x⁴ – 5x² – 6 = 0

ii) 8x⁴ – x² – 7 = 0

iii) 4x⁴ + 7x² – 2 = 0

- Các phương trình trên có đặc điểm gì chung? Dựa vào đặc điểm chung này, hãy viết dạng tổng quát cho các phương trình đó.

- Giải phương trình x⁴ – 5x² - 6 = 0 bằng các cách có thể.

- Có thể đưa việc giải phương trình x⁴ – 5x² - 6 = 0 về giải một phương trình bậc hai được không? Hãy đề xuất cách giải đó.

- Hãy thảo luận để đưa ra một phương án chung giải các phương trình dạng này.

b) Đọc kĩ nội dung sau

* Phương trình trùng phương là phương trình có dạng:

   ax⁴ + bx² + c = 0 (a ≠ 0) (1)

* Có thể đưa phương trình trùng phương về phương trình bậc hai bằng cách đặt ẩn phụ như sau:

Đặt x² = t ≥ 0, phương trình (1) trở thành phương trình bậc hai

   at² + bt + c = 0

c) Giải các phương trình trùng phương sau (theo mẫu)

i) 8x⁴ – x² – 7 = 0

ii) 4x⁴ + 7x² – 2 = 0

Mẫu: Giải phương trình 4x⁴ – 29x² + 25 = 0

Giải. Đặt x² = t, t ≥ 0, ta có: 4t² – 29t + 25 = 0.

Cả hai giá trị 6,25 và 1 đều thỏa mãn điều kiện t ≥ 0.

* Với t = t₁ = 6,25, ta có x² = 6,25. Suy ra x₁ = -2,5 ; x₂ = 2,5.

* Với t = t₂ = 1, ta có x² = 1. Suy ra x₃ = -1; x₄ = 1.

Vậy phương trình 4x⁴ – 29x² + 25 = 0 có 4 nghiệm:

  x₁ = -2,5 ;  x₂ = 2,5 ;  x₃ = -1;  x₄ = 1.

Trả lời:

a)

• Đặc điểm chung: Đều là các phương trình bậc 4, các ẩn chỉ có số mũ bậc 2 và bậc 4. Dạng tổng quát cho các phương trình là: ax⁴ + bx² + c = 0.

• Giải phương trình x⁴ − 5x² − 6 = 0 bằng cách có thể.

• Có thể đưa việc giải phương trình x⁴ − 5x² – 6 = 0 về giải một phương trình bậc hai được bằng cách đặt x² = t (ĐK: t ≥ 0)

c)

i) 8x⁴ – x² – 7 = 0

Đặt x² = t, t ≥ 0, ta có: 8t² − t − 7 = 0 (*)

Phương trình (*) có: a + b + c = 0 ⇒ Nghiệm của phương trình (*) là t₁ = 1 > 0 (TM) 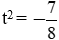 < 0 (loại)

Với t = t₁ = 1 ⇒ x² = 1 ⇒ x = ±1

ii) 4x⁴ + 7x² – 2 = 0

Đặt x² = t, t ≥ 0, ta có: 4t² + 7t – 2 = 0 (**)

2. a) Viết tiếp vào chỗ chấm (…) để giải phương trình 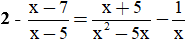 và trả lời các câu hỏi.

Điều kiện: x ≠ ……………

- Khử mẫu và biến đổi, ta được:

- Nghiệm của phương trình x² – 3x – 10 = 0 là x₁ = ……; x₂ = ……

Hỏi x₁ có thỏa mãn điều kiện nói trên không? Tương tự đối với x₂?

Vậy nghiệm của phương trình đã cho là: …………..

b) Đọc kĩ nội dung sau

Giải phương trình chứa ẩn ở mẫu thức

- Bước 1: Tìm điều kiện xác định của phương trình ;

- Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức ;

- Bước 3: Giải phương trình vừa nhận được ;

- Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thỏa mãn điều kiện xác định, các giá trị thỏa mãn điều kiện xác định là nghiệm của phương trình đã cho

c) Giải phương trình: 

Trả lời:

a) Điều kiện: x ≠ 0; x ≠ 5

Khử mẫu và biến đổi ta được: 2x(x − 5) − x(x − 7) = (x + 5) − (x − 5)

⇔ 2x² − 10x – x² + 7x = 10

⇔ x² − 3x – 10 = 0

Nghiệm của phương trình: x² − 3x – 10 = 0 là x₁ = 5; x₂ = −2

Hỏi x₁ = 5 không thỏa mãn điều kiện, x₂ = −2 có thỏa mãn điều kiện

Vậy, nghiệm của phương trình đã cho là: x = −2

c)

Điều kiện: x ≠ ±3

Khử mẫu và biến đổi ta được: x² − 3x + 6 = x + 3 ⇔ x² − 4x + 3 = 0 (2)

Phương trình bậc hai thu được có a + b + c = 0 nên, nghiệm của (2) là:

   x₁ = 1 (Thỏa mãn điều kiện)

   hoặc x₂ = 3 (không thỏa mãn điều kiện)

Vậy, phương trình ban đầu có nghiệm là: x = 1

3. Viết tiếp vào chỗ chấm (…) để giải phương trình tích (x – 5)(x² + 3x + 2) = 0

(x – 5)(x² + 3x + 2) = 0 ⇔ x – 5 = 0 hoặc x² + 3x + 2 = 0

⇔ x = 5 hoặc ……………

Vậy nghiệm của phương trình đã cho là: ………………

b) Đọc kĩ nội dung sau

Để giải phương trình tích dạng A(x).B(x) = 0, ta giải các phương trình A(x) = 0; B(x) = 0. Tất cả các giá trị tìm được của ẩn đều là nghiệm của phương trình A(x).B(x) = 0.

c) Giải phương trình sau bằng cách đưa về phương trình tích

i) 3x³ – 5x² + 2x = 0

ii) 2x³ – x² + 2x – 1 = 0

Trả lời:

a)

(x − 5)(x² + 3x + 2) = 0

⇔ x − 5 = 0 hoặc x² + 3x + 2 = 0

⇔ x = 5 hoặc (x + 1)(x + 2) = 0

⇔ x = 5 hoặc x = −1 hoặc x = −2

c)

i) 3x³ − 5x² + 2x = 0

⇔ x(x² − 5x + 2) = 0

⇔ x = 0 hoặc x² − 5x + 2 = 0 (*)

Giải (*): Δ = (−5)² − 4×1×2 = 17 > 0

Vậy (*) có hai nghiệm phân biệt: 

C. Hoạt động luyện tập - Bài 8: Phương trình quy về phương trình bậc hai

Câu 1: (trang 56 SGK VNEN Toán lớp 9 tập 2 chương 4)

Giải các phương trình sau:

Bài làm:

Câu 2: (trang 57 SGK Toán 9 VNEN tập 2 chương 4)

Giải các phương trình sau:

Bài làm:

Câu 3: (trang 57 SGK Toán lớp 9 VNEN tập 2 chương 4)

Giải các phương trình sau:

Bài làm:

Vậy (2) vô nghiệm.

Vậy, phương trình đã cho có nghiệm duy nhất: x = −3

Câu 4: (trang 57 SGK Toán VNEN lớp 9 tập 2 chương 4)

Giải các phương trình sau bằng cách đưa về phương trình tích:

 a) x³ – 5x² – 2x + 10 = 0

 b) x⁵ + 2x³ – x² – 2 = 0

 c) (2x² – 5x + 1)² = (x² – 5x + 6)²

 d) (2x² – 3)² – 4(x – 1)² = 0

Bài làm:

D. Hoạt động vận dụng - Bài 8: Phương trình quy về phương trình bậc hai

Nam và Bình được đại diện cho trường tham gia cuộc thi chạy ma-ra-tông hạng 10km. Học xuất phát cùng nhau và với cùng vận tốc là x km/h. Sau khi chạy được 2km, Nam tăng vận tốc của mình thêm 1km/h và chạy quãng đường còn lại với vận tốc không đổi là (x + 1) km/h. Bình vẫn duy trì vận tốc của mình trong cả quãng đường đua. Kết quả là Nam đã về đích sớm hơn Bình 40 phút.

a) Viết biểu thức biểu thị thời gian mà Nam hoàn thành quãng đường đua theo biến x.

b) Kết quả cuộc đua cho thấy Nam đã về đích sớm hơn Bình 40 phút. Lập phương trình ẩn x thể hiện giả thiết này và chỉ ra rằng nó có thể được thu gọn thành phương trình bậc hai x² + x – 12 = 0.

c) Giải phương trình x² + x – 12 = 0 để tìm vận tốc xuất phát của Nam và Bình.

Bài làm:

a) Thời gian Nam chạy với vận tốc x (km/h) là:

  

Thời gian Nam chạy với vận tốc (x + 1) km/h là:

  

Tổng thời gian Nam chạy hết đường đua là:

  

b) Thời gian Bình chạy hết quãng đường đua là: 

Đổi: 40 phút = 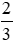 (h)

Nam về đích sớm hơn Bình 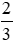 giờ nên:

Vậy, vận tốc khi xuất phát của Nam và Bình là 3 km/h

E. Hoạt động tìm tòi mở rộng - Bài 8: Phương trình quy về phương trình bậc hai

Với nhiều phương trình ta có thể dùng phương pháp đặt ẩn phụ để đưa về một phương trình bậc hai và giải.

Ví dụ. Giải phương trình 3(x² + 5x)² – 2(x² + 5x) – 1 = 0

Hướng dẫn. Đặt t = x² + 5x, ta có phương trình 3t² – 2t – 1 = 0

Giải phương trình 3t² – 2t – 1 = 0 ta được t₁ = 1 và t₂ = 

Thay mỗi giá trị của t vừa tìm được vào đẳng thức t = x² + 5x, ta được một phương trình của ẩn x, Giải mỗi phương tình này sẽ tìm được giá trị của x.

Giải mỗi phương trình sau bằng cách đặt ẩn phụ:

Bài làm:

Đặt t = 6x² − 7x

⇒ Phương trình (1) trở thành: t² − 2t – 3 = 0 (1')

Phương trình (1') có a−b+c=0 nên phương trình (1') có hai nghiệm là: t₁=−1; t₂=3

• TH1: Với t = t₁ = −1

• TH2: Với t = t₂ = 3

Đặt t = x² − x

⇒ Phương trình (2) trở thành: t² − 8t + 12 = 0 (2')

3. 

⇔(x² + 4x + 4)(x² + 4x) = 5

Đặt t = x² + 4x

⇒ Phương trình (3) trở thành: (t + 4)t = 5 ⇔ t² + 4t − 5 = 0 (3')

Phương trình (3') có: a + b + c = 0 nên nghiệm của (3') là:

⇒ t₁ = 1; t₂ = −52

4. (x + 1)(x + 4)(x² + 5x + 6) = 24 (4)

⇔(x² + 5x + 4)(x² + 5x + 6) = 24

Đặt t = x² + 5x + 4

⇒ Phương trình (4) trở thành: t(t + 2) = 24 ⇔ t² + 2t − 24 = 0 (4')

Δ’= 1² − 1×(−24) = 25 ⇒ 

⇒ t₁ = 4; t₂ = −6

⇒ Phương trình (5) trở thành: t² − 8t + 7 = 0 (5')

Phương trình (5') có a + b + c = 0 nên nghiệm của (5') là:

⇒ t₁ = 1 (tm); t₂ = 7 (tm)

⇒ Phương trình (6) trở thành: t² − 4t + 3 = 0 (6')

Phương trình (6') có a + b + c = 0 nên nghiệm của (6') là:

⇒ t₁ = 3; t₂ = 1

⇒ Phương trình (7) trở thành: t² − 2t = 0 (7')

⇔ t(t − 2) = 0

⇔ t₁ = 0 (tm); t₂ = 2 (tm)

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Bài 8: Phương trình quy về phương trình bậc hai VNEN Toán 9 file PDF hoàn toàn miễn phí.