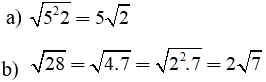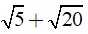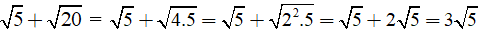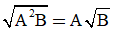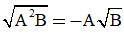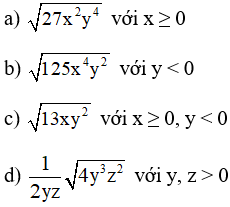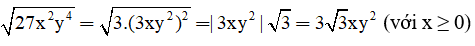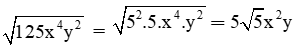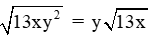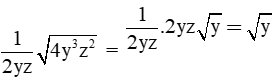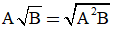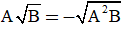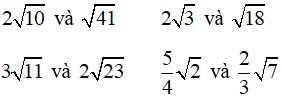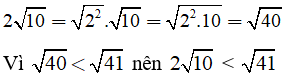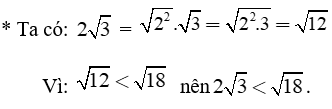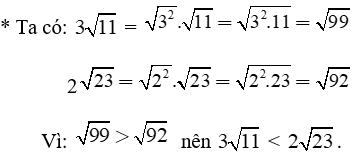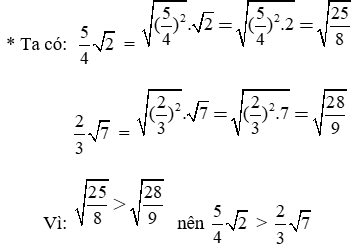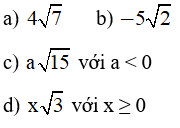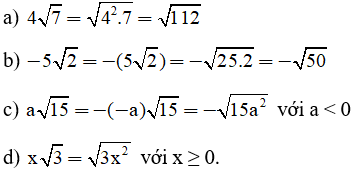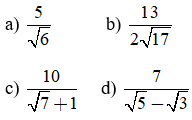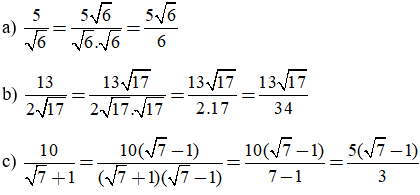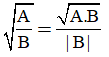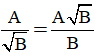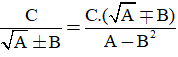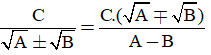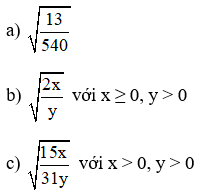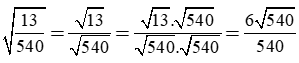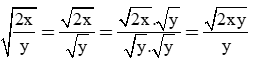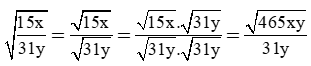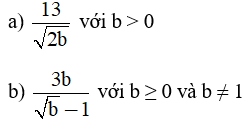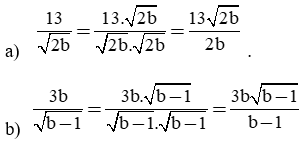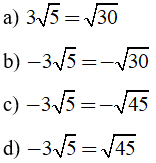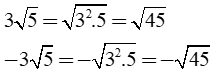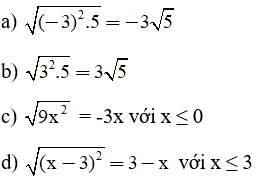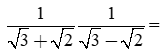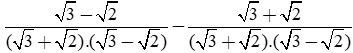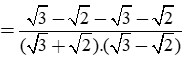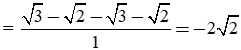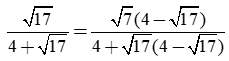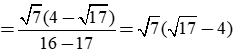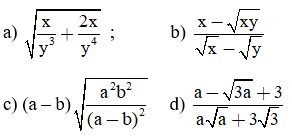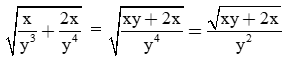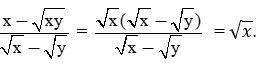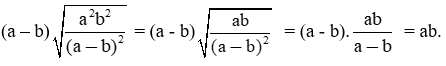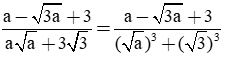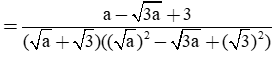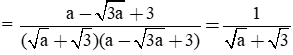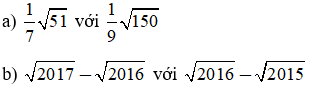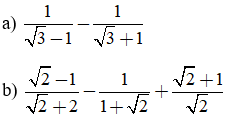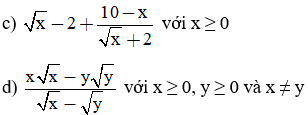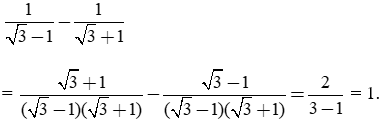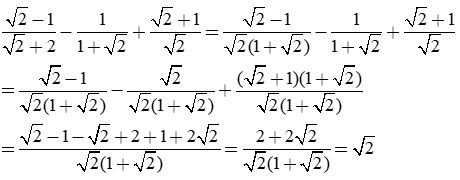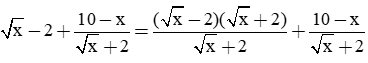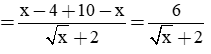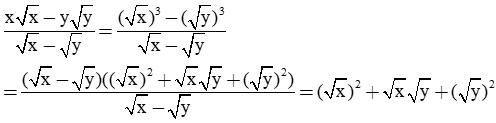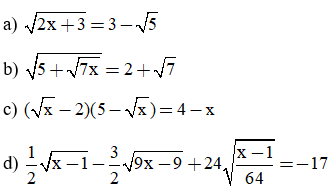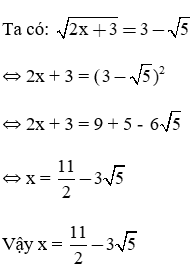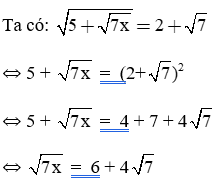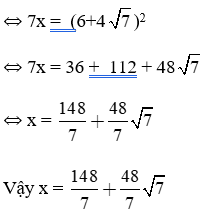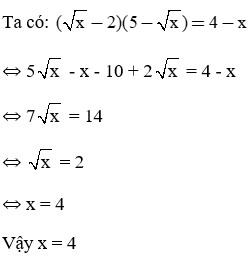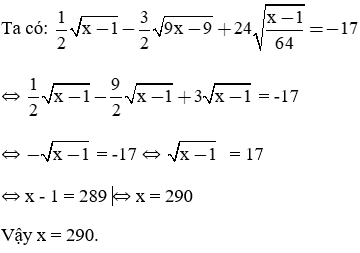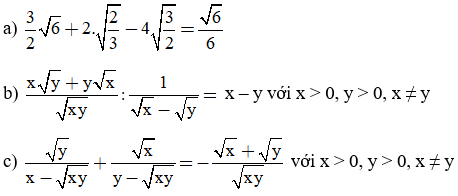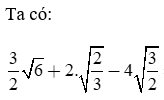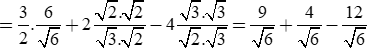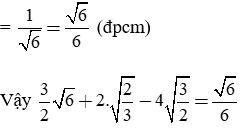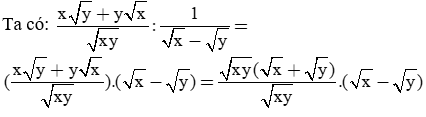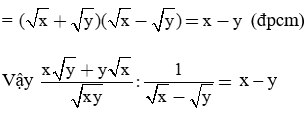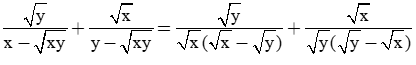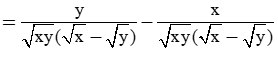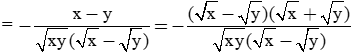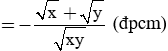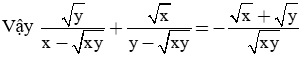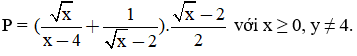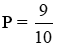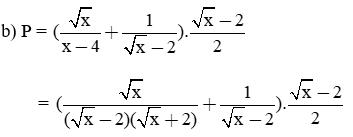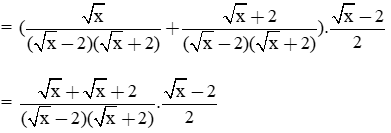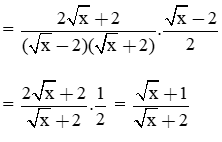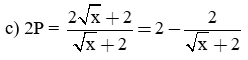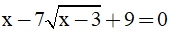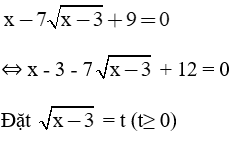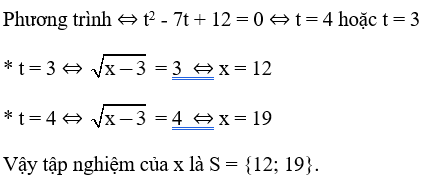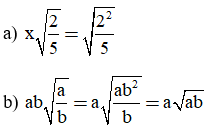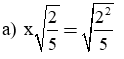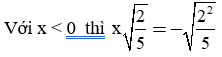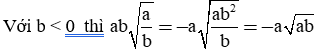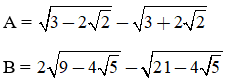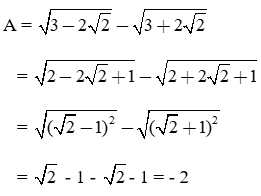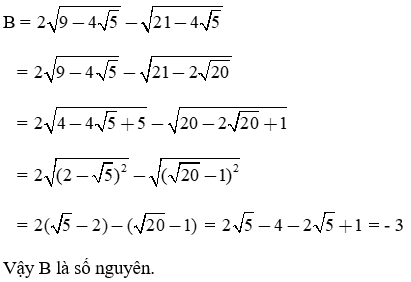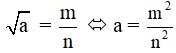Giải Toán lớp 9 VNEN Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Nội dung hướng dẫn giải Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai được chúng tôi biên soạn bám sát bộ sách giáo khoa môn Toán chương trình mới (VNEN). Là tài liệu tham khảo hữu ích giúp các em học tốt môn Toán lớp 9.

A.B. Hoạt động khởi động và hình thành kiến thức - Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

1. a) Đọc hiểu nội dung sau:

Phép biến đổi 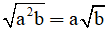 (với a ≥ 0, b ≥ 0) được gọi là đưa thừa số ra ngoài dấu căn.

Ví dụ 1:

Ví dụ 2:

Rút gọn biểu thức 

Giải:

Các biểu thức 2√5 và √5 được gọi là đồng dạng với nhau.

b) Đọc kỹ nội dung sau:

Với hai biểu thức A, B mà B ≥ 0, ta có 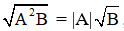 , tức là:

Nếu A ≥ 0 và B ≥ 0 thì 

Nếu A < 0 và B ≥ 0 thì 

Ví dụ: Đưa thừa số ra ngoài dấu căn:

Mẫu:

Trả lời:

b) Ta có:

c) Ta có:

d) Ta có:

2. a) Đọc kĩ nội dung sau:

Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là đưa phép thừa số vào trong dấu căn.

Với A ≥ 0 và B ≥ 0 ta có 

Với A < 0 và B ≥ 0 ta có 

b) So sánh:

Mẫu:

Trả lời:

c) Đưa thừa số vào trong dấu căn:

Hướng dẫn:

3. a) Đọc kĩ nội dung sau:

Khi biến đổi biểu thức chứa căn thức bậc hai, người ta có thể sử dụng phép khử mẫu của biểu thức lấy căn.

b) Trục căn thức ở mẫu:

Hướng dẫn:

Trong ví dụ trên ở câu c) để trục căn thức ở mẫu, ta nhân cả tử và mẫu với biểu thức √7 - 1. Ta gọi biểu thức √7 + 1 và biểu thức √7 - 1 là hai biểu thức liên hợp với nhau. Tương tự, ở câu d) ta nhân cả tử và mẫu với biểu thức liên hợp của √5 - √3 là √5 + √3

4. a) Đọc kĩ nội dung sau:

- Với các biểu thức A, B mà A.B ≥ 0 và B ≠ 0 ta có:

- Với các biểu thức A, B mà B > 0 ta có:

- Với các biểu thức A, B, C mà A ≥ 0 và A² ≠ B², ta có:

- Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0 và A ≠ B ta có:

b) Khử mẫu của biểu thức lấy căn:

Trả lời:

a) Ta có:

b) Ta có:

c) Ta có:

c) Trục căn thức ở mẫu:

Trả lời:

C. Hoạt động luyện tập - Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Câu 1: (trang 22 SGK VNEN Toán 9 tập 1 chương 1)

Khẳng định nào sau đây là đúng?

Lời giải:

Ta có:

Suy ra khẳng định C đúng

Câu 2: (trang 23 SGK Toán 9 VNEN tập 1 chương 1)

Khẳng định nào sau đây là sai?

Lời giải:

Ta có:

 suy ra a sai. b đúng

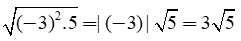
Ta có: với 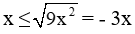 vì -3x > 0 và (−3x)² = 9x² suy ra c đúng

Ta có: x ≤ 3

 và (3 − x)² = (x − 3)² suy ra d đúng

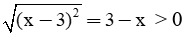
Vậy a và b sai.

Câu 3: (trang 23 SGK Toán lớp 9 tập 1 chương 1)

Khoanh vào chữ đặt trước câu trả lời đúng:

Giá trị của biểu thức 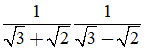 bằng:

A. 0     B. 4

C. 2√2     D. -2√2

Lời giải:

Ta có:

Suy ra đáp án là D.

Câu 4: (trang 23 SGK Toán VNEN lớp 9 tập 1 chương 1)

Khoanh vào chữ đặt trước câu trả lời đúng:

Trục căn thức ở mẫu của 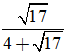 ta được:

A. 4     B. 1/4

C. √17 (4 - √17)    D. √17 (√17 - 4)

Lời giải:

Ta có:

Suy ra đáp án là D.

Câu 5: (trang 23 SGK Toán 9 VNEN tập 1 chương 1)

Rút gọn các biểu thức (giả sử các biểu thức đều có nghĩa):

Lời giải:

a) Ta có:

b) Ta có:

c) Ta có:

d) Ta có:

Câu 6: (trang 23 SGK VNEN Toán lớp 9 tập 1 chương 1)

So sánh (không dùng bảng số hay máy tính cầm tay):

Câu 7: (trang 23 SGK Toán 9 VNEN tập 1 chương 1)

Thực hiện phép tính:

Lời giải:

Giải câu a)

Giải câu b)

Giải câu c)

Giải câu d)

Câu 8: (trang 23 SGK Toán lớp 9 VNEN tập 1 chương 1)

Tìm x, biết:

Lời giải:

Giải câu a)

Giải câu b)

Giải câu c)

Giải câu d)

Câu 9: (trang 24 SGK VNEN Toán lớp 9 tập 1 chương 1)

Chứng minh đẳng thức:

Lời giải:

Giải câu a)

Giải câu b)

Giải câu c)

Câu 10: (trang 24 SGK Toán 9 VNEN tập 1 chương 1)

Cho biểu thức:

a) Tìm giá trị của P khi x = 64.

b) Rút gọn biểu thức P

c) Tìm các giá trị của x để biểu thức 2P nhận giá trị nguyên.

Bài làm:

a) Với x = 64 thì

Để 2P nguyên thì 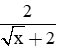 phải nguyên hay √x + 2 là ước của 2

Vì √x ≥ 0 nên √x + 2 ≥ 2

Suy ra √x + 2 = 2 ⇔ x = 0

Vậy x = 0.

D. Hoạt động vận dụng - Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Câu 1: (trang 24 SGK VNEN Toán lớp 9 tập 1 chương 1)

Giải phương trình: 

Bài làm:

Câu 2: (trang 24 SGK Toán VNEN lớp 9 tập 1 chương 1)

Chỉ ra chố sai trong các biến đổi sau:

Bài làm:

Biến đổi trên sai trong trường hợp x < 0

b) Biến đổi trên sai trong trường hợp b < 0

Câu 3: (trang 24 SGK Toán 9 VNEN tập 1 chương 1)

Chứng minh giá trị của các biểu thức sau là nguyên:

Bài làm:

E. Hoạt động tìm tòi, hoạt động - Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Em có biết?

1: Biết diện tích Trái Đất khoảng 510 triệu km², em hãy tính ước lượng bán kính Trái Đất và độ dài đường tròn xích đạo.

Lời giải:

Gọi bán kính của Trái Đất là R (km) (R > 0).

Diện tích Trái Đất là 510 triệu km² tức là πR² = 510 ⇔ R = 12,7 km

Độ dài đường tròn xích đạo chính là chu vi của Trái Đất C = 2πR = 80.1 km

Vậy bán kính Trái Đất là 12,7km, độ dài đường tròn xích đạo là 80,1km.

2. Cho một số tự nhiên a. Nếu a là số chính phương thì √a là một số tự nhiên. Nếu a không là số chính phương thì √a là số vô tỉ.

Chứng minh:

Gọi a là số không chính phương mà √a là một số hữu tỉ.

Do √a là số hữu tỉ nên 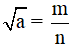 (m,n ∈ N, n > 1 và (m, n) = 1).

Ta có: 

⇔ m² = an². Gọi p là một ước nguyên tố của n thì n 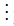 p ⇒ m²  p ⇒ m  p ⇒ và (m,n) = p trái với (m,n) = 1. Vậy √a là số vô tỉ.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai VNEN Toán 9 file PDF hoàn toàn miễn phí.