Giải Toán lớp 9 VNEN Bài 3: Luyện tập về phép nhân và phép khai phương

Nội dung hướng dẫn giải Bài 3: Luyện tập về phép nhân và phép khai phương được chúng tôi biên soạn bám sát bộ sách giáo khoa môn Toán chương trình mới (VNEN). Là tài liệu tham khảo hữu ích giúp các em học tốt môn Toán lớp 9.

C. Hoạt động luyện tập - Bài 3: Luyện tập về phép nhân và phép khai phương

Câu 1: (trang 10 SGK Toán 9 VNEN tập 1 chương 1)

Áp dụng quy tắc khai phương một tích, hãy tính:

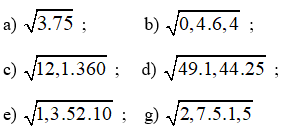
Bài làm

Giải câu a)

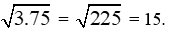
Giải câu b)

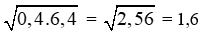
Giải câu c)

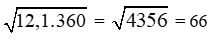
Giải câu d)

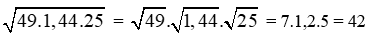
Giải câu e)

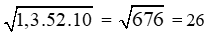
Giải câu g)

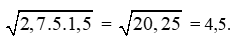
Câu 2: (trang 10 SGK VNEN Toán 9 tập 1 chương 1)

Thực hiện các phép tính sau:

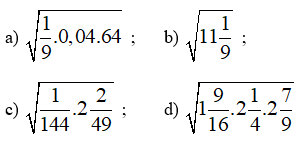
Bài làm

Giải câu a)

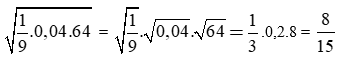
Giải câu b)

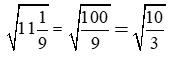
Giải câu c)

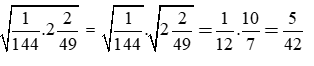
Giải câu d)

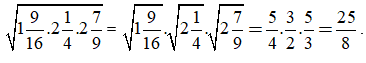
Câu 3: (trang 10 SGK Toán VNEN lớp 9 tập 1 chương 1)

Áp dụng quy tắc nhân hai căn bậc hai, hãy tính:

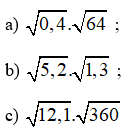
Lời giải:

Giải câu a)

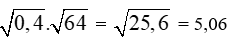
Giải câu b)

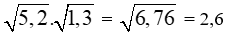
Giải câu c)

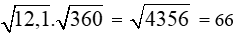
Câu 4: (trang 10 SGK Toán lớp 9 VNEN tập 1 chương 1)

Khẳng định nào sau đây là đúng?

A. Số nghịch đảo của √3 là 1/3

B. Số nghịch đảo của 2 là 1/√2

C. (√2 + √3) và (√2 - √3) không là hai số nghịch đảo của nhau

D. (√5 - √7) và (√5 + √7) là hai số nghịch đảo của nhau

Lời giải:

A. Sai. Vì số nghịch đảo của √3 là 1/√3 chứ không phải là .

B. Sai. Vì số nghịch đảo của 2 là 1/2 chứ không phải là 1/√2.

C. Đúng. Vì (√2 + √3).(√2 - √3) = 2 - 3 = - 1 suy ra (√2 + √3) và (√2 - √3) không là hai số nghịch đảo của nhau.

D. Sai. Vì (√5 - √7).(√5 + √7) = 5 - 7 = - 2 suy ra (√5 - √7) và (√5 + √7) không là hai số nghịch đảo của nhau.

Câu 5: (trang 11 SGK Toán 9 VNEN tập 1 chương 1)

Rút gọn các biểu thức sau:

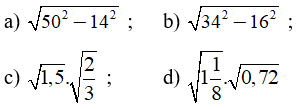
Bài làm

Giải câu a)

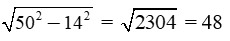
Giải câu b)

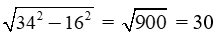
Giải câu c)

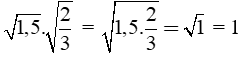
Câu 6: (trang 11 SGK VNEN Toán 9 tập 1 chương 1)

Tính:

a) √(a²) với a = 6,5; -0,1;

b) √(a⁴) với a = 3; -0,1;

c) √(a⁶) với a = -2; 0,1

Lời giải:

Giải câu a)

Với a = 6,5 > 0 thì √(a²) = a = 6,5

Với a = - 0,1 < 0 thì √(a²) = - a = 0,1

Giải câu b)

Với a = 3 > 0 thì √(a⁴)= a² = 3² = 9

Với a = - 0,1 < 0 thì √(a⁴)= (−a)² = (0,1)² = 0,01

Giải câu c)

Với a = -2 < 0 thì √(a⁶) = (−a)³ = (2)³ = 8

Với a = 0,1 < 0 thì √(a⁶) = a³ = 0,13 = 0,001

D. Hoạt động vận dụng - Bài 3: Luyện tập về phép nhân và phép khai phương

Câu 1: (trang 11 SGK Toán lớp 9 VNEN tập 1 chương 1)

Tính:

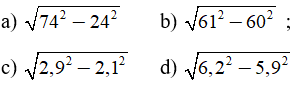
Bài làm

Giải câu a)

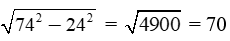
Giải câu b)

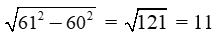
Giải câu c)

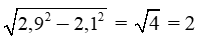
Giải câu d)

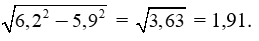
Câu 2: (trang 11 SGK Toán 9 VNEN tập 1 chương 1)

Chứng minh:

a) (2 - √3)(2 + √3) = 1

b) (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau

Bài làm

a) Ta có:

(2 - √3)(2 + √3) = 4 - 3 = 1 (đpcm)

b) Ta có:

(√2006 - √2005).(√2006 + √2005) = 2006 - 2005 = 1

Suy ra (√2006 - √2005)

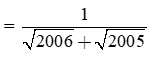
Hay (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau.

Câu 3: (trang 11 SGK Toán lớp 9 VNEN tập 1 chương 1)

So sánh (không dùng bằng số hay máy tính bỏ túi):

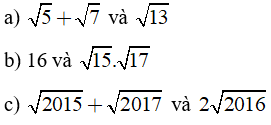
Bài làm

Giải câu a)

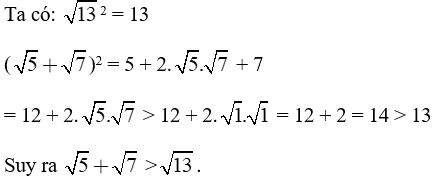
Giải câu b)

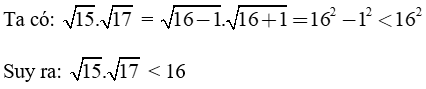
Giải câu c)

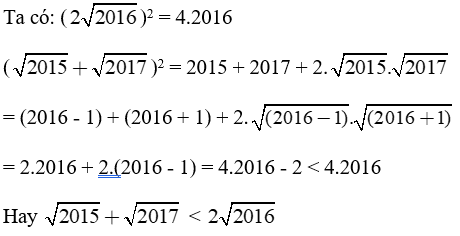
Câu 4: (trang 11 SGK VNEN Toán 9 tập 1 chương 1)

Chứng minh rằng √2 không thể là trung bình cộng của số √3 và √5

Giả sử √2 không thể là trung bình cộng của số √3 và √5tức là:

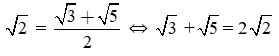
Ta có: (2√2)² = 8

(√3 + √5)² = 3 + 5 + 2.√3.√5 = 8 + 2.√3.√5 > 8

Suy ra √3 + √5 - 2√2 ≠ 0 hay √2 không phải là trung bình cộng của số √3 và √5.

E. Hoạt động tìm tòi, mở rộng - Bài 3: Luyện tập về phép nhân và phép khai phương

Em có biết?

Trong môn Vật lý, ta có định luật Jun Len xơ để tính nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua: Q = I2Rt, trong đó:

Q: Là nhiệt lượng tỏa ra trên dây dẫn (J)

I: Là cường độ dòng điện chạy trong dây dẫn (A)

R: Là điện trở của dây dẫn (Ω)

t: Là thời gian dòng điện chạy qua dây dẫn (giây-s)

Áp dụng công thức trên để giải bài toán sau:

Một bếp điện khi hoạt động bình thường cs điện trở R = 80 ω. Tính cường đọ dòng điện qua bếp, biết nhiệt lượng mà bếp tỏa ra trong 1s là 500J.

Lời giải:

Theo công thức ta có nhiệt lượng tỏa ra là:

Q = I²Rt

⇔ 500 = I².80.1

⇔ I² = 6,25

⇔ I = √6,25 = 2,5 (A)

Vậy cường độ dòng điện là I = 2,5 A.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Bài 3: Luyện tập về phép nhân và phép khai phương VNEN Toán 9 file PDF hoàn toàn miễn phí.