Giải toán lớp 11 trang 28, 29 SGK tập 1: Phương trình lượng giác cơ bản

Giải toán lớp 11 trang 28, 29 sách giáo khoa: Phương trình lượng giác cơ bản gồm hướng dẫn giải chi tiết và đáp án 7 bài tapajj phần giải tích 11 phương trình lượng giác cơ bản được trình bày chi tiết và chính xác nhất dưới đây. Mời các bạn tham khảo.

Bài 1 trang 28 SGK giải tích lớp 11

Giải các phương trình sau:

Hướng dẫn giải bài 1:

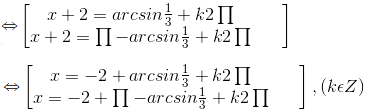
b) sin3x = 1 ⇔ 3x = π/2 + k2π

⇔ x = π/6 + k(2π/3), (k ∈ Z).

(k ∈ Z).

d) Vì -√3/2 = sin(-600) nên phương trình đã cho tương đương với sin (2x + 200) = sin(-600)
⇔

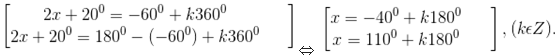
Bài 2 trang 28 sách giáo khoa giải tích lớp 11

Với những giá trị nào của x thì giá trị của các hàm số y = sin3x và y = sinx bằng nhau?

Hướng dẫn giải bài 2:

x thỏa mãn yêu cầu bài ra khi và chỉ khi

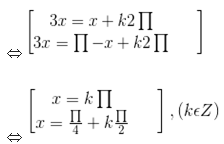
Bài 3 trang 28 giải tích lớp 11 SGK

Giải các phương trình sau:

a) cos(x – 1) = 2/3

b) cos3x = cos120

c) cos(3x/2 – π/4) = -1/2

d) cos22x = 1/4

Hướng dẫn giải bài 3:

a) cos(x - 1) = 2/3 ⇔ x - 1 = ±arccos2/3 + k2π

⇔ x = 1 ± arccos2/3 + k2π, (k ∈Z)

b) cos3x = cos120 ⇔ 3x = ±120 + k3600 ⇔ x = ±40 + k1200, (k ∈ Z).

c) Vì -1/2 = cos2π/3 nên cos(3x/2 - π/4) = -1/2 ⇔ cos(3x/2 - π/4) = cos2/3 ⇔ 3x/2 - π/4 = ±2π/3 + k2π ⇔ x = 2/3(π/4 + 2π/3) + 4kπ/3

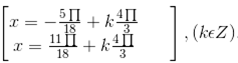
d) Sử dụng công thức hạ bậc 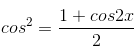 (suy ra trực tiếp từ công thức nhan đôi) ta có

cos22x = 1/4 ⇔ 1 + cos4x/2 = 1/4 ⇔ cos4x = -1/2

⇔ 4x = ±2π/3 + 2kπ ⇔ x = ±π/6 + kπ/2, (k ∈ Z)

Bài 4 giải tích lớp 11 trang 29 SGK

Giải phương trình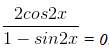 

Hướng dẫn giải bài 4

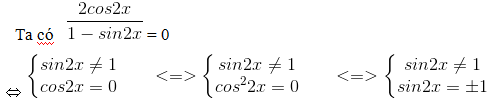
⇔ sin2x = -1 ⇔ 2x = -π/2 + k2π ⇔ x = -π/4 + kπ, (k ∈ Z).

Bài 5 SGK trang 29 giải tích lớp 11

Giải các phương trình sau:

a) tan(x – 150) = (√3)/3 b) cot(3x – 1) = -√3

c) cos2x . tanx = 0 d) sin3x . cotx = 0

Đáp án và hướng dẫn giải bài 5:

a) Vì 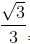= tan300 nên tan(x – 150) =  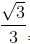⇔ tan(x – 150) = tan300 ⇔ x – 150 = 300 + k1800 ⇔ x = 450 + k1800, (k ∈ Z).

b) Vì -√3 = cot(-π/6) nên cot(3x – 1) = -√3 ⇔ cot(3x – 1) = cot(-π/6)

⇔ 3x – 1 = -π/6 + kπ ⇔ x = -π/18 + 1/3 + k(π/3), (k ∈ Z)

c) Đặt t = tan x thì cos2x = 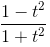 , phương trình đã cho trở thành
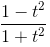. t = 0 ⇔ t ∈ {0; 1; -1} .

Vì vậy phương trình đã cho tương đương với

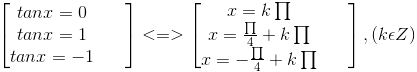
d) sin3x . cotx = 0

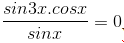⇔ Với điều kiện sinx # 0, phương trình tương đương với

sin3x . cosx = 0 ⇔ sin3x = 0; cos3x = 0

Với cosx = 0 ⇔ x = π/2 + kπ, k ∈ Z thì sin2x = 1 – cos2x = 1 – 0 = 1 => sinx # 0, điều kiện được thỏa mãn.

Với sin3x = 0 ⇔ 3x = kπ ⇔ x = k(π/3), (k ∈ Z). Ta còn phải tìm các k nguyên để x = k(π/3) vi phạm điều kiện (để loại bỏ), tức là phải tìm k nguyên sao cho sink(π/3) = 0, giải phương trình này (với ẩn k nguyên), ta có sink(π/3) = 0 ⇔ k(π/3)= lπ, (l ∈ Z) ⇔ k = 3l ⇔ k : 3.

Do đó phương trình đã cho có nghiệm là x = π/2 + kπ, (k ∈Z) và x = k(π/3) (với k nguyên không chia hết cho 3).

Nhận xét: Các em hãy suy nghĩ và giải thích tại sao trong các phần a, b, c không phải đặt điều kiện có nghĩa và cũng không phải tìm nghiệm ngoại lai.

Bài 6 trang 29 SGK giải tích lớp 11

Với những giá trị nào của x thì gia trị của các hàm số y = tan(π/4 - x) và y = tan2x bằng nhau?

Đáp án và hướng dẫn giải bài 6:

Các giá trị cần tìm của x là các nghiệm của phương trình tan 2x = tan(π/4 – x), giải phương trình này các em có thể xem trong Ví dụ 3b.

Đáp số: π/2 ( k ∈ Z, k – 2 không chia hết cho 3).

Bài 7 SGK giải tích lớp 11 trang 29

Giải các phương trình sau:

a) sin3x – cos5x = 0 b) tan3x . tanx = 1.

Đáp án và hướng dẫn giải bài 7:

a) sin3x – cos5x = 0 ⇔ cos5x = sin3x ⇔ cos5x = cos(π/2 – 3x) ⇔

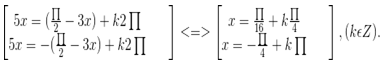
b) tan3x . tanx = 1 ⇔ 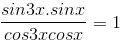 Điều kiện: cos3x . cosx # 0.

Với điều kiện này phương trình tương đương với cos3x . cosx = sin3x . sinx ⇔ cos3x . cosx – sin3x . sinx = 0 ⇔ cos4x = 0.
Do đó

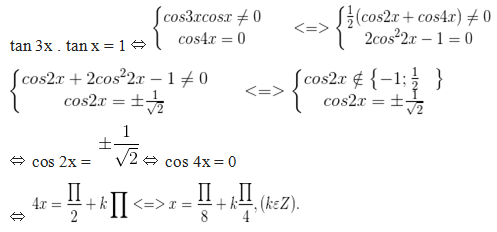
CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải bài Toán lớp 11 SGK trang 28, 29 tập 1 file word, pdf hoàn toàn miễn phí.