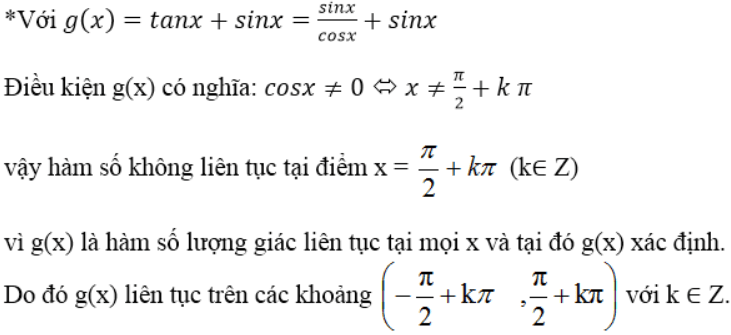Giải toán lớp 11 trang 140, 141 SGK tập 1: Hàm số liên tục

Giải bài tập Toán lớp 11: Hàm số liên tục, nội dung tài liệu bao gồm 6 bài tập trang 140, 141 SGK kèm theo lời giải chi tiết sẽ là nguồn thông tin hay để giúp các bạn học sinh có kết quả cao hơn trong học tập.

Giải bài 1 trang 140 SGK đại số lớp 11

Dùng định nghĩa xét tính liên tục của hàm số f(x) = x³+2x-1 tại x₀=3.

Lời giải:

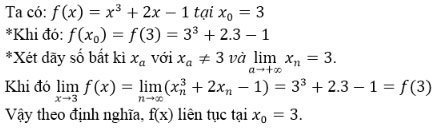
Giải bài 2 lớp 11 đại số trang 141 SGK

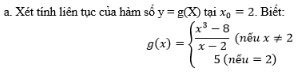
b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x₀=2.

Lời giải:

Giải bài 3 đại số lớp 11 SGK trang 141

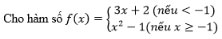
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm sso trên tập xác định của nó.

b. Khẳng định nhận xét trên bằng 1 chứng minh.

Lời giải:

a. Đồ thị hàm số (hình bên). Từ đồ thị ta thấy số gián đoạn tại x = -1.

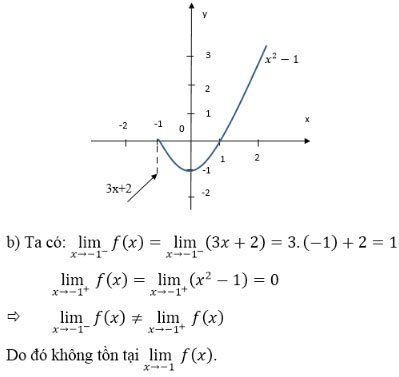
Giải bài 4 đại số lớp 11 trang 141 SGK

Cho các hàm số 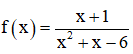 và g(x) = tan(x) + sin(x)

Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.

Lời giải:

Giải bài 5 SGK trang 141 đại số lớp 11

Ý kiến sau đúng hay sai?

"Nếu hàm số y = f(x) liên tục tại điểm x0 và hàm số y = g(x) không liên tục tại x0, thì y = f(x) + g(x) là một hàm số không liên tục tại x₀".

Lời giải:

Ý kiến trên đúng, vì y = h(x) = f(x) + g(x) liên tục tại x₀ thì h(x) – f(x) = g(x) liên tục tại x₀ (theo định lý 2 về hàm số liên tục) trái với giả thiết g(x) không liên tục tại x₀.

Giải bài 6 SGK đại số lớp 11 trang 141

Chứng minh rằng phương trình:

a. 2x³ – 6x + 1 = 0 có ít nhất hai nghiệm.

b. cos x = x có nghiệm

Lời giải:

a. Đặt f(x) = 2x³ – 6x + 1

TXĐ: D = R

Ta có: f(-2) = 2.(-2)³ – 6(-2) + 1 = - 3 < 0

f(-1) = - 2 + 6 + 1 = 5 > 0

f(-2).f(-1) < 0

Mà f(x) là hàm đa thức xác định trên R nên liên tục trên tập R. Do đó f(x) liên tục trên (-2; -1).

Phương trình f(x) = 0 có ít nhất một nghiệm x₀ ∈(-2; -1).

Tương tự ta có:

f(-1) = 2(-1)³ – 6(-1) + 1 = 5

f(1) = 2 - 6 + 1 = -3

f(-1).f(1) < 0 nên phương trình có ít nhất một nghiệm x₀ ∈ (-1;1).

Vì các đoạn (-2; -1) và (-1; 1) rời nhau nên các nghiệm nói trên không thể trùng nhau. Vậy phương trình đã cho có ít nhất 2 nghiệm.

b. Xét hàm số g(x) = x - cos x liên tục trên R, do đó liên tục trên đoạn [- π; π] ta có:

g(- π) = - π - cos (- π) = - π + 1 < 0

g( π) = π - cos π = π - (-1) = π + 1 > 0

g(- π). g( π) <0

Theo định lí 3, phương trình x - cos x = 0 có nghiệm trong (- π; π) tức là cos x = x có nghiệm.

CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải bài Toán lớp 11 SGK tập 1 trang 140, 141 file word, pdf hoàn toàn miễn phí.