Giải Toán 12 Bài 4: Hàm số mũ và Hàm số Lôgarit

Series các bài giải hệ thống bài tập trong sách giáo khoa và sách bài tập Toán lớp 12, hỗ trợ các em tiết kiệm thời gian ôn luyện đạt hiệu quả nhất thông qua các phương pháp giải các dạng toán hay, nhanh và chính xác nhất. Dưới đây là lời giải bài tập SGK Bài 4: Hàm số mũ và hàm số lôgarit từ đội ngũ chuyên gia giàu kinh nghiệm biên soạn và chia sẻ.

Giải Bài 4: Hàm số mũ. Hàm số lôgarit 

Trả lời câu hỏi SGK Toán Giải tích 12 Bài 4:

Trả lời câu hỏi Toán 12 Giải tích Bài 4 trang 71: 

Cho biết năm 2003, Việt Nam có 80902400 người và tỉ lệ tăng dân số là 1,47%. Hỏi năm 2010 Việt Nam sẽ có bao nhiêu người, nếu tỉ lệ tăng dân số hằng năm không đổi ?

Lời giải:

Từ năm 2003 đến năm 2010 là 7 năm.

Vậy năm 2010 Việt Nam sẽ có số người là: 80902400.(1 + 0.0147)⁷ = 89603511,14.

Trả lời câu hỏi Toán 12 Giải tích Bài 4 trang 71: 

Trong các hàm số sau đây, hàm số nào là hàm số mũ ? Với cơ số bao nhiêu ?

a) y = (√3)^x;

b) y = 5^x/3;

c) y = x^-4;

d) y = 4^-x.

Lời giải:

Các hàm số mũ là y = (√3)^x với cơ số là √3, y = 5^x/3 với số mũ là 5^1/3, y = 4^-x với cơ số là 4^-1.

Trả lời câu hỏi Toán 12 Giải tích Bài 4 trang 75: 

Tìm đạo hàm của hàm số y = ln(x + √(1+ x^2 )).

Lời giải:

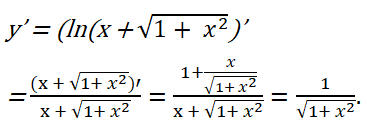
Trả lời câu hỏi Toán 12 Giải tích Bài 4 trang 77: 

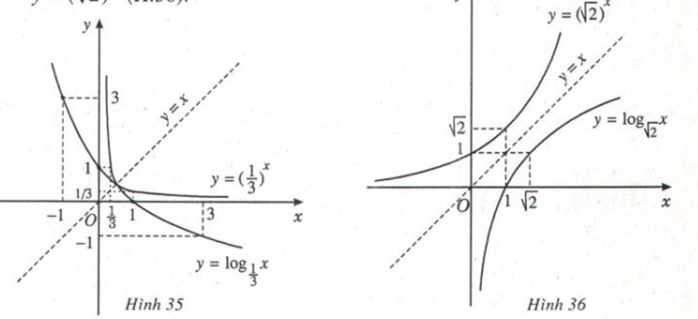
Nêu nhận xét về mối liên hệ giữa đồ thị của các hàm số trên Hình 35 và Hình 36.

Lời giải:

Giải bài tập SGK Toán Giải tích 12 Bài 4:

Bài 1 (trang 77 SGK Giải tích 12): 

Vẽ đồ thị của các hàm số:

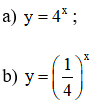
Lời giải:

a) Hàm số y = 4^x

- Tập xác định: D = R.

- Sự biến thiên:

+ y' = 4^x.ln4 > 0 ∀ x ∈ R.

⇒ Hàm số đồng biến trên R.

⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.

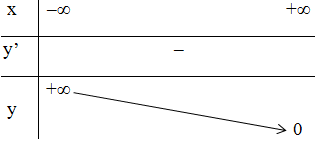
+ Bảng biến thiên:

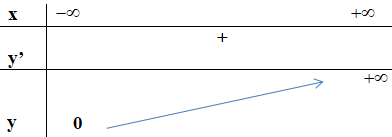
- Đồ thị:

+ Đồ thị hàm số đi qua (0; 1) và (1; 4).

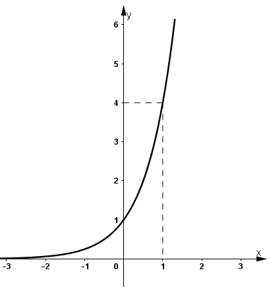
b) Hàm số 

- Tập xác định: D = R.

- Sự biến thiên:

⇒ Hàm số nghịch biến trên R.

⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.

+ Bảng biến thiên:

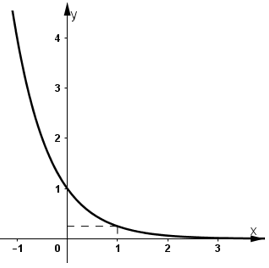
- Đồ thị hàm số:

+ Đồ thị hàm số đi qua (0; 1) và 

Bài 2 (trang 77 SGK Giải tích 12): 

Tính đạo hàm

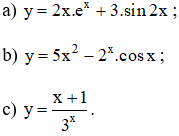
Lời giải:

 

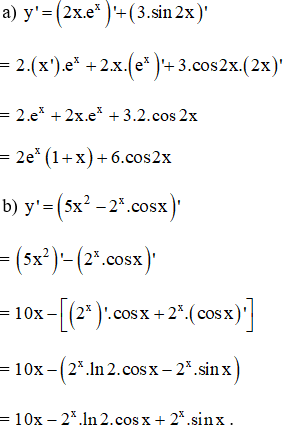
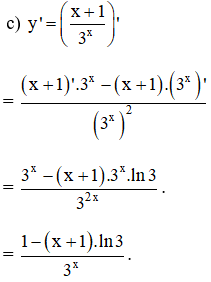
Bài 3 (trang 77 SGK Giải tích 12): 

Tìm tập xác định của các hàm số:

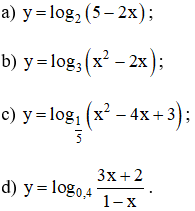
Lời giải:

a) Hàm số y = log₂(5 - 2x) xác định

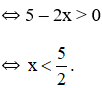
Vậy tập xác định của hàm số là 

b) Hàm số y = log₃(x² - 2x) xác định

⇔ x² – 2x > 0

⇔ x(x – 2) > 0

⇔ x < 0 hoặc x > 2.

Vậy tập xác định của hàm số là D = (-∞; 0) ∪ (2; +∞)

c) Hàm số 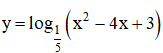 xác định

⇔ x² – 4x + 3 > 0

⇔ (x – 1)(x – 3) > 0

⇔ x > 3 hoặc x < 1.

Vậy tập xác định của hàm số là D = (-∞; 1) ∪ (3; +∞)

d) Hàm số 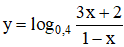 xác định

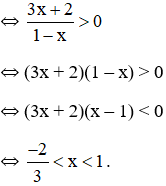
Vậy tập xác định của hàm số là:

Bài 4 (trang 78 SGK Giải tích 12): 

Vẽ đồ thị của các hàm số:

Lời giải:

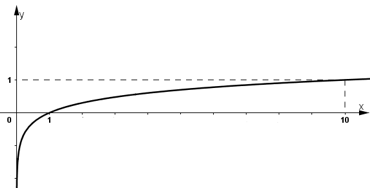
a) Hàm số y = logx

- Tập xác định: D = (0; +∞).

- Chiều biến thiên:

+ Đạo hàm:

⇒ Hàm số đồng biến trên D.

⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số.

+ Bảng biến thiên:

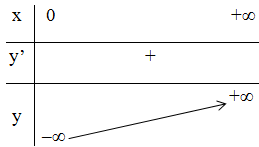
- Đồ thị hàm số:

+ Đồ thị hàm số đi qua (1; 0) và (10; 1).

b) Hàm số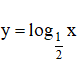 

- Tập xác định: D = (0; +∞).

- Chiều biến thiên:

+ Đạo hàm:

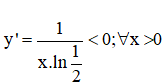
⇒ Hàm số nghịch biến trên D.

⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số.

+ Bảng biến thiên:

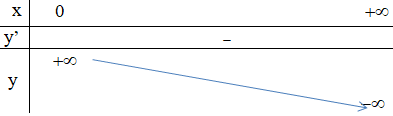
- Đồ thị:

+ Đồ thị hàm số đi qua (1; 0) và (1/2; 1).

Bài 5 (trang 78 SGK Giải tích 12): 

Tính đạo hàm của các hàm số

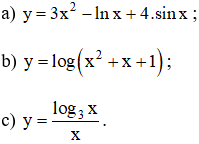
Lời giải:

 

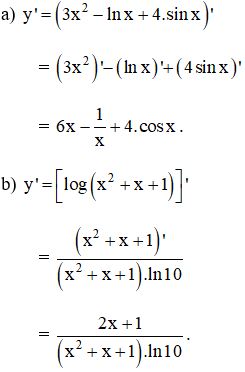
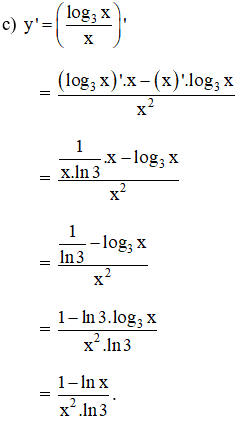
Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập SGK Toán 12 về bất phương trình mũ và logarit file Word, pdf hoàn toàn miễn phí!