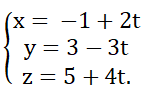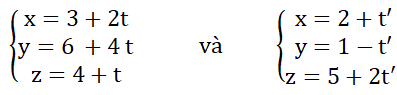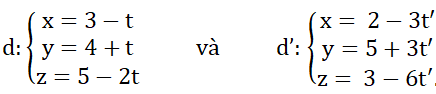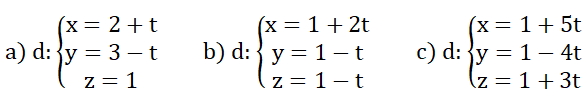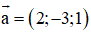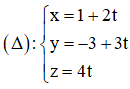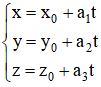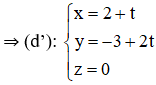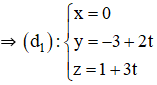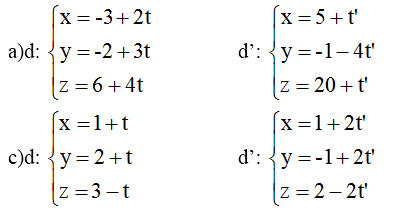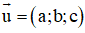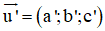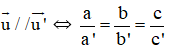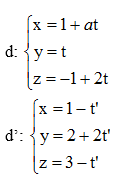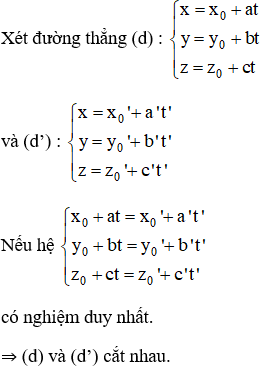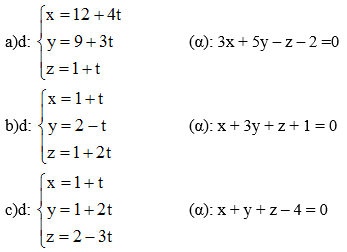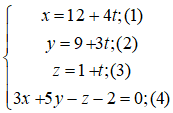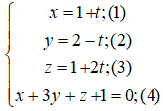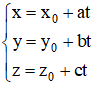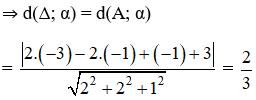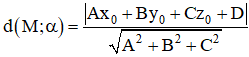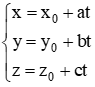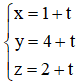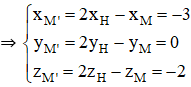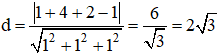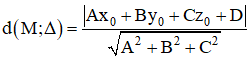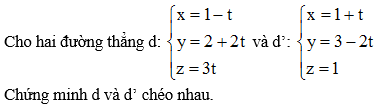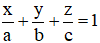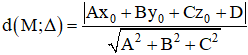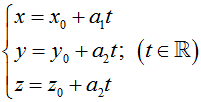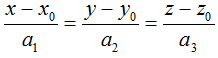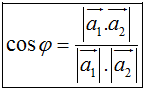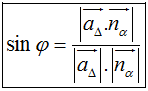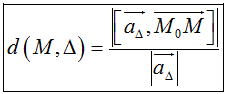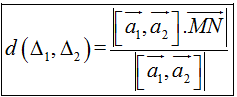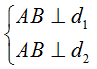Giải Toán Hình lớp 12 Bài 3: Phương trình đường thẳng trong không gian trang 82, 84, 86, 89, 90, 91

Mời các em học sinh và quý thầy cô tham khảo hướng dẫn Giải Toán Hình 12 Bài 3: Phương trình đường thẳng trong không gian trang 82, 84, 86, 89, 90, 91 chính xác nhất, được đội ngũ chuyên gia biên soạn đầy đủ và ngắn gọn dưới đây.

Giải bài tập Toán Hình 12 Bài 3: Phương trình đường thẳng trong không gian

Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 82: Trong không gian Oxyz cho điểm M_o(1; 2; 3) và hai điểm M₁(1 + t; 2 + t; 3 + t), M₂(1 + 2t; 2 + 2t; 3 + 2t) di động với tham số t. Hãy chứng tỏ ba điểm M_o,M₁,M₂ luôn thẳng hàng.

Lời giải:

M_oM₁→ = (t;t;t); M_oM₂→ = (2t;2t;2t)

⇒ M_oM₂→ = 2M_oM₁→ ⇒ M_oM₁→ và M_oM₂→ cùng phương

⇒ ba điểm M_o, M₁, M₂ luôn thẳng hàng

Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 84: Cho đường thẳng Δ có phương trình tham số

Hãy tìm tọa độ của một điểm M trên Δ và tọa độ một vecto chỉ phương của Δ.

Lời giải:

1 điểm M thuộc Δ là: M (-1; 3; 5) và 1 vecto chỉ phương của Δ là a→ = (2;-3;4)

Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 84: Cho hai đường thẳng d và d' có phương trình tham số lần lượt là

a) Hãy chứng tỏ điểm M(1; 2; 3) là điểm chung của d và d’;

b) Hãy chứng tỏ d và d’ có hai vecto chỉ phương không cùng phương.

Lời giải:

a) tọa độ M thỏa mãn phương trình tham số của d với t = -1

Tọa độ M thỏa mãn phương trình tham số của d’ với t = -1

⇒ M là điểm chung của d và d’

b) a_d→ = (2;4;1); a_d'→ = (1;-1;2) là hai vecto không tỉ lệ nên hai veco đó không cùng phương

Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 86: Chứng minh hai đường thẳng sau đây trùng nhau:

Lời giải:

a_d→ = (-1;1;-2); a_d'→ = (-3;3;-6) ⇒ a_d'→ = 3a_d→

M (3; 4; 5) ∈ d và M (3; 4; 5) ∈ d’

Nên d trùng với d’

Trả lời câu hỏi Toán 12 Hình học Bài 3 trang 89: Tìm số giao điểm của mặt phẳng (α): x + y + z - 3 = 0 với đường thẳng d trong các trường hợp sau:

Lời giải:

a) Xét phương trình: (2 + t) + (3 - t) + 1 – 3 = 0

⇔ 3 = 0(vô nghiệm) ⇒ mặt phẳng (α)và d không có điểm chung

b) Xét phương trình: (1 + 2t) + (1 - t) + (1 - t) – 3 = 0

⇔ 0 = 0(vô số nghiệm) ⇒ d ∈ (α)

c) Xét phương trình: (1 + 5t) + (1 - 4t) + (1 + 3t) – 3 = 0

⇔ 4t = 0 ⇔ t = 0 ⇒ mặt phẳng (α)và d có 1 điểm chung

Bài 1 (trang 89 SGK Hình học 12): Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau:

a) d đi qua M(5; 4; 1) và có vectơ chỉ phương 

b) d đi qua A(2; -1; 3) và vuông góc với mặt phẳng (α): x + y – z + 5 = 0.

c) d đi qua B(2; 0; -3) và song song với đường thẳng 

d) d đi qua hai điểm P(1; 2; 3) và Q(5; 4; 4).

Lời giải:

Kiến thức áp dụng

+ Phương trình tham số của đường thẳng (d) có vectơ chỉ phương 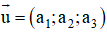 và đi qua M(x₀; y₀; z₀) là:

+ Hai đường thẳng (d) và (d’) song song nếu hai vec tơ chỉ phương 

Bài 2 (trang 89 SGK Hình học 12): Viết phương trình tham số của đường thẳng là hình chiếu vuông góc của đường thẳng

Lời giải:

+ t = 0 ⇒ điểm M(2; -3; 1) ∈ d

+ t = 1 ⇒ điểm N(3; -1; 4) ∈ d.

a) Hình chiếu của M trên (Oxy) là M’(2 ; -3 ; 0).

Hình chiếu của N trên (Oxy) là : N’(3 ; -1 ; 0).

⇒ Hình chiếu của d trên (Oxy) chính là đường thẳng d’ đi qua M’ và N’.

⇒ d’ nhận 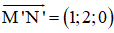 là 1 vtcp.

b) Hình chiếu của M trên (Oyz) là : M₁(0 ; -3 ; 1)

Hình chiếu của N trên (Oyz) là : N₁(0 ; -1 ; 4)

⇒ Hình chiếu của d trên (Oyz) chính là đường thẳng d₁ đi qua M₁ và N₁

⇒ d1 nhận 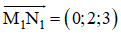 là 1 vtcp

Kiến thức áp dụng

+ Các điểm thuộc đường thẳng (d): 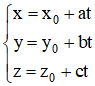 đều có dạng M(x₀ + at; y₀ + bt; z₀ + ct)

+ Hình chiếu của M(x₀; y₀ ; z₀) trên (Oxy) là: M₁(x₀ ; y₀ ; 0)

trên (Oyz) là : M₂(0 ; y₀ ; z₀)

trên (Ozx) là : M₃(x₀ ; 0 ; z₀).

Bài 3 (trang 90 SGK Hình học 12): Xét vị trí tương đối các cặp đường thẳng d và d' cho bởi các phương trình sau:

Lời giải:

Kiến thức áp dụng

Xét đường thẳng (d) : 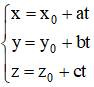 có vtcp 

và (d’) : 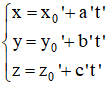 có vtcp 

+ TH1 : 

+ TH2: u→ không song song với u'→:

Nếu hệ 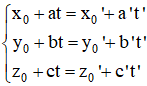 có nghiệm duy nhất.

⇒ (d) và (d’) cắt nhau.

Nếu hệ 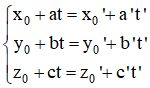 vô nghiệm

⇒ (d) và (d’) chéo nhau.

Bài 4 (trang 90 SGK Hình học 12): Tìm a để hai đường thẳng sau đây cắt nhau:

Lời giải:

Kiến thức áp dụng

Bài 5 (trang 90 SGK Hình học 12): Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:

Lời giải:

a) Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:

Thay (1); (2); (3) vào (4) ta được:

3(12 + 4t) + 5(9 + 3t) – (1 + t) – 2 = 0

⇔ 36 + 12t + 45 + 15t – 1 – t – 2 = 0

⇔ 26t + 78 = 0

⇔ t = -3

Vậy (d) cắt (α) tại một điểm M(0 ; 0 ; -2).

b) Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:

Thay (1); (2); (3) vào (4) ta được:

1 + t + 3(2 – t) + 1 + 2t + 1 = 0

⇔ 0t + 9 = 0

Phương trình vô nghiệm

⇒ (d) không cắt (α).

c) Giao điểm (nếu có) của đường thẳng (d) và mp(α) là nghiệm hệ phương trình:

Thay (1); (2); (3) vào (4) ta được:

1 + t + 1 + 2t + 2 – 3t – 4 = 0

⇔ 0t = 0

Phương trình có vô số nghiệm

⇒ (d) ⊂ (α)

hay (d) cắt (α) tại vô số điểm.

Kiến thức áp dụng

+ Trong không gian Oxyz, cho mặt phẳng (α): Ax + By + Cz + D = 0 và đường thẳng d: 

Xét phương trình A(x₀ + at) + B(y₀ + bt) + C(z₀ + ct) + D = 0 (1)

+ Nếu (1) vô nghiệm ⇒ (d) không có điểm chung với (α) ⇒ d // (α).

+ Nếu (1) có 1 nghiệm t = t₀ thì (d) cắt (α) tại M (x₀ + at₀; y₀ + bt₀; z₀ + ct₀).

+ Nếu (1) có vô số nghiệm thì (d) thuộc (α).

Bài 6 (trang 90 SGK Hình học 12): Tính khoảng cách giữa đường thẳng ...

Lời giải:

Xét phương trình:

2(-3 + 2t) – 2(-1 + 3t) + (-1 + 2t) + 3 = 0

⇔ 0t – 2 = 0

Phương trình vô nghiệm

⇒ (Δ) // (α).

Điểm A(-3; -1; -1) ∈ (Δ).

Kiến thức áp dụng

+ Trong không gian Oxyz, cho mặt phẳng (α): Ax + By + Cz + D = 0 và đường thẳng d: 

Xét phương trình A(x₀ + at) + B(y₀ + bt) + C(z₀ + ct) + D = 0 (1)

+ Nếu (1) vô nghiệm ⇒ (d) không có điểm chung với (α) ⇒ d // (α).

+ Khoảng cách từ điểm M(x₀; y₀; z₀) đến (α) là:

Bài 7 (trang 91 SGK Hình học 12): Cho điểm A(1; 0; 0) và đường thẳng ...

Lời giải:

Kiến thức áp dụng

Cách tìm hình chiếu H của điểm M trên đường thẳng (Δ): 

Cách 1:

+ Tham số hóa tọa độ điểm H(x₀ + at; y₀ + bt; z₀ + ct).

Từ 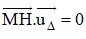 ⇒ tìm được t

⇒ Thay vào tọa độ điểm H ta tìm được hình chiếu của M trên (Δ).

Cách 2:

Viết phương trình mặt phẳng (α) đi qua M và vuông góc với đường thẳng (Δ)

⇒ (α) nhận 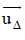 là 1 vtpt

Hình chiếu H chính là giao điểm của đường thẳng (Δ) và mặt phẳng (α).

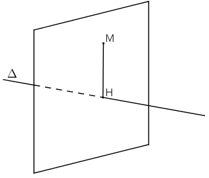
Bài 8 (trang 91 SGK Hình học 12): Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0

a)Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).

b)Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).

c)Tính khoảng cách từ M đến mp(α).

Lời giải:

a) Đường thẳng MH vuông góc với (α)

⇒ MH nhận vtpt của (α) 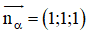 là 1 vtcp

Mà M(1; 4; 2) ∈ MH

⇒ Pt đường thẳng MH: 

⇒ H(1 + t; 4 + t; 2 + t).

H ∈ (α) ⇒ 1 + t + 4 + t + 2 + t – 1 = 0 ⇔ t = -2.

⇒ H(-1; 2; 0).

b) M’ đối xứng với M qua (α)

⇒ H là trung điểm MM’

⇒ M’(-3; 0; -2).

c) Khoảng cách từ M đến mặt phẳng (α) là:

Kiến thức áp dụng

+ Tìm hình chiếu H của điểm M trên mặt phẳng (Δ): Ax + By + Cz + D = 0

Phương trình đường thẳng MH đi qua M và vuông góc với Δ

⇒ MH nhận vtpt của Δ là (A; B; C) là 1 vtpt

⇒ viết phương trình MH.

⇒ tìm tọa độ H là giao điểm của MH và (Δ).

+ Khoảng cách từ M(x0 ; y0 ; z0) đến (Δ): Ax + By + Cz + D = 0

Bài 9 (trang 91 SGK Hình học 12): Cho hai đường thẳng d:

Lời giải:

Kiến thức áp dụng

Xét đường thẳng (d) : 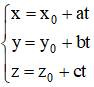 có vtcp 

và (d’) : 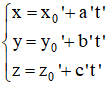 có vtcp 

+ TH1 : 

+ TH2: u→ không song song với u'→:

Nếu hệ 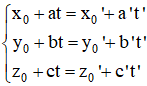 có nghiệm duy nhất.

⇒ (d) và (d’) cắt nhau.

Nếu hệ 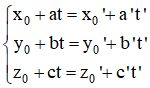 vô nghiệm

⇒ (d) và (d’) chéo nhau.

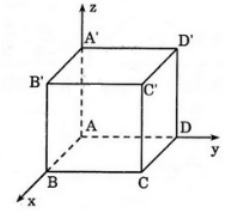
Bài 10 (trang 91 SGK Hình học 12): Giải bài toán sau đây bằng phương pháp tọa độ. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính khoảng cách từ đỉnh A đến các mặt phẳng (A'BD) và (B'D'C).

Lời giải:

Kiến thức áp dụng

+ Phương trình đoạn chắn của mặt phẳng cắt các trục Ox ; Oy ; Oz lần lượt tại (a ; 0 ; 0) ; (0 ; b ; 0) ; (0 ; 0 ; c) là : 

+ Khoảng cách từ M(x0 ; y0 ; z0) đến (Δ): Ax + By + Cz + D = 0

Lý thuyết Toán Hình lớp 12 Bài 3: Phương trình đường thẳng trong không gian

A. Tóm tắt lý thuyết

I. Phương trình đường thẳng:

    • Cho đường thẳng Δ đi qua điểm M_o(x_o; y_o; z_o) và nhận vectơ a→ = (a₁; a₂; a₃) với a₁² + a₂² + a₃² ≠ 0 làm vectơ chỉ phương. Khi đó Δ có phương trình tham số là :

    • Cho đường thẳng Δ đi qua điểm M_o(x_o; y_o; z_o) và nhận vectơ a→ = (a₁; a₂; a₃) sao cho a₁a₂a₃ ≠ 0 làm vectơ chỉ phương. Khi đó Δ có phương trình chính tắc là :

II. Góc:

1. Góc giữa hai đường thẳng:

    Δ₁ có vectơ chỉ phương a₁→

    Δ₂ có vectơ chỉ phương a₂→

    Gọi φ là góc giữa hai đường thẳng Δ₁ và Δ₂. Ta có:

2. Góc giữa đường thẳng và mặt phẳng:

    Δ có vectơ chỉ phương a_Δ→

    (α) có vectơ chỉ phương n_α→

    Gọi φ là góc giữa hai đường thẳng Δ và α. Ta có:

III. Khoảng cách:

1. Khoảng cách từ điểm M đến đường thẳng Δ:

    Δ đi qua điểm M_o và có vectơ chỉ phương a_Δ→

2. Khoảng cách giữa hai đường thẳng chéo nhau:

    Δ₁ đi qua điểm M và có vectơ chỉ phươnga₁→

    Δ₂ đi qua điểm N và có vectơ chỉ phương a₂→

B. Kĩ năng giải bài tập

    Các dạng toán thường gặp

    1. Viết phương trình đường thẳng Δ đi qua hai điểm phân biệt A, B.

    Cách giải:

    Xác định vectơ chỉ phương của Δ là AB→.

    2. Đường thẳng Δ đi qua điểm M và song song với d.

    Cách giải:

    Trong trường hợp đặc biệt:

    • Nếu Δ song song hoặc trùng bới trục Ox thì Δ có vectơ chỉ phương là a_Δ→ = i→ = (1; 0; 0)

    • Nếu Δ song song hoặc trùng bới trục Oy thì Δ có vectơ chỉ phương là a_Δ→ = j→ = (0; 1; 0)

    • Nếu Δ song song hoặc trùng bới trục Oz thì Δ có vectơ chỉ phương là a_Δ→ = k→ = (0; 1; 0)

    Các trường hợp khác thì Δ có vectơ chỉ phương là a_Δ→ = a_d→, với a_d→ là vectơ chỉ phương của d

    3. Viết phương trình đường thẳng Δ đi qua điểm M và vuông góc với mặt phẳng (α).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = n_α→, với n_α→ là vectơ pháp tuyến của (α).

    4. Viết phương trình đường thẳng Δ đi qua điểm M và vuông góc với hai đường thẳng d₁, d₂ (hai đường thẳng không cùng phương).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = [a₁→, a₂], với a₁→, a₂→ lần lượt là vectơ chỉ phương của d₁, d₂.

    5. Viết phương trình đường thẳng Δ đi qua điểm M vuông góc với đường thẳng d và song song với mặt phẳng (α).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_α→ = [a_d→, n_α→], với a_d→ là vectơ chỉ phương của d, n_α→ là vectơ pháp tuyến của (α).

    6. Viết phương trình đường thẳng Δ đi qua điểm A và song song với hai mặt phẳng (α), (β); ((α), (β) là hai mặt phẳng cắt nhau)

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = [n_α→, n_β→], với n_α→, n_β→ lần lượt là vectơ pháp tuyến của (α), (β).

    7. Viết phương trình đường thẳng Δ là giao tuyến của hai mặt phẳng (α) và (β).

    Cách giải:

    • Lấy một điểm bất kì trên Δ, bằng cách cho một ẩn bằng một số tùy ý.

    • Xác định vectơ chỉ phương của Δ là a_Δ→ = [n_α→, n_β→], với n_α→, n_β→ lần lượt là vectơ pháp tuyến của (α), (β).

    8. Viết phương trình đường thẳng Δ đi qua điểm A và cắt hai đường thẳng d₁, d₂ (A ∉ d₁, A ∉ d₂).

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = [n₁→, n₂→], với n₁→, n₂→ lần lượt là vectơ pháp tuyến của mp(A, d₁), mp(A, d₂).

    9. Viết phương trình đường thẳng Δ nằm trong mặt phẳng (α) và cắt hai đường thẳng d₁, d₂.

    Cách giải:

    Xác định vectơ chỉ phương của Δ là a_Δ→ = AB→, với A = d₁ ∩ (α), B = d₂ ∩ (α)

    10. Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc và cắt d.

    Cách giải:

    • Xác định B = Δ ∩ d.

    • Viết phương trình đường thẳng Δ đi qua A, B.

    11. Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với d₁ và cắt d₂, với A ∉ d₂.

    Cách giải:

    • Xác định B = Δ ∩ d₂.

    • Viết phương trình đường thẳng Δ đi qua A, B.

    12. Viết phương trình đường thẳng Δ đi qua điểm A, cắt đường thẳng d và song song với mặt phẳng (α).

    Cách giải:

    • Xác định B = Δ ∩ d.

    • Viết phương trình đường thẳng Δ đi qua A, B.

    13. Viết phương trình đường thẳng Δ nằm trong mặt phẳng (α) cắt và vuông góc đường thẳng d.

    Cách giải:

    • Xác định A = d ∩ (α).

    • Đường thẳng Δ đi qua A và có vectơ chỉ phương của Δ là a_Δ→ = [a_d→, n_α→], với a_d→ là vectơ chỉ phương của d, n_α→ là vectơ pháp tuyến của (α).

    14. Viết phương trình đường thẳng Δ đi qua giao điểm A của đường thẳng d và mặt phẳng (α), nằm trong (α) và vuông góc đường thẳng d (ở đây d không vuông góc với (α)) .

    Cách giải:

    • Xác định A = d ∩ (α).

    • Đường thẳng Δ đi qua A và có vectơ chỉ phương của Δ là a_Δ→ = [a_d→, n_α→], với a_d→ là vectơ chỉ phương của d, n_α→ là vectơ pháp tuyến của (α).

    15. Viết phương trình đường thẳng Δ là đường vuông góc chung của hai đường thẳng chéo nhau d₁, d₂.

    Cách giải:

    • Xác định A = Δ ∩ d₁, B = Δ ∩ d₂ sao cho 

    • Viết phương trình đường thẳng Δ đi qua hai điểm A, B.

    16. Viết phương trình đường thẳng Δ song song với đường thẳng d và cắt cả hai đường thẳng d₁, d₂.

    Cách giải:

    • Xác định A = Δ ∩ d₁, B = Δ ∩ d₂ sao cho AB→, a_d→ cùng phương, với a_d→ là vectơ chỉ phương của d.

    • Viết phương trình đường thẳng Δ đi qua điểm A và có vectơ chỉ phương a_d→ = a_α→.

    17. Viết phương trình đường thẳng Δ vuông góc với mặt phẳng (α) và cắt cả hai đường thẳng d₁, d₂.

    Cách giải:

    • Xác định A = Δ ∩ d₁, B = Δ ∩ d₂ sao cho AB→, n_α→ cùng phương, với n_α→ là vectơ pháp tuyến của (α).

    • Viết phương trình đường thẳng Δ đi qua điểm A và có vectơ chỉ phương a_d→ = n_α→.

    18. Viết phương trình Δ là hình chiếu vuông góc của d lên mặt phẳng (α).

    Cách giải :

    Xác định H ∈ Δ sao cho AH→ ⊥ a_d→,với a_d là vectơ chỉ phương của d.

    • Viết phương trình mặt phẳng (β) chứa d và vuông góc với mặt phẳng (α).

    • Viết phương trình đường thẳng Δ là giao tuyến của hai mặt phẳng (α) và (β)

    19. Viết phương trình Δ là hình chiếu song song của d lên mặt phẳng (α) theo phương d'.

    Cách giải :

    • Viết phương trình mặt phẳng (β) chứa d và có thêm một véc tơ chỉ phương u_d'→.

    • Viết phương trình đường thẳng Δ là giao tuyến của hai mặt phẳng (α) và (β).

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán Hình lớp 12 Bài 3: Phương trình đường thẳng trong không gian trang 82, 84, 86, 89, 90, 91 file PDF hoàn toàn miễn phí.