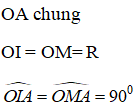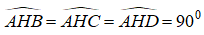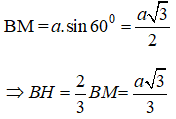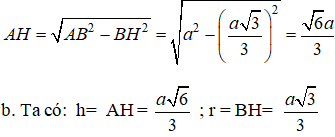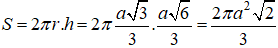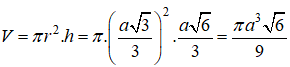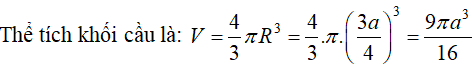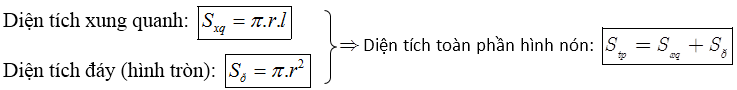Giải Toán Hình lớp 12 Ôn tập chương 2 trang 50

Mời các em học sinh và quý thầy cô tham khảo hướng dẫn Giải Toán Hình 12 Ôn tập chương 2 trang 50 chính xác nhất, được đội ngũ chuyên gia biên soạn đầy đủ và ngắn gọn dưới đây.

Giải bài tập Toán Hình 12 Ôn tập chương 2

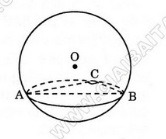
Bài 1 trang 50 SGK Hình học 12: Cho ba điểm A, B, C cùng thuộc một mặt cầu sao cho (ACB)=90^o.Trong các khẳng định sau, khẳng định nào đúng?

a) Đường tròn qua ba điểm A, B, C nằm trên mặt cầu.

b) AB là một đường kính của mặt cầu đã cho.

c) AB không phải là đường kính của mặt cầu.

d) AB là đường kính của đường tròn giao tuyến tạo bởi mặt cầu và mặt phẳng (ABC).

Lời giải:

a) Đúng

b) Sai

c) Sai

d) Đúng.

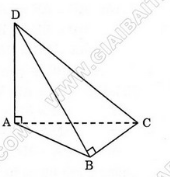
Bài 2 (trang 50 SGK Hình học 12): Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a. Tính diện tích xung quanh của hình nón và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.

Lời giải:

Bài 3 (trang 50 SGK Hình học 12): Một hình chóp có tất cả các cạnh bên bằng nhau. Chứng minh rằng hình chóp đó nội tiếp được trong một mặt cầu (các đỉnh của hình chóp nằm trên mặt cầu).

Lời giải:

Cho hình chóp S.A₁A₂A₃...A_n có các cạnh bên bằng nhau.

Gỉa sử I là hình chiếu vuông góc của S trên mặt đáy.

Ta có: SA₁ = SA₂ = SA₃ = ... = SA_n

Suy ra ΔSIA₁= ΔSIA₂ = ΔSIA₃ = ... = ΔSIA_n

Suy ra IA₁ = IA₂ = IA₃ = ... = IA_n

Đa giác A₁A₂A₃...A_n là một đa giác nội tiếp được trong một đường tròn tâm I bán kính IA, trục SI.

Trong mp(SAI), đường trung trực của SA₁ cắt SI tại O, ta có:

OS = OA₁ (1)

OA₁ = OA₂ = OA₃ = ... = OA_n (2)

Từ (1) và (2) suy ra OS = OA₁ = OA₂ = OA₃ = ... = OA_n

Vậy hình chóp S.A₁A₂A₃...A_n nội tiếp được trong một mặt cầu.

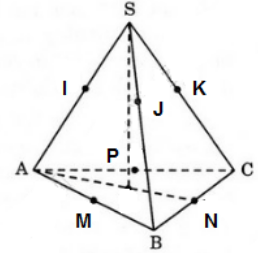
Bài 4 (trang 50 SGK Hình học 12): Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh bên SA, SB, SC. Mặt cầu này còn tiếp xúc với ba cạnh AB, BC, CA tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.

Lời giải:

Gọi mặt cầu đã cho có tâm O và bán kính R.

Gọi M, N, P lần lượt là trung điểm của AB, BC và CA.

Gọi I,J và K lần lượt là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu:

+ Từ giả thiết ta suy ra: OI ⊥ SA; OM ⊥ AB

Xét tam giác OIA và tam giác OMA có:

⇒ ∆ OIA = ∆OMA ( ch- cgv)

⇒ AM = AI.

Chứng minh tương tự có: BM= BJ và SI = SJ (1)

Mà AM = BM nên AI= BJ ; (2)

Từ (1) và (2) suy ra: SI+IA = SJ + BJ hay SA = SB (3)

* Chứng minh tương tự, ta có SB= SC (4).

Từ (3) và (4) suy ra: SA = SB = SC (*)

Mặt khác ; BM = BN (= BJ) và CN = CP (= CK)

Suy ra; AB = 2BM = BC = 2 CN = 2CP = CA

Do đó, tam giác ABC là tam giác đều (**)

Từ (*) và (**) suy ra, S. ABC là hình chóp tam giác đều.

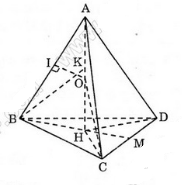
Bài 5 (trang 50 SGK Hình học 12): Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).

a) Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH.

b) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao AH.

Lời giải:

a. Từ A vẽ AH ⊥ (BCD)

Xét ba tam giác ABH, ACH và ADH có:

AB= AC = AD ( vì ABCD là tứ diện đều).

AH chung

=> ∆ ABH = ∆ ACH =∆ ADH ( ch- cgv)

Suy ra,HB = HC = HD . Do đó, H là tâm đường tròn ngoại tiếp tam giác BCD

Do tam giác BCD là tam giác đều nên H đồng thời là trọng tâm tam giác BCD

Gọi M là trung điểm CD. Ta có;

+ xét tam giác AHB vuông tại H có:

Diện tích xung quanh của hình trụ là:

Thể tích của khối trụ là;

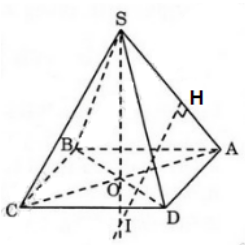
Bài 6 (trang 50 SGK Hình học 12): Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng Δ vuông góc với mặt phẳng (ABCD). Trên Δ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.

Lời giải:

Bài 7 (trang 50 SGK Hình học 12): Cho hình trụ có bán kính r, trục OO' = 2r và mặt cầu đường kính OO'.

a) Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ.

b) Hãy so sánh thể tích khối trụ và thể tích khối cầu được tạo nên bởi hình trụ và mặt cầu đã cho.

Lời giải:

a. Do trục OO’= 2r nên chiều cao của khối trụ là h = 2r.

Mặt cầu có đường kính là OO’= 2r nên bán kính của mặt cầu là: R = r

Lý thuyết Toán Hình lớp 12 Ôn tập chương 2

A. Tóm tắt lý thuyết

** MẶT NÓN

    Cho hình nón có chiều cao là h, bán kính đáy r và đường sinh là l thì có:

    - Thể tích khối nón: .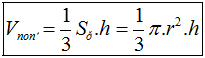

** MẶT TRỤ

    Cho hình trụ có chiều cao là và bán kính đáy bằng r, khi đó:

    - Diện tích xung quanh của hình trụ: S_xq = 2πrh

    - Diện tích toàn phần của hình trụ: S_tp = S_xq + 2.S_Đay = 2πrh + 2πr²

    - Thể tích khối trụ: V = B.h = πr²h

** MẶT CẦU

    • Diện tích mặt cầu: S_C = 4πR².

    • Thể tích mặt cầu: V_C = (4/3)πR³.

** KỸ THUẬT XÁC ĐỊNH MẶT CẦU NGOẠI TIẾP HÌNH CHÓP.

    Bước 1: Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng Δ: trục đường tròn ngoại tiếp đa giác đáy.

    Bước 2: Lập mặt phẳng trung trực (α) của một cạnh bên.

    Lúc đó : - Tâm O của mặt cầu: Δ ∩ mp(α) = {O}

    - Bán kính: R = SA (= SO) . Tuỳ vào từng trường hợp.

    Lưu ý: Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy.

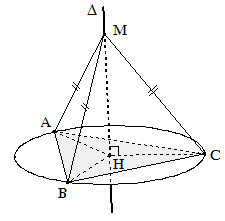
    1. Trục đường tròn ngoại tiếp đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với mặt phẳng đáy.

    Tính chất: ∀M ∈ Δ: MA = MB = MC

    Suy ra: MA = MB = MC ⇔ M ∈ Δ

    2. Các bước xác định trục:

    - Bước 1: Xác định tâm H của đường tròn ngoại tiếp đa giác đáy.

    - Bước 2: Qua H dựng Δ vuông góc với mặt phẳng đáy.

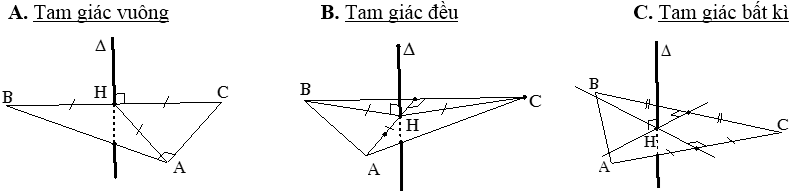
    VD: Một số trường hợp đặc biệt

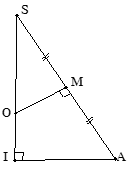
    3. Lưu ý: Kỹ năng tam giác đồng dạng

    ΔSMO đồng dạng với ΔSIA  .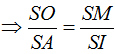

    4. Nhận xét quan trọng:

     ⇒ SM là trục đường tròn ngoại tiếp ΔABC.

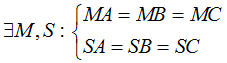
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán Hình lớp 12 Ôn tập chương 2 trang 50 file PDF hoàn toàn miễn phí.