Giải bài tập Toán 12: Ôn tập chương 1 (Phần Đại số)

Tích cực giải các bài tập phần ôn tập sau khi kết thúc mỗi chương giúp các em tổng hợp lại kiến thức lý thuyết đã học và ứng dụng chúng vào các bài tập thực tế, từ đó nắm sâu kiến thức, linh hoạt trong việc giải các bài tập ở mức độ khó hơn nhằm đạt kết quả cao nhất trong kì thi quan trọng sắp tới.

Giải bài: Ôn tập chương 1 Giải tích 12

Bài 1 (trang 45 SGK Giải tích 12): 

Phát biểu các điều kiện đồng biến và nghịch biến của hàm số. Tìm các khoảng đơn điệu của hàm số

y = -x³ + 2x² - x - 7;

Lời giải:

- Điều kiện đồng biến, nghịch biến của hàm số:

Cho hàm số y = f(x) có đạo hàm trên khoảng K.

+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.

+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.

- Xét hàm số y = -x³ + 2x² - x - 7, ta có:

y' = -3x² + 4x – 1

+ Hàm số đồng biến

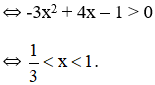
+ Hàm số nghịch biến

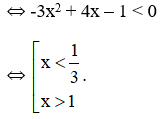
Vậy hàm số đồng biến trên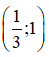 

nghịch biến trên các khoảng 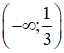 và (1; +∞)

- Xét hàm số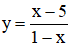 

Ta có: D = R \ {1}

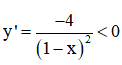 ∀ x ∈ D.

⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).

Bài 2 (trang 45 SGK Giải tích 12): 

Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số:

y = x⁴ - 2x² + 2

Lời giải:

a) Cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:

Quy tắc 1:

1. Tìm tập xác định.

2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2:

1. Tìm tập xác định.

2. Tính f'(x). Giải phương trình f'(x) = 0 và kí hiệu x_i (i = 1, 2, 3, ...) là các nghiệm của nó.

3. Tính f"(x) và f"(x_i)

4. Nếu f"(x_i) > 0 thì x_i là điểm cực tiểu.

Nếu f"(x_i) < 0 thì x_i là điểm cực đại.

b) Xét hàm số y = x⁴ - 2x² + 2, ta có:

y' = 4x³ - 4x = 4x(x² - 1)

y' = 0 ⇔ 4x(x² - 1) = 0 ⇔ x = 0; x = ±1

y" = 12x² - 4

Dựa vào Quy tắc 2, ta có:

y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại.

y"(-1) = y"(1) = 8 > 0 ⇒ x = ±1 là hai điểm cực tiểu.

Bài 3 (trang 45 SGK Giải tích 12): 

Nêu cách tìm ra tiệm cận ngang và tiệm cận dứng của đồ thị hàm số. Áp dụng để tìm các tiệm cận của đồ thị hàm số:

Áp dụng để tìm các tiệm cận của đồ thị hàm số 

Lời giải:

a) - Cách tìm tiệm cận ngang:

+ Tính các giới hạn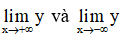 

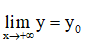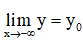+ Nếu  hoặc  thì y = y₀ là tiệm cận ngang của đồ thị hàm số.

- Cách tìm tiệm cận đứng:

Đường thẳng x = x₀ là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

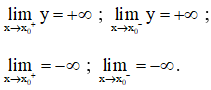
b) Xét hàm số: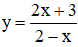

⇒ Đồ thị có tiệm cận đứng là x = 2.

⇒ Đồ thị có tiệm cận ngang là y = -2.

Bài 4 (trang 45 SGK Giải tích 12): 

Nhắc lại sơ đồ khảo sát sự biến thiên và vẽ đồ thị của hàm số.

Lời giải:

Hàm số y = f(x)

Các bước khảo sát hàm số:

1. Tìm tập xác định của hàm số

2. Sự biến thiên

- Xét chiều biến thiên:

   + Tính đạo hàm y'

   + Tìm các điểm tại đó y' bằng 0 hoặc không xác định

   + Xét dấu của đạo hàm y' và suy ra chiều biến thiên của hàm số.

- Tìm cực trị

- Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận (nếu có)

- Lập bảng biến thiên.

3. Vẽ đồ thị của hàm số

Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị.

Bài 5 (trang 45 SGK Giải tích 12): 

Cho hàm số y = 2x² + 2mx + m - 1 có đồ thị là (C_m), m là tham số.

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = -1

b) Xác định m để hàm số:

    i) Đồng biến trên khoảng (-1; +∞)

    ii) Có cực trị trên khoảng (-1; +∞)

c) Chứng minh rằng (C_m) luôn cắt trục hoành tại hai điểm phân biệt với mọi m.

Lời giải:

a) Với m = 1 ta được hàm số: y = 2x² + 2x

- TXĐ: D = R,

- Sự biến thiên:

+ Chiều biến thiên: y' = 4x + 2

y' = 0 ⇔ x = -1/2

+ Bảng biến thiên:

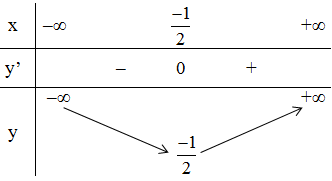
Kết luận: Hàm số nghịch biến trên (-∞; -1/2), đồng biến trên (-1/2; +∞).

Đồ thị hàm số có điểm cực tiểu là (-1/2; -1/2)

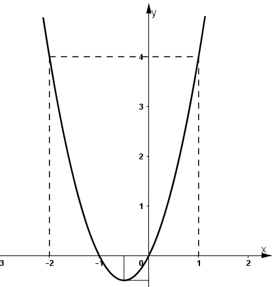
- Đồ thị:

Ta có: 2x² + 2x = 0 ⇔ 2x(x + 1) = 0

⇒ x = 0; x = -1

+ Giao với Ox: (0; 0); (-1; 0)

+ Giao với Oy: (0; 0)

b) Xét hàm số y = 2x² + 2mx + m - 1

y' = 4x + 2m = 2(2x + m)

y' = 0 ⇒ x = -m/2

Ta có bảng xét biến thiên :

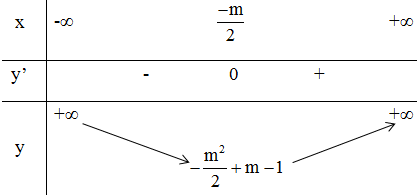
Từ bảng biến thiên ta thấy :

- Hàm số đồng biến trên khoảng (-1; +∞)

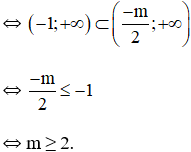
- Hàm số có cực trị trên khoảng (-1; +∞)

c) Nhận thấy: 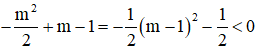 với mọi m.

Suy ra, giá trị cực tiểu luôn nhỏ hơn 0 với mọi m.

Dựa vào bảng biến thiên suy ra đường thẳng y = 0 (trục hoành) luôn cắt đồ thị hàm số tại 2 điểm phân biệt (đpcm).

...

Nội dung giải bài tập còn tiếp, mời các em xem full tại file tải về miễn phí...

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về ĐẦY ĐỦ hướng dẫn giải bài tập Toán 12 Ôn tập chương 1 file Word, pdf hoàn toàn miễn phí!