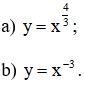Giải bài tập Toán 12 Bài 2: Hàm số lũy thừa

Nội dung hướng dẫn giải được chúng tôi trình bày chi tiết, rõ ràng bám sát nội dung SGK Toán Giải tích lớp 12 Bài 2: Hàm số lũy thừa. Chia sẻ đến các em phương pháp giải hay, dễ hiểu, giúp các em hiểu sâu và ứng dụng kiến thức đã học trên lớp vào các dạng bài tập phần hàm số lũy thừa.

Giải Toán 12 chương 2 bài 2: Hàm số lũy thừa

Trả lời câu hỏi SGK Toán Giải tích 12 Bài 2 (Chương 2):

Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 57: 

Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng: y = x^2, y = x^(1/2), y = x^(-1).

Lời giải:

Đồ thị của hàm số y = x²: đường màu đỏ.

Đồ thị của hàm số y = x^(1/2): đường màu xanh.

Đồ thị của hàm số y = x^(-1) đường màu tím.

Ta có:

Tập xác định của hàm số y = x² là R.

Tập xác định của hàm số y = x^(1/2) là [0,+∞).

Tập xác định của hàm số y = x^(-1)là R\{0}.

Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 57: Tính đạo hàm của các hàm số:

Lời giải:

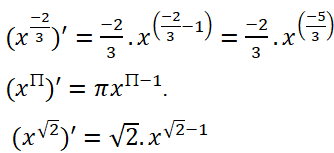
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 58: 

Tính đạo hàm của hàm số y = (3x² – 1)^(-√2).

Lời giải:

y’= [(3x² – 1)^(-√2)]'

= -√2.(3x² – 1)^(-√2-1).(3x² – 1)'

= -√2.(3x² – 1)^(-√2-1).6x

= -6√2 x.(3x² – 1)^(-√2-1).

Giải bài tập SGK Toán Giải tích 12 Bài 2 (Chương 2):

Bài 1 (trang 60 SGK Giải tích 12): 

Tìm tập xác định của các hàm số:

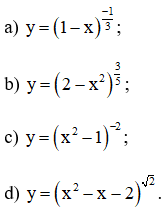
Lời giải:

a) Hàm số y = (1 - x)^(-1/3) xác định

⇔ 1 – x > 0

⇔ x < 1.

Vậy tập xác định D = (-∞; 1).

b) Hàm số y = (2 - x²)^(3/5) xác định

⇔ 2 – x² > 0

⇔ x² < 2

⇔ -√2 < x < √2.

Vậy tập xác định D = (-√2; √2).

c) Hàm số y = (x² – 1)^-2 xác định khi và chỉ khi:

x² - 1 ≠ 0 ⇔ x² ≠ 1 ⇔ x ≠ ±1

Vậy tập xác định của hàm số là D = R\ {-1; 1}.

d) 

⇔ x² – x – 2 > 0

⇔ (x + 1)(x – 2) > 0

⇔ x < -1 hoặc x > 2

Vậy tập xác định D = (-∞; -1) ∪ (2; +∞).

Bài 2 (trang 61 SGK Giải tích 12): 

Tính đạo hàm của các hàm số:

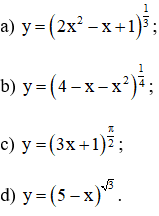
Lời giải:

 

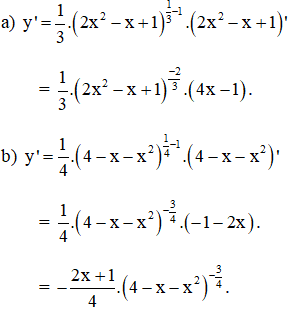
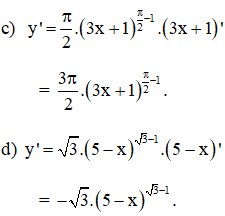
Bài 3 (trang 61 SGK Giải tích 12): 

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:

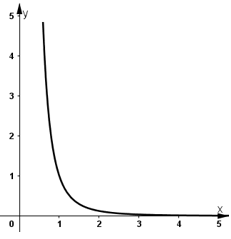
b) y = x^-3

Lời giải:

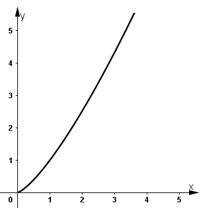
a) Xét hàm số y = x^4/3 ta có:

- Tập khảo sát : (0 ; +∞).

- Sự biến thiên:

+ 

với ∀ x > 0.

Do đó, hàm số đã cho đồng biến trên tập xác định.

+ Giới hạn:

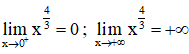
+ Tiệm cận : Đồ thị hàm số không có tiệm cận.

+ Bảng biến thiên:

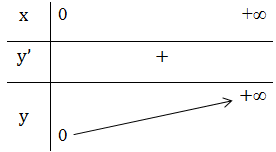
- Đồ thị hàm số:

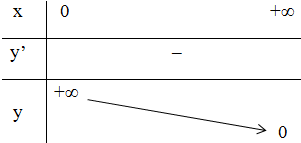
b) Xét hàm số y = x^-3, ta có :

- Tập khảo sát : (0 ; +∞).

- Sự biến thiên:

+ y' = -3.x^{-3 - 1} = -3.x^-4 < 0 với ∀ x > 0.

Do đó, hàm số đã cho nghịch biến trên tập xác định.

+ Giới hạn:

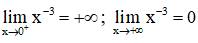
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số

    y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.

+ Bảng biến thiên:

- Đồ thị:

Bài 4 (trang 61 SGK Giải tích 12): 

Hãy so sánh các số sau với 1:

a) (4,1)^2,7;

b) (0,2)^0,3;

c) (0,7)^3,2;

d) (√3)^0,4

Lời giải:

a) Cách 1. Ta có: 2,7 > 0 nên hàm y = x^2,7 luôn đồng biến trên (0 ; +∞).

Vì 4,1 > 1 ⇒ (4,1)^2,7 > 1^2,7 = 1.

Cách 2. Ta có 4,1 > 1 và 2,7 > 0 nên ta có :

(4,1)^2,7 > (4,1)⁰ hay (4,1)^2,7 > 1

b) Ta có : 0,3 > 0 nên hàm số y = x^0,3 đồng biến trên (0 ; +∞).

Vì 0,2 < 1 ⇒ 0,2^0,3 < 1^0,3 = 1.

c) Ta có: 3,2 > 0 nên hàm số y = x^3,2 đồng biến trên (0 ; +∞)

Vì 0,7 < 1 ⇒ 0,7^3,2 < 1^3,2 = 1.

d) Ta có: 0,4 > 0 nên hàm số y = x^0,4 đồng biến trên (0 ; +∞)

Vì √3 > 1 ⇒ (√3)^0,4 > 1^0,4 = 1.

Bài 5 (trang 61 SGK Giải tích 12): 

So sánh

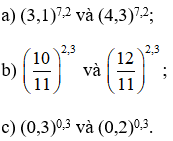
Lời giải:

Hàm số y = x^α luôn đồng biến trên (0 ; +∞) với α > 0

a) Ta có : 7,2 > 0

Vì 3,1 < 4,3 nên (3,1)^7,2 < (4,3)^7,2.

b) Ta có : 2,3 > 0

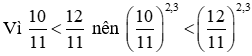
c) Ta có : 0,3 > 0

Vì 0,3 > 0,2 nên (0,3)^0,3 > (0,2)^0,3.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập SGK Toán 12 Bài 2: Hàm số lũy thừa file Word, pdf hoàn toàn miễn phí!