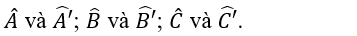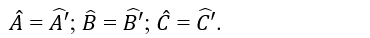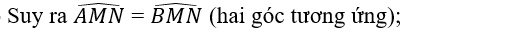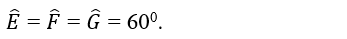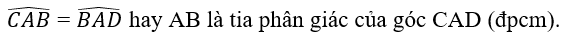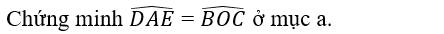Giải Toán lớp 7 VNEN Bài 2: Trường hợp bằng nhau cạnh-cạnh-cạnh

Hướng dẫn Giải bài tập Toán VNEN Bài 1: Hai tam giác bằng nhau trang 115 đến 119 Hình học Tập 1 chương 2 sách giáo khoa lớp 7 chương trình mới chính xác, ngắn gọn và dễ hiểu dưới đây sẽ giúp các em học sinh trả lời các câu hỏi và giải các bài toán nhanh chóng, tiếp thu bài học trên lớp tốt hơn.

A. Hoạt động khởi động Bài 1: Hai tam giác bằng nhau

Thực hiện các hoạt động sau

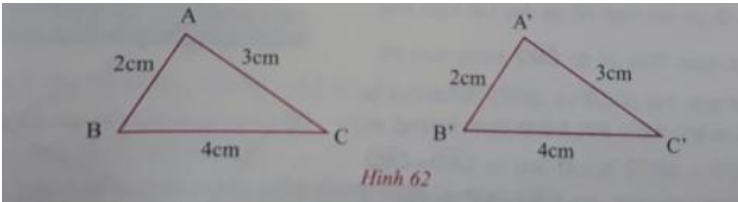
a) Vẽ vào vở các tam giác △ABC và △A′B′C′ thỏa mãn AB = A’B’ = 2 cm; AC = A’C’ = 3 cm; BC = B’C’ = 4 cm (h.62).

c) Hai tam giác ABC và A’B’C’ có bằng nhau hay không? Vì sao?

Lời giải:

a) Các em thực hiện vẽ hai tam giác ABC và A’B’C’ với độ dài các cạnh đã cho như hình 62.

b) Thực hiện phép đo góc, ta có:

c) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh tương ứng và các góc tương ứng bằng nhau.

B. Hoạt động hình thành kiến thức Bài 1: Hai tam giác bằng nhau

Câu 1: (trang 115 SGK Toán lớp 7 VNEN tập 1 chương 2)

Đọc kĩ nội dung sau (Sgk)

Câu 2: (trang 116 SGK VNEN Toán 7 tập 1 chương 2)

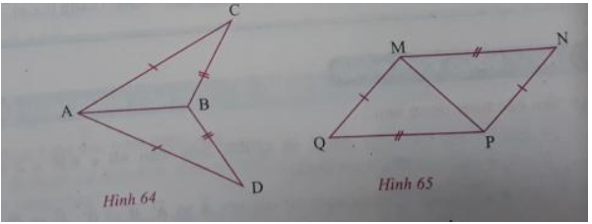
a) Quan sát các hình 64 và 65. Hãy kí hiệu thể hiện sự bằng nhau của các tam giác có trong mỗi hình vẽ đó. Giải thích vì sao?

b) Quan sát hình 66 và đọc bài toán sau (Sgk trang 116)

Câu 3: (trang 116 SGK Toán VNEN lớp 7 tập 1 chương 2)

a) Bằng compa và thước thẳng, hãy vẽ tia phân giác của một góc cho trước (sgk trang 116)

b) Đọc kĩ nội dung sau (sgk trang 117)

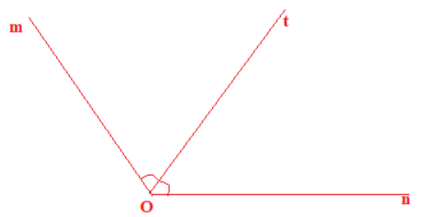
c) Vẽ tia phân giác của góc mOn trên hình 68.

Lời giải:

c) Thực hiện các bước vẽ tia phân giác của một góc bằng thước thẳng và compa, ta được tia Ot là tia phân giác của góc mOn (hình vẽ).

C. Hoạt động luyện tập Bài 1: Hai tam giác bằng nhau

Câu 1: (trang 117 SGK Toán 7 VNEN tập 1 chương 2)

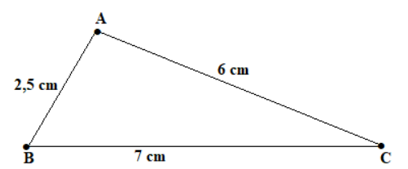
a) Vẽ vào vở tam giác △ABC biết AB = 2,5 cm; AC = 6 cm; BC = 7 cm.

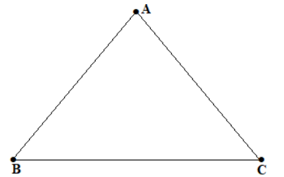
b) Vẽ vào vở tam giác △EFG có EF = FG = GE = 3cm. Sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc.

c) Sắp xếp trình tự các bước chứng minh bài toán sau

Bài toán: “△AMB và △ANB có MA = Mb, NA = NB (h.69). Chứng minh rằng

Các bước chứng minh:

i) Do đó △AMN=△BMN (c.c.c).

ii) MN: cạnh chung;

MA = MB (giả thiết);

NA = NB (giả thiết);

iii)

iv) △AMN và △BMN.

Lời giải:

a) Các em thực hiện các bước vẽ tam giác khi biết 3 cạnh bằng thước thẳng và compa vào vở.

b) Các em thực hiện các bước vẽ tam giác khi biết 3 cạnh bằng thước thẳng và compa vào vở.

Thực hiện đo các góc của tam giác EFG, ta có:

Câu 2: (trang 118 SGK VNEN Toán lớp 7 tập 1 chương 2)

a) Ví dụ (sgk trang 118)

b) Em hãy giải bài toán sau vào vở như ví dụ trên.

Bài toán: Cho đoạn thẳng AB = 5 cm. Vẽ đường tròn tâm A bán kính 3 cm và đường tròn tâm B bán kính 4,5 cm chúng cắt nhau ở C và D. Chứng minh AB là tia phân giác của góc CAD.

Lời giải:

Xét △ABC và △ABD có:

AB: chung;

AC = AD = 3 cm (bán kính đường tròn tâm A);

BC = BD = 4,5 cm (bán kính đường tròn tâm B);

Vậy: △ABC=△ABD

Suy ra:

D. Hoạt động vận dụng Bài 1: Hai tam giác bằng nhau

Câu 1: (trang 118 SGK Toán VNEN 7 tập 1 chương 2)

a) Vẽ một góc cho trước (sgk trang 118)

b)

Lời giải:

b) Xét △OBC và △ADE có:

OB = AD = r (các cung tròn cùng bán kính, theo cách dựng);

OC = AE = r (các cung tròn cùng bán kính, theo cách dựng);

BC = DE (theo cách dựng);

Vậy: △OBC=△ADE.

 

Câu 2: (trang 119 SGK Toán lớp 7 VNEN tập 1 chương 2)

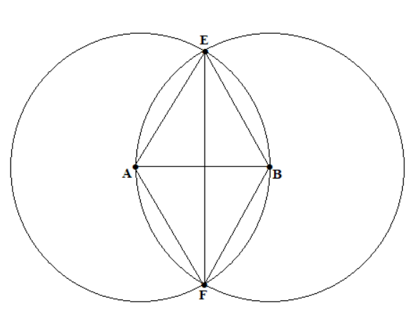
Cho hai điểm A và B phân biệt. Vẽ cung trong tâm A bán kính AB và cung tròn tâm B bán kính BA, hai cung tròn cắt nhau tại E và F.

Chứng minh rằng:

a) △ABE = △ABF;

b) △AEF = △BEF;

c) AE // BF; AF // BE.

Lời giải:

a) Xét △ABE và △ABF có:

AB: chung;

AE = AF (bán kính đường tròn tâm A);

BE = BF (bán kính đường tròn tâm B);

Vậy: △ABE = △ABF (đpcm).

b) Xét △AEF và △BEF có:

EF: chung;

AE = BE = AB (hai đường tròn cùng bán kính);

AF = BF (hai đường tròn cùng bán kính);

Vậy: △AEF=△BEF (đpcm).

c)

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán 7 VNEN Bài 2: Trường hợp bằng nhau cạnh-cạnh-cạnh file PDF hoàn toàn miễn phí.