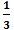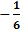Giải Toán lớp 7 VNEN Bài 9: Ôn tập chương 4
Hướng dẫn Giải bài tập Toán VNEN Bài 9: Ôn tập chương 4 trang 58 đến 61 Đại số Tập 2 chương 4 sách giáo khoa lớp 7 chương trình mới chính xác, ngắn gọn và dễ hiểu dưới đây sẽ giúp các em học sinh trả lời các câu hỏi và giải các bài toán nhanh chóng, tiếp thu bài học trên lớp tốt hơn.
C. Hoạt động luyện tập Bài 9: Ôn tập chương 4
Trả lời các câu hỏi sau
a) Viết năm đơn thức của hai biến x, y trong đó x và y có bậc khác nhau. Chỉ rõ hệ số và bậc của mỗi đơn thức đó.
b) Thế nào là hai đơn thức đồng dạng? Cho ví dụ;
c) Nêu cách để cộng, trừ hai đơn thức đồng dạng;
d) Thế nào là đa thức? Viết một đa thức nhưng không phải là đơn thức. Chỉ rõ bậc của đa thức đó;
e) Viết đa thức một biến có hệ số cao nhất bằng 10, hệ số tự do bằng -1;
f) Khi nào số a được gọi là nghiệm của đa thức P(x)?
Trả lời:
a) - Đơn thức: x4y với hệ số là 1 và bậc là 5;
- Đơn thức: 2x2y với hệ số là 2 và bậc là 3;
- Đơn thức: 3 x3y với hệ số là 3 và bậc là 4;
- Đơn thức: 4 xy3 với hệ số là 4 và bậc là 4 ;
- Đơn thức: 5x10y với hệ số là 5 và bậc là 11;
b) Hai dơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Ví dụ: 2x2y và -7x2y là hai đơn thức đồng dạng.
c) Để cộng (hay trừ) hai đơn thức đồng dạng, ta cộng (hay trừ) hai hệ số với nhau và giữ nguyên phần biến.
d) Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng được gọi là một hạng tử của đa thức đó.
Ví dụ: M(x) = 2x2 – xy + 1
Ta nói bậc của đa thức M(x) là 2
e) Đa thức một biến có hệ số cao nhất bằng 10, hệ số tự do bằng - 1 là: 10x2 + x – 1
f) Số a được gọi là nghiệm của đa thức P(x) khi tại x = a, giá trị của đa thức P(x) bằng 0.
Làm các bài tập sau:
Câu 1. (trang 59 SGK Toán lớp 7 VNEN chương 4 tập 2)
Hãy viết biểu thức diễn đạt các ý sau:
a) Hiệu các bình phương của hai số a và b;
b) Tổng các bình phương của hai số x, y nhân với hai lần tích của hai số đó;
c) Lập phương của hiệu hai số m và n chia cho 2015
Trả lời:
a) a2 – b2
b, (x2 + y2).2xy
c) (m – n )3 : 2015
Câu 2. (trang 59 SGK Toán VNEN lớp 7 chương 4 tập 2)
Viết một biểu thức đại số của hai biến x, y trong từng trường hợp sau:
a) Biểu thức đó là đơn thức;
b) Biểu thức đó là đa thức nhưng không phải là đơn thức.
Trả lời:
a) 172xy;
b) T = x2 + y2 + 2xy +34
Câu 3. (trang 59 SGK VNEN Toán 7 chương 4 tập 2)
Tính giá trị của mỗi biểu thức sau tại x = 1; y= -1 và z = -2:
a) 2xy(5x2y + 3x - z); b) xy2 + y2z3 + z3x4
Trả lời:
a) Thay x = 1; y = -1 và z = -2 vào biểu thức 2xy(5x2y + 3x - z) ta có:
2(1)(-1)[5(1)2(-1) + 3(1) - (-2)] = 0
b) Thay x = 1; y = -1 và z = -2 vào biểu thức xy2 + y2z3 + z3x4 ta có:
(1)(-1)2 + (-1)2(-2)3 + (-2)3(1)4 = - 15
Câu 4. (trang 59 SGK Toán VNEN 7 chương 4 tập 2)
Hãy điền thêm một đơn thức vào ô trống (...) để tích của hai đơn thức ở hai ô liền nhau là một đơn thức đồng dạng với đơn thức ở ô tương ứng:
Trả lời:
Câu 5. (trang 59 SGK Toán 7 VNEN chương 4 tập 2)
Hãy viết các đơn thức đồng dạng với đơn thức xy2 sao cho tại x = 1 và y = - 1, giá trị của các đơn thức đó là số tự nhiên nhỏ hơn 7.
Trả lời:
Các đơn thức đồng dạng với đơn thức xy2 sao cho tại x = 1 và y = - 1, giá trị của các đơn thức đó là số tự nhiên nhỏ hơn 7 bao gồm:
3xy2; 4xy2; 5xy2; 6xy2 và 2xy2
Câu 6. (trang 59 SGK VNEN Toán lớp 7 chương 4 tập 2)
Tính tích của các đơn thức trong mỗi trường hợp sau
rồi tìm hệ số và bậc của tích tìm được.
a) 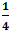
Trả lời:
a) Ta có: ( 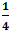
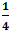
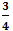
Hệ số của tích vừa tìm được là −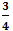
b) Ta có: (- 2x2yz3).(- 5x3y3z) = (- 2).(-5).x2.x3.y.y3.z3.z = 10x5y4z4
Hệ số của tích vừa tìm được là 10 và bậc là 13.
Câu 7. (trang 60 SGK Toán VNEN 7 chương 4 tập 2)
Cho hai đa thức:
P(x) = x5 – 3x2 + 7x4 – 9x3 + x2 –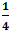
Và Q(x) = 5x4 – x5 + x2 – 2x3 + 3x2 –
a) Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dàn của biến.
b) Tính P(x) + Q(x) và P(x) – Q(x)
c) Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x).
Trả lời:
a) - Rút gọn đa thức P(x) ta được: P(x) = x5 – 2x2 + 7x4 – 9x3 –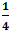
Sắp xếp hạng tử theo lũy thừa giảm dần của biến ta được:
P(x) = x5 + 7x4 – 9x3 – 2x2 – 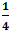
- Rút gọn đa thức Q(x) ta được: Q(x) = 5x4 – x5 – 2x3 + 4x2 –
Sắp xếp hạng tử theo lũy thừa giảm dần của biến ta được:
Q(x) = – x5 + 5x4– 2x3 + 4x2 –
b) Ta có:
- P(x) + Q(x) = (x5 – 3x2 + 7x4 – 9x3 + x2 –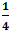
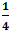
= (x5 – x5) + (7x4 + 5x4) – (9x3 + 2x3) – (3x2 – x2 – x2 – 3x2)
= 12 x4 – 11x3 + 2x2
- P(x) – Q(x) = (x5 – 3x2 + 7x4 – 9x3 + x2 – 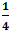
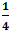
= x5 – 3x2 + 7x4 – 9x3 + x2 – 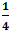
= (x5 + x5) + (7x4 – 5x4) – (9x3 – 2x3) – (3x2 – x2 + x2 + 3x2)
= 2x5 + 2 x4 – 7x3 – 6x2
c) - Tại x = 0, giá trị của đa thức P(x) là:
P(0) = (0)5 – 3(0)2 + 7(0)4 – 9(0)3 + (0)2 – 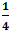
- Tại x = 0, giá trị của đa thức Q(x) là:
Q(0) = 5(0)4 – (0)5 + (0)2 – 2(0)3 + 3(0)2 - 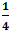
Vậy x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x)
Câu 8. (trang 60 SGK VNEN Toán 7 chương 4 tập 2)
Cho đa thức:
M(x) = 5x3 +2x4 – x2 + 3x2 – x3 – x4 + 1 – 4x3
a) Sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
b) Tính M(1) và M(-1)
c) Chứng tỏ rằng đa thức trên không có nghiệm.
Trả lời:
a) Sắp xếp: M(x) = 2x4 – x4 – x3 – 4x3 +5x3 – x2 + 3x2 + 1
b) Ta có:
- M(1) = 5(1)3 +2(1)4 – (1)2 + 3(1)2 – (1)3 – (1)4 + 1 – 4(1)3 = 4
- M(-1) = 5(-1)3 +2(-1)4 – (-1)2 + 3(-1)2 – (-1)3 – (-1)4 + 1 – 4(-1)3 = -4
c) Ta có: M(x) = 5x3 +2x4 – x2 + 3x2 – x4 – x3 + 1 – 4x3
= (5x3 – x3 – 4x3) +(2x4 – x4) – (x2 – 3x2) + 1
= x4 + 2x2 + 1 = (x2 + 1)2
Tại x = a bất kỳ, ta luôn có: M(a) = (a2 + 1)2 > 0 (đpcm)
Vậy không tồn tại bất kỳ giá trị x nào để giá trị của đa thức M(x) = 0. Hay nói cách khác, đa thức M(x) vô nghiệm.
Câu 9. (trang 60 SGK Toán 7 VNEN chương 4 tập 2)
Khoanh vào số được cho ở cột bên phải, mà nó là nghiệm của đa thức được cho ở cột bên trái, cùng hàng, trong bảng sau.
| Đa thức | Các số tương ứng |
|---|---|
| a) A(x) = 3x – 6 | -2 0 2 3 |
| b) B(x) = 3x + | - |
| c) M(x) = x2 – 3x + 2 | -2 -1 1 2 |
| d) P(x) = x2 + 5x – 6 | -6 -1 1 6 |
| e) Q(x) = x2 + x | -1 0 |
Trả lời:
a) Khoanh: 2
b) Khoanh:
c) Khoanh: 1 và 2
d) Khoanh: - 6 và 1
e) Khoanh: -1 và 0
D. Hoạt động vận dụng Bài 9: Ôn tập chương 4
Trang 60 SGK Toán lớp 7 VNEN chương 4 tập 2
Olympic Tiếng Anh trên mạng là cuộc thi yêu thích của Huy. Huy đang tham gia vòng thì tự luyện. Trong một vòng thi, bạn ấy đã dành:
- x phút để làm bài thi thứ nhất;
- Nhiều hơn 1 phút so với thời gian làm bài thi thứ nhất để làm bài thi thứ hai;
- Hai lần thời gian làm bài thi thứ hai để làm bài thi thứ ba;
- Ít hơn 1 phút so với thời gian làm bài thi thứ ba để làm bài thi thứ tư.
a) Viết theo x thời gian để Huy làm bài thi thứ ba trong vòng thi.
b) Viết theo x tổng thời gian Huy đã làm cả vòng thi đó.
c) Huy đã mất 16 phút để tự hiện vòng thi đó. Hỏi Huy đã mất bao nhiêu phút để làm bài thi thứ tư?
Trả lời:
a) Thời gian để Huy làm bài thi thứ hai trong vòng thi là: x + 1 phút
Suy ra, thời gian để Huy làm bài thi thứ ba là: 2(x +1) phút
b) Thời gian để Huy làm bài thi thứ tư là: 2(x + 1) – 1 phút
Suy ra, tổng thời gian Huy đã làm cả vòng thi đó (chính là tổng thời gian của bốn bài thi)
là: x + (x + 1) + 2(x + 1) + 2(x + 1) – 1 = 6x + 4 phút
c) Theo giả thiết, Huy đã mất 16 phút để thực hiện vòng thi và từ kết quả của câu (b) ta
có: 6x + 4 = 16 ⇒ x = 2
Suy ra, thời gian để Huy làm bài thi thứ 4 là: 2(2 +1) – 1 = 5 phút
E. Hoạt động tìm tòi mở rộng Bài 9: Ôn tập chương 4
Câu 1. (trang 61 chương 4 tập 2 SGK Toán 7 VNEN)
Đố em tìm được một số thỏa mãn mỗi trường hợp sau đây:
a) Bình phương của nó bằng chính nó;
b) Lập phương của nó bằng chính nó
Trả lời:
a) Số 1 có bình phương của nó bằng chính nó: (1)2 = 1
b) Số 1 có lập phương của nó bằng chính nó: (1)3 = 1
Câu 2. (trang 61 chương 4 tập 2 SGK Toán VNEN lớp 7)
Quan sát các mô hình của các chữ số được làm từ các đoạn thẳng có chiều dài bằng nhau (que diêm, ghim nhọn, …). Bạn sẽ tìm thấy chữ số phân đoạn như bên màn hình của chiếc đồng hồ điện tử hay máy tính (h.8).
Nếu số lượng các chữ số được hình thành là n, số lượng đoạn thẳng cần thiết để hình thành n chữ số đó được cho bởi biểu thức đại số ở bên phải của mỗi mẫu.
Tính số đoạn thẳng để tạo thành 5, 10, 100 chữ số của các loại: 6, 4, 8 (h.8)
Trả lời:
- Để hình thành 5 chữ số 6 cần số đoạn thẳng là: 5.5 + 1 = 26
Để hình thành 10 chữ số 6 cần số đoạn thẳng là: 5.10 + 1 = 51
Để hình thành 100 chữ số 6 cần số đoạn thẳng là: 5.100 +1 = 501
- Để hình thành 5 chữ số 4 cần số đoạn thẳng là: 3.5 +1 = 16
Để hình thành 10 chữ số 4 cần số đoạn thẳng là: 3.10 + 1 = 31
Để hình thành 100 chữ số 4 cần số đoạn thẳng là: 3.100 + 1 = 301
- Để hình thành 5 chữ số 8 cần số đoạn thẳng là: 5.5 + 2 = 27
Để hình thành 10 chữ số 8 cần số đoạn thẳng là: 5.10 + 2 = 52
Để hình thành 100 chữ số 8 cần số đoạn thẳng là: 5.100 + 2 = 502
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán 7 VNEN Bài 9: Ôn tập chương 4 file PDF hoàn toàn miễn phí.
- Giải Toán lớp 7 VNEN Bài 1: Biểu thức đại số, giá trị của một biểu thức đại số
- Giải Toán lớp 7 VNEN Bài 4: Trung bình cộng, mốt
- Giải Toán lớp 7 VNEN Bài 8: Nghiệm của đa thức một biến
- Giải Toán lớp 7 VNEN Bài 5: Cộng, trừ đa thức
- Giải Toán lớp 7 VNEN Bài 5: Ôn tập chương 3
- Giải Toán lớp 7 VNEN Bài 6: Đa thức một biến
- Giải Toán lớp 7 VNEN Bài 7: Cộng, trừ đa thức một biến
- Giải Toán lớp 7 VNEN Bài 4: Đa thức chính xác


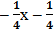
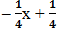
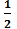
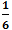 -
-