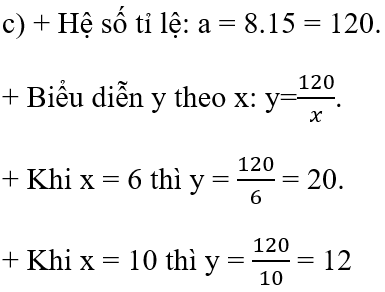Giải Toán lớp 7 VNEN Bài 3: Đại lượng tỉ lệ nghịch
Hướng dẫn Giải bài tập Toán VNEN Bài 3: Đại lượng tỉ lệ nghịch trang 58 đến 60 Đại số Tập 1 chương 2 sách giáo khoa lớp 7 chương trình mới chính xác, ngắn gọn và dễ hiểu dưới đây sẽ giúp các em học sinh trả lời các câu hỏi và giải các bài toán nhanh chóng, tiếp thu bài học trên lớp tốt hơn.
A. Hoạt động khởi động Bài 3: Đại lượng tỉ lệ nghịch
Câu 1: (trang 58 SGK Toán lớp 7 VNEN tập 1 chương 2)
a) Đọc rồi ghi kết quả vào bảng sau:
Có 100 kg gạo được chia đều vào các bao. Hãy cho biết số bao gạo có được sau khi chia hết số gạo đó vào các bao, mỗi bao đựng 5 kg, 10 kg, 20 kg, 25 kg, 50 kg.
| Số kilogam gạo ở mỗi bao | 5 kg | 10 kg | 20 kg | 25 kg | 50 kg |
| Số bao gạo | 20 bao | ... bao | ... bao | ... bao | ... bao |
b) Nêu nhận xét về mối quan hệ giữa số kilogam gạo ở mỗi bao và số bao gạo cần để đựng.
Lời giải:
a)
| Số kilogam gạo ở mỗi bao | 5 kg | 10 kg | 20 kg | 25 kg | 50 kg |
| Số bao gạo | 20 bao | 10 bao | 5 bao | 4 bao | 2 bao |
b) Nhận xét: Số kilogam gạo ở mỗi bao càng lớn thì số bao gạo cần để đựng càng nhiều.
Câu 2: (trang 58 SGK Toán lớp 7 VNEN tập 1 chương 2)
Nêu nhận xét về mối quan hệ giữa các đại lượng có trong các ví dụ dưới đây.
a) Vận tốc v (km/h) và thời gian t (h) của một vật chuyển động đều trên một quãng đường nhất định.
b) Tiền công được nhận sau khi hoàn thành một công việc và số người tham gia làm việc (với tổng mức khoán đã được cố định).
c) Chiều dài và chiều rộng của hình chữ nhật khi diện tích của hình chữ nhật là không đổi.
d) Chu vi và bán kính của một bánh xe.
Lời giải:
a) Khi vận tốc chuyển động của vật càng lớn thì thời gian chuyển động của vật càng nhỏ.
b) Nếu số lượng người tham gia công việc càng nhiều thì tiền công nhận được càng ít.
c) Khi diện tích của hình chữ nhật không thay đổi thì chiều dài càng lớn thì chiều rộng càng bé.
d) Bán kính của bánh xe càng lớn thì chu vi của bánh xe càng lớn.
B. Hoạt động hình thành kiến thức Bài 3: Đại lượng tỉ lệ nghịch
Câu 1: (trang 58 SGK Toán lớp 7 VNEN tập 1 chương 2)
a) Thực hiện các hoạt động sau
+ Viết công thức tính chiều dài y (cm) theo chiều rộng x (cm) của hình chữ nhật thay đổi nhưng luôn có diện tích bằng 12 (cm2).
+ Viết công thức tính lượng gạo y (kg) trong mỗi bao theo x khi chia đều 500 kg gạo vào x bao.
+ Nêu nhận xét về những điểm giống nhau trong các công thức trên.
b) Đọc kĩ nội dung sau (Sgk trang 58)
c) Cho biết đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ 3,5. Hỏi đại lượng x tỉ lệ nghịch với y theo hệ số tỉ lệ nào?
Lời giải:
a) + Biểu diễn mối liên hệ giữa chiều dài và chiều rộng của hình chữ nhật thay đổi nhưng luôn có diện tích bằng 12 (cm2): y = 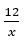
+ Biểu diễn mối liên hệ giữa lượng gạo trong mỗi bao khi chia đều 500 kg gạo vào các bao: y = 500x (kg).
+ Nhận xét: Các đại lượng đều được biểu diễn theo công thức có dạng: y = 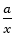
c) Đại lượng x tỉ lệ nghịch với y theo hệ số tỉ lệ: k = 3,5.
Câu 2: (trang 59 SGK Toán lớp 7 VNEN tập 1 chương 2)
a) Thực hiện các hoạt động sau
Cho biết đại lượng y và x tỉ lệ nghịch với nhau và một vài thông tin như trong bảng sau:
| x | x1 = 2 | x2 = 4 | x3 = 5 | x4 = 6 |
| y | y1 = 30 | y2 = ? | y3 = ? | y4 = ? |
+ Hãy xác định hệ số tỉ lệ của y đối với x.
+ Theo đó thay mỗi dấu “?” trong bảng trên bằng một số thích hợp.
+ Nêu nhận xét về tích hai giá trị tương ứng: x1.y1; x2.y2; x3.y3; x4.y4 của x và y.
b) Đọc kĩ nội dung sau (Sgk trang 59)
c) Thực hiện nhiệm vụ sau rồi chia sẻ với bạn
Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 8 thì y = 15.
+ Tìm hệ số tỉ lệ a của y đối với x.
+ Hãy biểu diễn y theo x.
+ Tính giá trị của y khi x = 6, x = 10.
Lời giải:
a) + Hệ số tỉ lệ: a=x1.y1=2.30=60a=x1.y1=2.30=60.
+ Ta có bảng sau:
| x | x1 = 2 | x2 = 4 | x3 = 5 | x4 = 6 |
| y | y1 = 30 | y2 = 15 | y3 = 12 | y4 = 10 |
+ Tích hai giá trị tương ứng: x1.y1=x2.y2=x3.y3=x4.y4=60x1.y1=x2.y2=x3.y3=x4.y4=60.
C. Hoạt động luyện tập Bài 3: Đại lượng tỉ lệ nghịch
Câu 1: (trang 59 SGK Toán lớp 7 VNEN tập 1 chương 2)
a) Điền số thích hợp vào ô trống trong bảng sau:
(1) Hình chữ nhật có diện tích là 60 (cm2):
| Chiều rộng (cm) | 2 | 3 | 4 | 5 | 6 |
| Chiều dài (cm) |
(2) Hình chữ nhật có chu vi 26 cm:
| Chiều rộng (cm) | 2 | 3 | 4 | 5 | 6 |
| Chiều dài (cm) |
(2) Hình c
(3) Cho biết 35 công nhân xây xong một ngôi nhà hết 168 ngày (mỗi ngày làm việc 8 giờ), năng suất lao động của các công nhân là như nhau.
| Số công nhân (người) | 7 | 8 | 20 | 21 | 28 |
| Thời gian xây (ngày) |
(2) Hình c
b) Các đại lượng nêu trong mỗi bảng trên có tỉ lệ nghịch với nhau hay không?
c) Tìm công thức biểu thị liên hệ giữa các đại lượng tỉ lệ nghịch đó và chỉ ra hệ số tỉ lệ
Lời giải:
a) (1) Hình chữ nhật có diện tích là 60 (cm2):
| Chiều rộng (cm) | 2 | 3 | 4 | 5 | 6 |
| Chiều dài (cm) | 30 | 20 | 15 | 12 | 10 |
(2) Hình chữ nhật có chu vi 26 cm:
| Chiều rộng (cm) | 2 | 3 | 4 | 5 | 6 |
| Chiều dài (cm) | 11 | 10 | 9 | 8 | 7 |
(3) Thời gian xây dựng nhà:
Năng suất lao động của mỗi công nhân trong một ngày là:
| Số công nhân (người) | 7 | 8 | 20 | 21 | 28 |
| Thời gian xây (ngày) | 840 | 735 | 294 | 280 | 210 |
b) Xét các tích số tương ứng:
(1) Hình chữ nhật có diện tích là 60 (cm2)
2.30 = 3.20 = 4.15 = 5.12 = 6.10 = 60
⇒ Chiều dài và chiều rộng của hình chữ nhật có diện tích là 60 (cm2) tỉ lệ nghịch với nhau.
(2) Hình chữ nhật có chu vi 26 cm.
2.11 ≠ 3.10 ⇒ Chiều dài và chiều rộng của hình chữ nhật có chu vi là 26 (cm) không tỉ lệ nghịch với nhau.
(3) Thời gian xây dựng nhà:
7.840 = 8.735 = 20.294 = 21.280 = 28.210 = 5880
⇒ Số công nhân và thời gian xây tỉ lệ nghịch với nhau.
c)
+ Mối liên hệ giữa chiều dài a và chiều rộng b của hình chữ nhật có diện tích 60 (cm2) là: a = 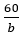
+ Mối liên hệ giữa số công nhân x và thời gian xây y là: y = 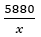
Câu 2: (trang 60 SGK Toán lớp 7 VNEN tập 1 chương 2). Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền số thích hợp vào ô trống trong bảng sau:
Lời giải:
+ Hai đại lượng x và y tỉ lệ nghịch với nhau, khi x = -8 thì y = 1,6
⇒ hệ số tỉ lệ là a = (-8).1,6 = - 12,8.
+ Ta có bảng đầy đủ như sau:
Câu 3: (trang 60 SGK Toán lớp 7 VNEN tập 1 chương 2)
Một xưởng may có 56 công nhân đang hoàn thành một hợp đồng may quần áo trong 21 ngày. Hỏi cần phải tăng thêm bao nhiêu công nhân nữa để có thể hoàn thành công việc đó trong 14 ngày, biết rằng năng suất lao động của các công nhân là như nhau?
Lời giải:
Nhận xét: Số công nhân và số ngày hoàn thành hợp đồng may là hai đại lượng tỉ lệ nghịch với nhau.
Gọi x (người) là số công nhân cần thiết để hoàn thành hợp đồng may trong 14 ngày.
Theo tính chất của hai đại lượng tỉ lệ nghịch với nhau, ta có:
14.x=21.56 ⇒ x = 21.56/14 = 84 (người).
Vậy số công nhân cần phải tăng thêm là: x–56=28 (công nhân).
D.E. Hoạt động vận dụng & Tìm tòi mở rộng Bài 3: Đại lượng tỉ lệ nghịch
Câu 1: (trang 60 SGK Toán lớp 7 VNEN tập 1 chương 2)
Trung bình 8 người gặt bằng tay, gặt xong một cánh đồng lúa trong 4 ngày (mỗi ngày 8 giờ). Một máy gặt đập liên hợp có công suất tương đương 128 người gặt. Hỏi máy gặt đập liên hợp gặt hết cánh đồng đó trong bao lâu?
Lời giải:
Đổi: 4 ngày làm việc = 32 giờ làm việc
Số người gặt x và thời gian gặt xong y là hai đại lượng tỉ lệ nghịch với nhau.
Hệ số tỉ lệ là: a=8.32=256.
Máy gặt đập liên hợp có năng suất tương đương 128 người gặt, nên thời gian làm việc của máy gặt đập liên hợp là:
128.x = a = 256 ⇒ x = 256:128 = 2 (giờ).
Câu 2: (trang 60 SGK Toán lớp 7 VNEN tập 1 chương 2)
Từ hộp thư điện tử Gmail, An có thể tải xuống các tài liệu với tốc độ tối đa là 0,5 Mb/s. Khi An tải xuống nhiều tài liệu cùng một lúc thì tốc độ tải xuống cho mỗi tài liệu sẽ bằng tốc độ tối đa chia cho số lượng tài liệu, biết rằng các tài liệu có dung lượng như nhau.
Điền số thích hợp vào ô trống trong bảng sau:
Lời giải:
Số tài liệu cần tải xuống và tốc độ tải xuống là hai đại lượng tỉ lệ nghịch với nhau với hệ số tỉ lệ k = 0,5. Từ đó, ta có bảng đầy đủ sau:
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán 7 VNEN Bài 3: Đại lượng tỉ lệ nghịch file PDF hoàn toàn miễn phí.
- Giải Toán lớp 7 VNEN: Bài 1 Tập hợp Q các số hữu tỉ
- Giải Toán lớp 7 VNEN: Bài 4: Giá trị tuyệt đối của một số hữu tỉ
- Giải Toán lớp 7 VNEN: Bài 5: Cộng trừ nhân chia số thập phân
- Giải Toán lớp 7 VNEN Bài 6: Mặt phẳng tọa độ
- Giải Toán lớp 7 VNEN Bài 12: Số thực ngắn gọn
- Giải Toán lớp 7 VNEN: Bài 3: Nhân chia số hữu tỉ
- Giải Toán lớp 7 VNEN Bài 13: Ôn tập chương 1
- Giải Toán lớp 7 VNEN Bài 11: Số vô tỉ ngắn gọn